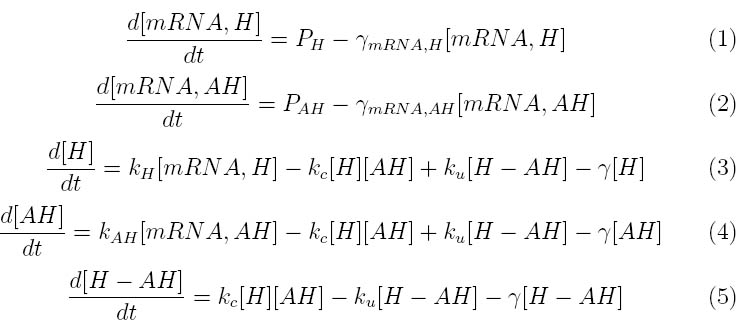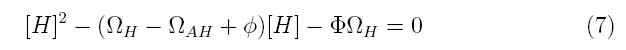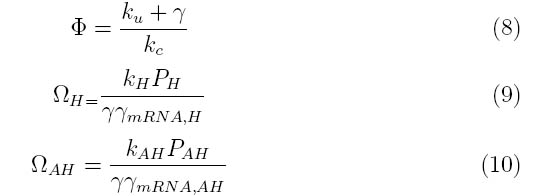Team:UC Berkeley/Modeling
From 2008.igem.org
Dirkvandepol (Talk | contribs) (→Introduction) |
Dirkvandepol (Talk | contribs) (→Transfer Function and Dimensionless Parameters) |
||
| Line 46: | Line 46: | ||
For example, Ω<sub>H</sub> consists of the rate constants for the formation of holin mRNA and the holin protein divided by their degradation rates. Strong promoters on holin will increase the value of Ω<sub>H</sub>, while high protein degradation rates will decrease Ω<sub>H</sub>. | For example, Ω<sub>H</sub> consists of the rate constants for the formation of holin mRNA and the holin protein divided by their degradation rates. Strong promoters on holin will increase the value of Ω<sub>H</sub>, while high protein degradation rates will decrease Ω<sub>H</sub>. | ||
| - | Ω<sub>AH</sub> describes the rate constants and degradation rates for | + | Ω<sub>AH</sub> describes the rate constants and degradation rates for antiholin. |
Φ describes the importance of the coupling and uncoupling rates of holin-antiholin dimer as well as the degradation rate of the dimer. | Φ describes the importance of the coupling and uncoupling rates of holin-antiholin dimer as well as the degradation rate of the dimer. | ||
Revision as of 02:43, 30 October 2008
Motivation
Since several phage systems and many promoters are currently in use, understanding the important parameters of the system allows one to choose appropriate promoters and phage proteins to optimize lysis behavior. Therefore we have created a model that is in agreement with our experimental results and published data regarding the T4 and λ phage systems.
Introduction
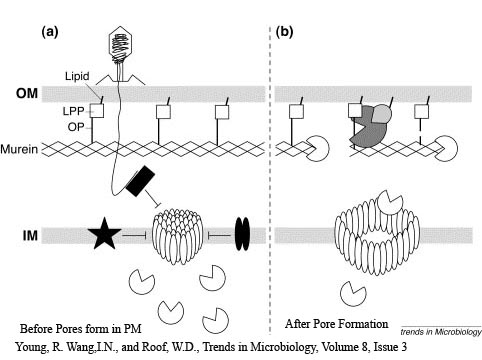
The holin-lysozyme phage lysis device consists of three proteins:
Holin - inner membrane-bound proteins that when complexed with other holin proteins, create holes in the membrane that allow lysozyme access to the periplasm.
Antiholin - inner membrane-bound protein that binds to and inactivates holin, producing an inactive holin-antiholin dimer. This dimer becomes active after holin forms enough pores in the plasma membrane to cause a loss of proton motive force between the periplasm and the cytosol.
Lysozyme - once holin forms pores in the inner membrane, lysozyme enters the periplasm and degrades peptidoglycan, resulting in cell lysis.
Governing Equations
Our holin-lysozyme lysis device consists of holin and lysozyme under an inducible promoter and antiholin under a constitutive promoter. For more information on our lysis device, click here [[1]].
The kinetics of our phage lysis device was modeled to help our team gain an insight into the behavior of our system. The below equations describe our system
Where PH represent the holin mRNA promoter strength as a function of arabinose concentration and PAH represents the antiholin mRNA promoter strength. γmRNA,H and γmRNA,AH represent the degradation rates for holin and antiholin respectively and γ represents the protein degradation rate. kH and kAH represent the rate constants for holin and antiholin formation. and kc and ku represent the coupling and uncoupling rates for the holin-antiholin dimer.
Transfer Function and Dimensionless Parameters
At steady state,
By making this assumption, the system of equations can be simplified into the following transfer function
Where the system can be divided into three dimensionless parameters which describe the behavior of the holin-antiholin dimer and the holin and antiholin proteins.
These dimensionless numbers can assist in the optimization of lysis device design because they describe the important parameters in the system.
For example, ΩH consists of the rate constants for the formation of holin mRNA and the holin protein divided by their degradation rates. Strong promoters on holin will increase the value of ΩH, while high protein degradation rates will decrease ΩH.
ΩAH describes the rate constants and degradation rates for antiholin.
Φ describes the importance of the coupling and uncoupling rates of holin-antiholin dimer as well as the degradation rate of the dimer.
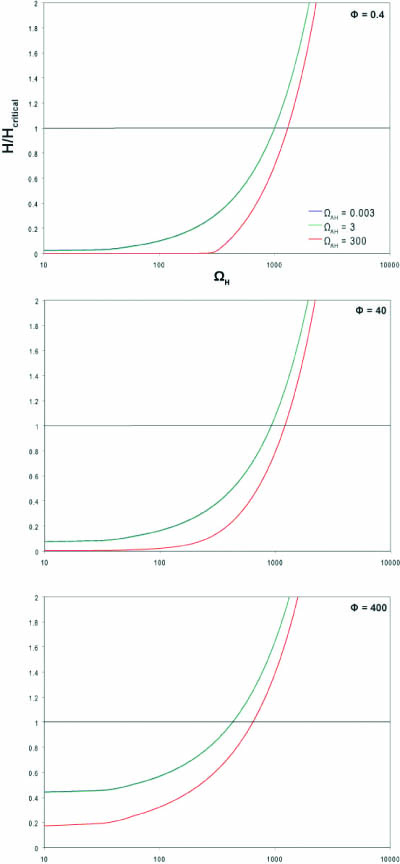
Graphs
Physiologically relevant values for ΩH, ΩAH and Φ were estimated based on rate constants for similar proteins. This system was input into MatLab to produce the following graph. Since there is a degree of uncertainty in these estimates, the graph spans several orders of magnitude above and below our estimated values. For the MatLab code used to produce these graphs, please click here Matlab code.
The literature indicates that at the time of lysis, cells infected with λ phage have approximately 1000 holin proteins1. Therefore, the critical concentration of holin (Hc) was set at 1000 holin proteins per cell.
The horizontal line at y=1 represents the critical holin concentration needed induce lysis. If the system produces more than the critical concentration of holin (>1000 free holin proteins), lysis is expected to occur.
As one would expect by looking at the dimensionless value for holin (omegaH), as the strength of the holin promoter increases, the amount of holin at steady state increases.
The graph also shows that the system is not very sensitive to small amounts of antiholin. Larger amounts of antiholin push the system equilibrium to the left and would require a stronger promoter on holin or a weaker binding interaction between holin and antiholin to reach critical concentration. This is supported by the observation that in a system with no antiholin, lysis can occur with holin under a weaker promoter.
Varying Φ, the dimensionless parameter that describes the coupling and uncoupling behavior of the holin-antiholin dimer, reveals that when the binding of holin-antiholin is stronger, a stronger promoter is required to reach the critical holin concentration.
Conclusions
There are several aspects of the model that agree with our experimental results and published data regarding phage lysis:
1. Our experimental results show that at higher concentrations of arabinose, lysis occurs more readily. In our model, higher concentrations of arabinose increase the value of PH and thus increase the value of omegaH. Our model predicts that as omegaH increases, lysis is more likely to occur.
2. Our experimental results showed that the T4 lysis device results in lysis at a lower concentration of arabinose than our λ lysis device when the systems are under the same promoter. λ antiholin and holin should have similar degradation rates because both are membrane-bound and only differ by two amino acids2. In contrast, T4 antiholin is an unstable cytoplasmic protein with a rapid degradation rate (t1/2 = 2 min)3. Therefore γ should be larger in the T4 system, resulting in a larger value for Φ. This will shift the graph up and allow the system to reach the critical holin concentration more readily (see graph with Φ =400).
3. Our model shows that systems with low values of omegaAH (weaker antiholin mRNA or protein promoter) will lyse more readily than systems with large values of omegaAH. This is in agreement with previously published results that show that in cells with little or no antiholin, lysis occurs more readily 2.
1. Christos G. Savva, Jill S. Dewey, John Deaton, Rebecca L. White, Douglas K. Struck, Andreas Holzenburg and Ry Young. The holin of bacteriophage lambda forms rings with large diameter. Molecular Microbiology 69(4), 784–793. 2008.
2. Martin Steiner and Udo Bläs. Charged amino-terminal amino acids affect the lethal capacity of Lambda lysis proteins S107 and S105. Molecular Microbiology. 8(3), 525 - 533. Oct. 2006.
3. Tram Anh T. Tran, Douglas K. Struck, and Ry Young*. The T4 RI Antiholin Has an N-Terminal Signal Anchor Release Domain That Targets It for Degradation by DegP. Journal of Bacteriology. 7618–7625. Nov. 2007.
 "
"