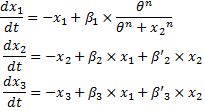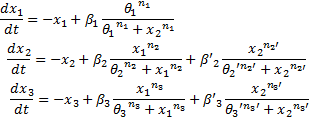Team:Paris/Modeling/BOB/Akaike
From 2008.igem.org
(Difference between revisions)
| Line 3: | Line 3: | ||
<center><html><div style="color:#275D96; font-size:2em;">Model Comparison</div></html></center> | <center><html><div style="color:#275D96; font-size:2em;">Model Comparison</div></html></center> | ||
| - | + | <br> | |
* Using linear equations in a biological system might seem awkards. However, we wanted to check the relevance of this approach. We have been looking for a criterium that would penalize a system that had many parameters, but that would also penalize a system which quadratic error would be too important while fitting experimental values. | * Using linear equations in a biological system might seem awkards. However, we wanted to check the relevance of this approach. We have been looking for a criterium that would penalize a system that had many parameters, but that would also penalize a system which quadratic error would be too important while fitting experimental values. | ||
* Akaike and Schwarz criteria taken from the information theory met our demands quite well : | * Akaike and Schwarz criteria taken from the information theory met our demands quite well : | ||
| Line 13: | Line 13: | ||
* It is remarquable that Akaike criterion and Hurvich and Tsai criterion are alike. AICc is therefore used for small sample size, but converges to AIC as n gets large. Since we will work with 20 points for each experiment, it seemed relevant to present both models. In addition, Schwarz criterion is meant to be more penalizing. | * It is remarquable that Akaike criterion and Hurvich and Tsai criterion are alike. AICc is therefore used for small sample size, but converges to AIC as n gets large. Since we will work with 20 points for each experiment, it seemed relevant to present both models. In addition, Schwarz criterion is meant to be more penalizing. | ||
* As an experiment, we wished to compare the two models presented below : | * As an experiment, we wished to compare the two models presented below : | ||
| - | System#1 : using the linear equations from our BOB approach : [[Image:syste_akaike_1.jpg]]<br> | + | '''System#1''' : using the linear equations from our BOB approach :<br> |
| - | System#2 : using classical Hill functions : [[Image:syste_akaike_2.jpg]]<br> | + | [[Image:syste_akaike_1.jpg]]<br> |
| + | '''System#2''' : using classical Hill functions :<br> | ||
| + | [[Image:syste_akaike_2.jpg]]<br> | ||
* We made a set of data out of a noised Hill function. In fact, our data set was made by using the same equations as System#2, but we introduced a normal noise for each point. Thus, System#1 is penalized because its RSS will be greater than that of System#2. Nevertheless, System#2 will be more penalized by its number of parameters. | * We made a set of data out of a noised Hill function. In fact, our data set was made by using the same equations as System#2, but we introduced a normal noise for each point. Thus, System#1 is penalized because its RSS will be greater than that of System#2. Nevertheless, System#2 will be more penalized by its number of parameters. | ||
Revision as of 12:42, 3 September 2008
 "
"