|
(Under Construction)
Model Comparison
- Using linear equations in a biological system might seem awkards. However, we wanted to check the relevance of this approach. We have been looking for a criterium that would penalize a system that had many parameters, but that would also penalize a system which quadratic error would be too important while fitting experimental values.
- Akaike and Schwarz criteria met our demands :
Akaike criterion :
Hurvich and Tsai criterion :
Schwarz criterion :
where n denotes the number of experimental values, k the number of parameters and RSS the residual sum of squares.
- It is remarquable that Akaike criterion and Hurvich and Tsai criterion are alike. AICc is therefore used for smal sample size, but converges to AIC as n gets large. Since we will work with 20 points for each experiment, it seemed relevant to present both models.
- As an experiment, we wished to compare two models presented below :
System #1 : using the linear equations :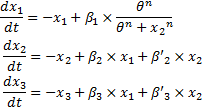 
System #2 : using classical Hill functions :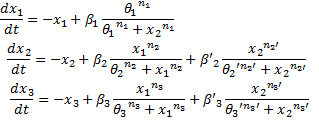 
We mostly used the definition of the criteria given in :
[http://www.liebertonline.com/doi/pdf/10.1089/rej.2006.9.324 K. Kikkawa.Statistical issue of regression analysis on development of an age predictive equation. Rejuvenation research, Volume 9, n°2, 2006.]
|
"
