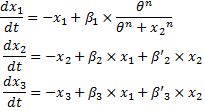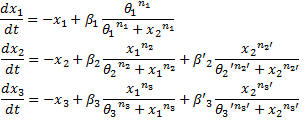|
(Under Construction)
Model Comparison
Short introduction to the criteria
- Using linear equations in a biological system might seem awkards. However, we wanted to check the relevance of this approach. We have been looking for a criterium that would penalize a system that had many parameters, but that would also penalize a system which quadratic error would be too important while fitting experimental values. The goal here is to decide whether, assuming that the experimental data looks like a model based on Hill functions, the linear part of the BOB model is obsolete or not.
- Akaike and Schwarz criteria taken from the information theory met our demands quite well :
Akaike criterion :
Hurvich and Tsai criterion :
Schwarz criterion :
where n denotes the number of experimental values, k the number of parameters and RSS the residual sum of squares.
The best fitting model is the one for which those criteria are minimized.
- It is remarquable that Akaike criterion and Hurvich and Tsai criterion are alike. AICc is therefore used for small sample size, but converges to AIC as n gets large. Since we will work with 20 points for each experiment, it seemed relevant to present both models. In addition, Schwarz criterion is meant to be more penalizing.
Experiment
- As an experiment, we wished to compare the two models presented below :
System#1 : using the linear equations from our BOB approach :
System#2 : using classical Hill functions :
- We made a set of data out of a noised Hill function. In fact, our data set was made by using the same equations as System#2, but we introduced a normal noise for each point. Thus, System#1 is penalized because its RSS will be greater than that of System#2. Nevertheless, System#2 will be more penalized by its number of parameters.
- With Matlab, we run a fitting simulation for each system, and we obtained the RSS. We then evaluated the different criteria for both models. The results are presented below.
| Comparison of the systems
|
| Criteria
| System#1
| System#2
|
| AIC
|
|
|
| AICc
|
|
|
| BIC
|
|
|
WHAT HAVE WE PROVED
We mostly used the definition of the criteria given in :
[http://www.liebertonline.com/doi/pdf/10.1089/rej.2006.9.324 K. Kikkawa.Statistical issue of regression analysis on development of an age predictive equation. Rejuvenation research, Volume 9, n°2, 2006.]
|
 "
"