Mutation Model

From 2008.igem.org

Part I Mutation Model

Hypothesis

  • The mutation efficiency from the initial gene to the target gene should remain a continuous curve along reproduction, or along time. Here we discrete the mutation rate to be linear function according to the replication time (), which in fact create several discontiguous point.
  • DNA lesion repair rate appears high enough in replication than other cell activities, so that the DNA lesion repair rate can be conformed to background mutations except in replication process.
  • The whole yeast is large enough to obey the statistics rules

Model Construction

  • Probability Model
    For each DNA sequence status, we take down a probability matrix for the coding sequence, which gives out each base appearance possibility on every site. The structure on each site is 5*1 matrix,(Pa,Pt,Pc,Pg,Pu), and ΣP=1. Therefore, the whole sequence status is recorded as 5*length matrix.E.g. For the Gal4 DNA, with a length of 2646, one status is a 5*2646 matrix.
  • Scanning Model
    The hotbox appearance rate on a specific site i is calculated as below.
Image:Peking hotbox search.jpg



W: a, t; R: a, g; H: a, c, g;
Hotbox appearrance rate PH=PW(i-2)PR(i-2)PC(i-2)PH(i-2), and here (i) refers to the site i.
  • Model on DNA lesion repair
    As reviewed by the paper, the U:G mismatch DNA lesion will be repaired in three pathways.Lacks of the knowledge on the preference of repair mechanism in yeast, we temporarily assume that mechanisms happen randomly.
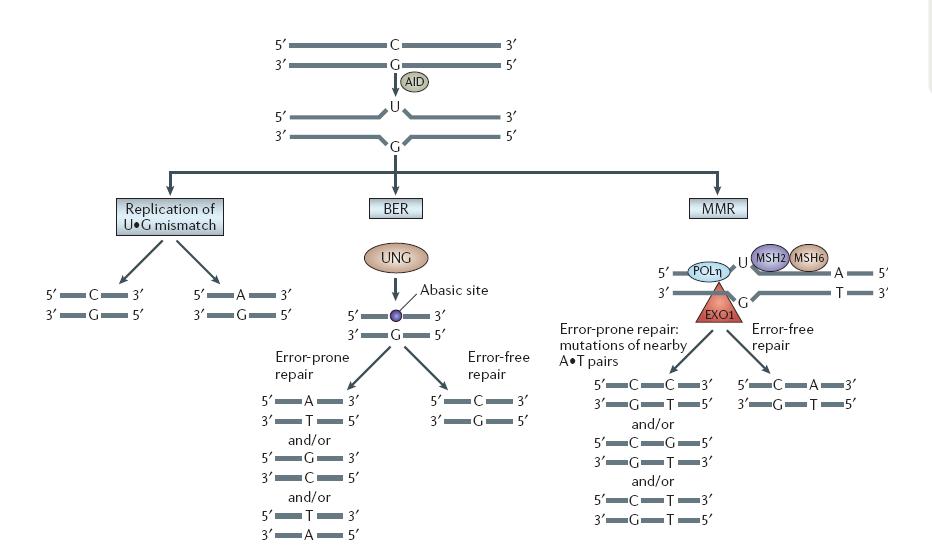
Image:Peking Repair.jpg
VH Odegard, DG Schatz. Targeting of somatic hypermutation. Nat Rev Immunol. 2006 Aug;6(8):573-83

  • Copy Status distribution along replication
    • Back ground mutations happen all the time in a fix rate.
    • Hotspot mutation happens in the transcription process on the coding DNA, while the lesion repair happen at the replication.
    • The figure below shows the whole process.Si is a sequence distribution matrix.
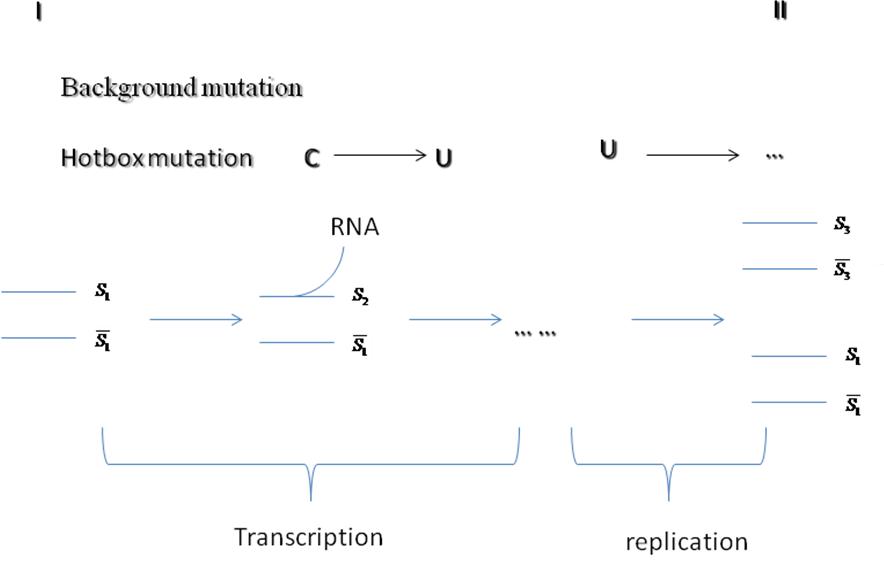
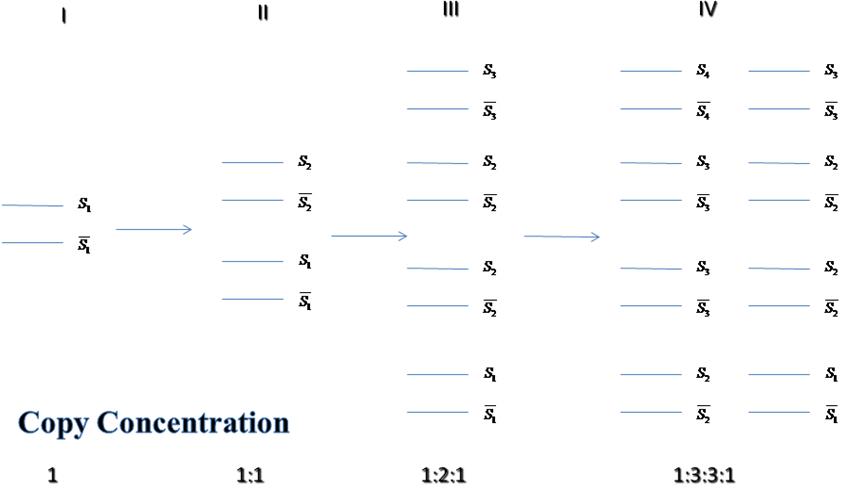
After n times replication, Copy concentration proportion from S1 to Sn+1 will be spread binomial expression of (1+1)n, which is Cn0:Cn1:n2:...:Cnn.
  • Result Calculation
    To find a probability from the initial gene to the target gene. Consider the DNA of Gal4 with a length of 2646, the target gene is a1a2a3a...a2545a2646.(Coding sequence)
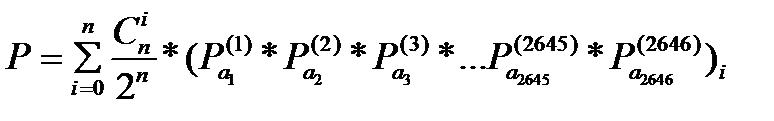
300px‎








Pa(j) is the probability of the base a on the site j, and (Pa1(1)*P**P*...P**P*)i means the calculation is based on the Si status matrix.
Previous Page
Retrieved from "http://2008.igem.org/Mutation_Model"