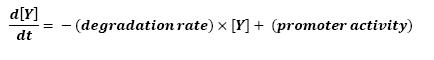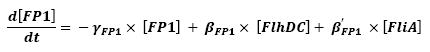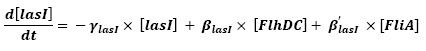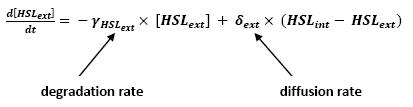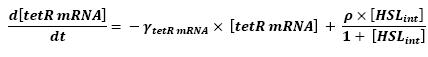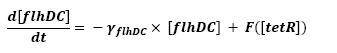Introduction
- Aims of the modeling part
- First approach proposed
- Hill functions
- first model + score function
- bibliography
- findparam
- experiments
- Second approach
- bibliography
- equations
- results
- experiments
- Continue the previous model
- Synchronyzation
- Estimation of the FIFO processes
- Stochastic modeling (Gilespie)
- Test of robustness
- Enhancing the system
- Better FIFO behaviour
- Other interactions to increase the robustness
Roadmap
If you want to have a look at our modeling notebook: Notebook
An Oscillatory Biological Model
Introduction
The goal here is to present the differential equations we used for our system modelization. At each step, we shall describe why we chose this precise model, its drawbacks and possible improvments, the parameters involved and enventually a biologically coherent value.
The key problem with a dynamic system consists in the fact that adding a new equation gives a more detailed idea of the overall process, but one looses precision by doing so since new parameters appear.
In that respect (in all cases but one) we chose not to model the mRNA steps, that is translation and transcription. We then assumed that we could act as if a protein would directly beget another one, without loosing too much precision.
This first approach only refers to a single cell. We shall examine later on what happens if we put more cells together.
Bibliography
Musch of our inspiration comes from four articles to which we shall refer in the next subsections :
[1] Shiraz Kalir, Uri Alon. Using quantitative blueprint to reprogram the dynamics of the flagella network. Cell, June 11, 2004, Vol.117, 713-720.
[2]Jordi Garcia-Ojalvo, Michael B. Elowitz, Steven H. Strogratz. Modeling a synthetic multicellular clock : repressilators coupled by quorum sensing. PNAS, July 27, 204, Vol. 101, no. 30.
[3]Nitzan Rosenfeld, Uri Alon. Response delays and the structure of transcription networks. JMB, 2003, 329, 645-654.
[4]Nitzan Rosenfeld, Michael B. Elowitz, Uri Alon. Negative autoregulation speeds the response times of transcription networks. JMB, 2003, 323, 785-793.
Equations
- Steps
- flhDC → fliA (1)
- flhDC → fliL → Fluorescent Protein 1 (FP1) (2)
- flhDC → flgA → Fluorescent Protein 2 (FP2) (3)
- flhDC → flhB → Fluorescent Protein 3 (FP3) (4)
- flhDC → flhB → lasI (5)
- fliA → fliL → Fluorescent Protein 1 (FP1) (6)
- fliA → flgA → Fluorescent Protein 2 (FP2) (7)
- fliA → flhB → Fluorescent Protein 3 (FP3) (8)
- fliA → flhB → lasI (9)
For all these equations, we found in [1] that in that precise case, the promoter activity the seven class 2 operons, among which fLiL, flgA, flhB, may be mathematically described in that way :
where [X] denotes the effective protein-level activity at time.
For each operon, Shiraz Kalir and Uri Alon came up with numerical values of β and β', available in [1].
Furthermore, the protein-level activity can be presented (for a more detailed presentation, see[4]) as
Thus :
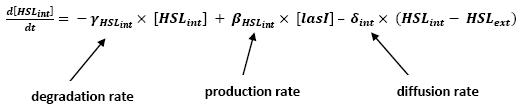
Even though we considered a single cell, we decided to model both HSL inside and outside the cell. In a first approach, we assumed that HSL could be modelized in the same fashion as AHL. The process was well detailed in [2].
- lasI → HSLext (10)
- lasI → HSLint (11)
Here is the only case where we coul not afford to skip the mRNA step. Then, (12) represents the binding and transcription steps ; (13) represents the translation step.
- HSLint → tetR mRNA (12)
- tetR mRNA → tet R (13)
hence :
Finally, the close the loop, we saw the necessity to use a little refinment. tetR influence over pTet, being the promoter of flhDC, is a repression. To express the non-instantaneous character of this interaction, we used a step function. To fully define this function, two parameters are needed, so as to describe the time when the step has to occur, and the initial value of this step. We are facing two solutions. The more accurate procedure would consist in getting those values from the wet-lab. However, we may also look for it in the literature. Anyhow, as presented in the conclusive part, there is a really wide range of parameters that enable the system to oscillate.
Parameters summary
Graph screenshots
First Mathematical Approach
Bibliography
In order to choose a proper modeling approach for our system, we have decided to list all the chemical reactions we will take into account. Afterwards, we will find the needed parameters reading articles or devising the required experiments.
An overview of the work that has to be done can be found here : Bibliography
Estimation of parameters
Estimation of the parameters
First Approach
First Approach
More precise Bio-Mathematical Description
Bio-Mathematical Description
|
 "
"