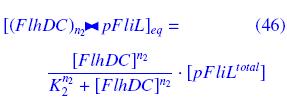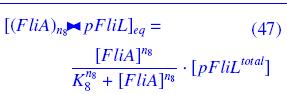Team:Paris/Modeling/FromMolReactToNLOde
From 2008.igem.org
(→Mathematical Interpretation and Simulation of the Molecular Reactions) |
(→Mathematical Interpretation and Simulation of the Molecular Reactions) |
||
| Line 29: | Line 29: | ||
{{Paris/Toggle|precisions|Team:Paris/Modeling/More_From2Ode_M}} | {{Paris/Toggle|precisions|Team:Paris/Modeling/More_From2Ode_M}} | ||
</div> | </div> | ||
| + | |||
| + | <br> | ||
Then, we apply these results to the <span style="color:#0000FF;">Molecular Reactions</span> of our system. That gives all the theoretical calculation of the complexations, and finally, with the <span style="color:#0000FF;">previous assumptions</span>, we get the <span style="color:#0000FF;">equations of the full system of ODEs</span>. | Then, we apply these results to the <span style="color:#0000FF;">Molecular Reactions</span> of our system. That gives all the theoretical calculation of the complexations, and finally, with the <span style="color:#0000FF;">previous assumptions</span>, we get the <span style="color:#0000FF;">equations of the full system of ODEs</span>. | ||
Revision as of 13:54, 27 October 2008
|
From Molecular Reactions to Non-Linear ODEs
[Back to "Workflow on an Example"] Idea and AssumptionsWe will here propose a Mathematical Modeling of the elementary molecular reactions. The idea of the Characterization Approach is that this modelization must both accounts for every small steps of the system and allow the experimental characterizations. ↓ precisions ↑
Therefore, the following equations do not describe properly what really happens in the cells. For exemple, we know that the transcription factor FlhD-FlhC is actually an hexamere FlhD4C2. But, as we will surely not get access to the dissociation constant of the hexamerisation, we just treat it as an abstract inducer protein "FlhDC", with an order (n) in its complexation caracterization probably around 2*4 = 8 (but perhaps completly different ! ; the estimation of the error by the parameter finder program would tell us if it stays consistent). ↓ all assumptions ↑
Mathematical Interpretation and Simulation of the Molecular ReactionsFirst, we consider the complexation phenomenon. We show, under the quasi steady-state hypothesis, how it leads to Non-Linear interactions like "Hill functions". ↓ precisions ↑
Then, we apply these results to the Molecular Reactions of our system. That gives all the theoretical calculation of the complexations, and finally, with the previous assumptions, we get the equations of the full system of ODEs.
for complete .pdf with all reactions and references : [list of reactions/equations]
|
 "
"