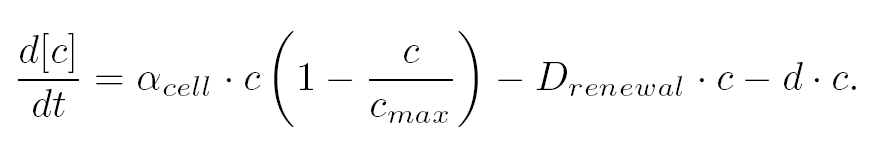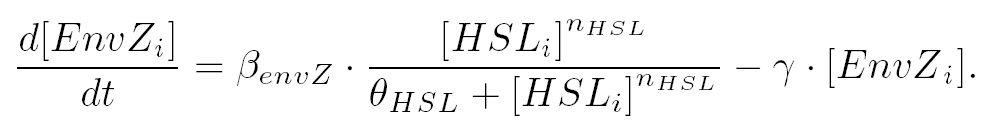|
Model Construction
Motivation
We are interested to understand the factors that account for an oscillating behaviour at population level. We build two models to study systems that are equipated with quorum sensing capabilities but that relay on different designs principles. The proposed models are:
- In the one model, we use a modular design. We consider that the core system is one of the modules of the system. In adittion, the other module is an two gene oscillator system presented in (Garcia-Ojalvo) that accounts for quorum sensing.
- In the other model, we rewire the architecture of the core system to have the desired functionality of the system in a single circuit.
Both the modular and the all-in-one models describe events that happend not only at the cellular level (as in the core system) but also at the population level due to interactions needed bettwen a cell and its environment during quorum sensing.
In the following sections, we first describe the population modeling (the common part amoung our two proposed models) to then focus our attention to the characteristics that are exclusive to each of the modeling alternatives.
Population Modeling
- A chemostat is generally used to keep bacteria volume constant in the medium. The constant conditions provided by the chemostat help us to control bacteria growth rate.
- We assume a logistic model to determine bacteria growth in the chemostat, in agreement with standar procedures (reference). This hypothesis implies that bacteria growth rate has to be proportional to the existing bacteria population size and to the amount of available resources in the medium.
- As discussed previously, we choose to use quorum sensing as a way to improve the oscillating behaviour of our core system and, at the same time, as a way to archeive population synchronization. When a cultive of bacteria is synchronized, it means that every single cell express in average the same genes in unison. As a result, a maximum level of fluorescense is obtained.
Kinetics
| Common Dynamics
|
| The variation of cells' concentration in the chemostat over time can be expressed in terms of a production (positive) term and degradation (negative) terms:
|
| Modular system
| All-in-one system
|
| Modular system
| All-in-one system
|
| Synchronized oscillations should be given by All-in-one system.
|
- The variation of cells' concentration in the chemostat over time can be expressed in terms of a production (positive) term and degradation (negative) terms:
|
|
| For the production term, we use a logistic equation to model cell growth, according to standard assumptions [Garcia-Ojalvo]. The behaiviour obtained is the following one: at low population density, the concentration of cells in the chemostat (c) increase exponentialy with a growth rate αcell and at high population density, the population reaches a maximum concentration, cmax.
|
| For the degradation term, we consider that c decrease proportionaly to both a dilution phenomena cause by the renewal of the medium in the chemostat (Drenewal) and cell death (d).
|
- To model the quorum sensing dynamics, we consider:
| Intracellularly, the HSL dynamics follows:
|
|
|
| intercellularly, the HSL concentration is given by:
|
|
|
| that is equivalent to:
|
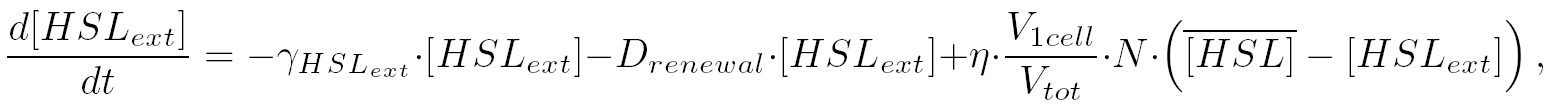
|
where 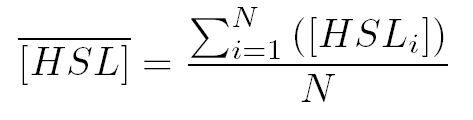 and and 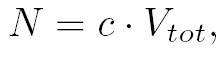
|
| and the activation of envZ depends of the concentration of HSL according to:
|
|
|
Parameters Search
manly from literature but also from S0 analysis.
| Parameters
|
|
|
| Chemostat
| Parameter
| Meaning
| Original Value
| Normalized Value
| Unit
| Source
|
| figure / equations of Chemostat
| αcell
| Growth rate
| 0.0198
| 1
| min-1
| wet-lab
|
| cmax
| Carrying capacity for cell growth
| 0.1
| 0.1
| µm3
| [3]
|
| Drenewal
| Dilution rate
| 0.00198
| 0.1
| min-1
| wet-lab ([3])
|
| d
| Death rate
| 0.0099
| 0.5
| min-1
| wet-lab
|
|
|
| Quorum Sensing
| Parameter
| Meaning
| Original Value
| Normalized Value
| Unit
| Source
|
| figure / equations of Quorum Sensing
| γHSL
| Degradation rate
| 0.0053
| 0.2690
| min-1
| wet-lab
|
γHSLext
| Degradation rate
| 0.0106
| 0.5380
| min-1
| [6]
|
| βHSL
| Production rate
| 0.3168
| 16
| min-1
| ∅
|
| η
| Diffusion rate
| 10
| 505
| min-1
| [2]
|
| nHSL
| Hill coefficient
|
| 4
|
| [3]
|
| θHSL
| Hill characteristic concentration for the second operator
|
| 0.5
| c.u
| [3]
|
|
 "
"