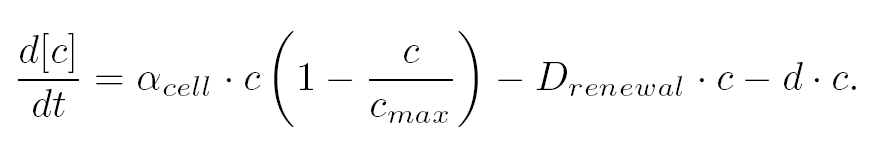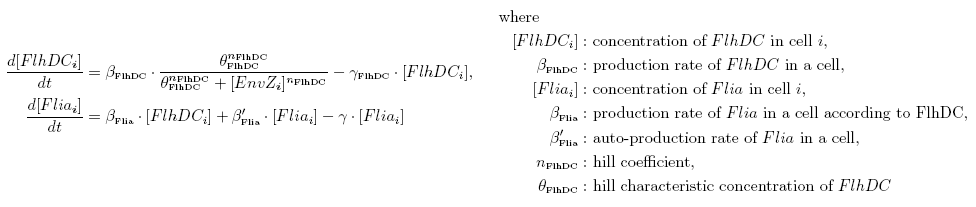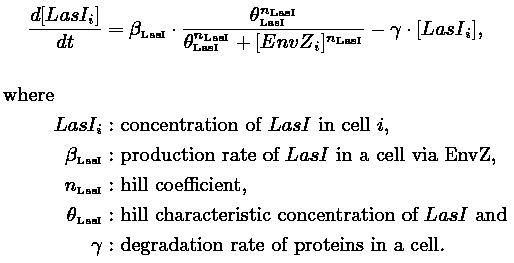Team:Paris/Analysis/Construction2
From 2008.igem.org
(→Description) |
(→Motivation) |
||
| Line 2: | Line 2: | ||
{{Paris/Header|Model Construction}} | {{Paris/Header|Model Construction}} | ||
| - | == | + | == Construction == |
| - | We are interested to understand the factors that account for an oscillating behaviour at population level. We build two models to study systems that are equipated with quorum sensing capabilities but that relay on different designs principles. The proposed models are: | + | We are interested to understand the factors that account for an oscillating behaviour at population level. We build two models to study systems that are equipated with quorum sensing capabilities but that relay on different designs principles. |
| + | |||
| + | == Modeling Alternatives == | ||
| + | |||
| + | The proposed models are: | ||
*In the one model, we use a modular design. We consider that the core system is one of the modules of the system. In adittion, the other module is an two gene oscillator system presented in [[Team:Paris/Modeling/BOB#Bibliography|[Garcia-Ojalvo]]] that accounts for quorum sensing. We call this alternative the 'bimodular system'. | *In the one model, we use a modular design. We consider that the core system is one of the modules of the system. In adittion, the other module is an two gene oscillator system presented in [[Team:Paris/Modeling/BOB#Bibliography|[Garcia-Ojalvo]]] that accounts for quorum sensing. We call this alternative the 'bimodular system'. | ||
Revision as of 11:19, 28 October 2008
|
Model Construction
ConstructionWe are interested to understand the factors that account for an oscillating behaviour at population level. We build two models to study systems that are equipated with quorum sensing capabilities but that relay on different designs principles. Modeling AlternativesThe proposed models are:
Both the bimodular and unimodular models describe events that happend not only at the cellular level (as in the core system) but also at the population level due to interactions needed bettwen a cell and its environment during quorum sensing. In the following sections, we first describe the population modeling (the common part amoung our two proposed models) to then focus our attention to the characteristics that are exclusive to each of the modeling alternatives. Description
Parameters SearchThe following table sumarize our findings. The parameters' values that are used during the simulations. Most them are found in literature others are obtained from further analysis.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 "
"