Introduction
- Aims of the modeling part
- First approach proposed
- Hill functions
- first model + score function
- bibliography
- findparam
- experiments
- Second approach
- bibliography
- equations
- results
- experiments
- Continue the previous model
- Synchronyzation
- Estimation of the FIFO processes
- Stochastic modeling (Gilespie)
- Test of robustness
- Enhancing the system
- Better FIFO behaviour
- Other interactions to increase the robustness
Roadmap
If you want to have a look at our modeling notebook: Notebook
An Oscillatory Biological Model
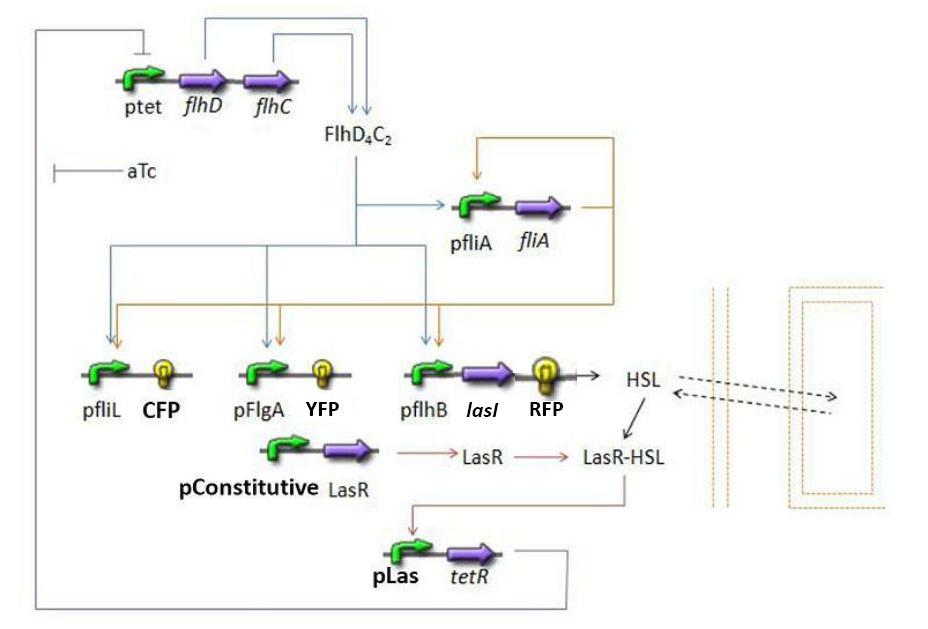 Overall Model Overall Model Introduction
The goal here is to present the differential equations we used in the system modelization. At each step, we shall describe why we chose this precise model, its drawbacks and possible improvments, the parameters involved and enventually a biologically coherent value.
The key problem with a dynamic system consists in the fact that adding a new equation gives a more detailed idea of the overall process, but one looses precision by doing so since new parameters appear.
In that respect (in all cases but one) we chose not to model the mRNA steps, that is translation and transcription. We then assumed that we could act as if a protein would directly act upon the follower, without loosing too much precision.
This first approach refers to a set of two cells. We shall examine later on what happens if we put more cells together.
Bibliography
Much of our inspiration comes from four articles to which we shall refer in the next subsections :
- [1] Shiraz Kalir, Uri Alon. Using quantitative blueprint to reprogram the dynamics of the flagella network. Cell, June 11, 2004, Vol.117, 713-720.
- [2]Jordi Garcia-Ojalvo, Michael B. Elowitz, Steven H. Strogratz. Modeling a synthetic multicellular clock : repressilators coupled by quorum sensing. PNAS, July 27, 204, Vol. 101, no. 30.
- [3]Nitzan Rosenfeld, Uri Alon. Response delays and the structure of transcription networks. JMB, 2003, 329, 645-654.
- [4]Nitzan Rosenfeld, Michael B. Elowitz, Uri Alon. Negative autoregulation speeds the response times of transcription networks. JMB, 2003, 323, 785-793.
- [5]S.Kalir, J. McClure, K. Pabbaraju, C. Southward, M. Ronen, S. Leibler, M. G. Surette, U. Alon. Ordering genes in a flagella pathway by analysis of expression kinetics from living bacteria. Science, June 2001, Vol 292.
Equations
- Steps
- flhDC → fliA (1)
- flhDC → fliL → Fluorescent Protein 1 (FP1) (2)
- flhDC → flgA → Fluorescent Protein 2 (FP2) (3)
- flhDC → flhB → Fluorescent Protein 3 (FP3) (4)
- flhDC → flhB → lasI (5)
- fliA → fliL → Fluorescent Protein 1 (FP1) (6)
- fliA → flgA → Fluorescent Protein 2 (FP2) (7)
- fliA → flhB → Fluorescent Protein 3 (FP3) (8)
- fliA → flhB → lasI (9)
The transcription hierarchy of the flagella genes have been studied in [1]. It resulted that the promoter activity of the seven class 2 operons, among which fLiL, flgA, flhB, may be mathematically described in that way :
where [X] denotes the effective protein-level activity.
For each operon, Shiraz Kalir and Uri Alon came up with numerical values of β and β', available in [1].
Furthermore, the protein-level activity can be presented (for a more detailed presentation, see[4]) as
Thus :
- Discution and Asumptions
- As presented in the first equation below, there is a retroaction from fliA over fliA. In a first approach, we decided not to take into account this interaction, that is setting β'FliA to zero. In a second approach, we will consider this retroaction, and find a way to describe it mathematically.
- Another step consists in choosing the proper units, so as to have a homogenous set of parameters. In fact we need temporal parameters, but those given in the article are measured with the derivative of GFP over OD. Since we will work with a constant population density, we should only need to add a multiplicative factor, that we shall determine thanks to biological processes.
- Steps
- lasI → HSLext (10)
- lasI → HSLint (11)
- Discution and Asumptions
- In a first approach, we have assumed that HSL could be modelized in the same fashion as AHL. The process was well detailed in [2] and we adapted their model to our present situation. Furthermore, a biologically coherent set of parameters is also given in this article. We decided then to use them as well for our simulation.
- Steps
- HSLint → tetR mRNA (12)
- tetR mRNA → tet R (13)
- Discution and Asumptions
- Here is the only case where we have not yet found out how we could manage to skip the mRNA step. However, this is acceptable since every parameter should be available. Then, (12) represents the binding and transcription steps ; (13) represents the translation step.
- The effect of HSL as well as the link between the mRNA activity and protein activity is well studied in [2]. We were the able to adapt the introduced situation to our system.
- The ρ parameter corresponds to maximal contribution to tetR transcription in presence of saturating amounts of HSL. Yet, to begin with, we have used the parameter given in the text. We shall then find a more accurate parameter corresponding to our system. The HSL activation is hereby chosen to follow Michalelis Menten kinetics since we assumed that there would be no cooperativity.
- Finally, we assumed that lasR would exist permanently in the medium in sufficient amounts, so that we needn't take it into account mathematically speaking.
- Discution and Asumptions
- To determine this part of the model, we used [4] where the influence of tetR is described.
- Finally, to close the loop, we saw the necessity to use a little refinment. the influence of tetR over pTet (pTet being the promoter of flhDC) is a repression. To express the fact that a certain concentration is needed for the expression of flhDC, we used a step function. This choice was influenced by [3]. To fully define this function, two parameters are needed, so as to describe the threshold when the step has to occur, and the initial value of this step. We are facing two solutions. The more accurate procedure would consist in getting those values from the wet-lab. However, we may also look it up in the literature. Anyhow, as presented in the conclusive part, there is a really wide range of parameters that enable the system to oscillate.
- The key problem was that those two parameters were to be determined by the overall evolution of tetR, and the program cannot wait for tetR to be entirely determined to evaluate flhDC, since we have a loop. We then decided that these parameters could be obtanied by lab experiments.
Parameters summary
- Awaiting for experimental values, since it seemed coherent by reading articles, we have chosen to set every degradation rate to 1.
| Parameter Table
|
| Parameter
| Parameter in code (cell i)
| Meaning
| Value
| Unit
| Source
| Accuracy
| Comments
|
| γFliA
| g[1 + 8 x (i-1)]
| Degradation rate
| 1
|
| [1]
|
|
|
| βFliA
| B(1,i)
| FlhDC activation coefficient
| 50
|
| [1]
|
|
|
| β'FliA
| b(1,i)
| FliA activation coefficient
| 0
|
| [1]
|
|
|
| γFP1
| g[2 + 8 x (i-1)]
| Degradation rate
| 1
|
| [1]
|
|
|
| βFP1
| B(2,i)
| FlhDC activation coefficient
| 1200
|
| [1]
|
|
|
| β'FP1
| b(2,i)
| FliA activation coefficient
| 250
|
| [1]
|
|
|
| γFP2
| g[3 + 8 x (i-1)]
| Degradation rate
| 1
|
| [1]
|
|
|
| βFP2
| B(3,i)
| FlhDC activation coefficient
| 150
|
| [1]
|
|
|
| β'FP2
| b(3,i)
| FliA activation coefficient
| 300
|
| [1]
|
|
|
| γFP3
| g[4 + 8 x (i-1)]
| Degradation rate
| 1
|
| [1]
|
|
|
| βFP3
| B(4,i)
| FlhDC activation coefficient
| 100
|
| [1]
|
|
|
| β'FP3
| b(4,i)
| FliA activation coefficient
| 350
|
| [1]
|
|
|
| γlasI
| g[4 + 8 x (i-1)]
| Degradation rate
| 1
|
| [1]
|
|
|
| βlasI
| B(4,i)
| FlhDC activation coefficient
| 100
|
| [1]
|
|
|
| β'lasI
| b(4,i)
| FliA activation coefficient
| 350
|
| [1]
|
|
|
γHSLint
| g[5 + 8 x (i-1)]
| Degradation rate
| 1
|
| [1]
|
|
|
βHSLint
| B(5,i)
| Production rate
| 0,01
|
| [2]
|
|
|
| δint
| D(1,i)
| Diffusion rate in the cell
| 2
|
| [2]
|
|
|
γHSLext
| g[6 + 8 x (i-1)]
| Degradation rate
| 1
|
| [1]
|
|
|
| δext
| D(2,i)
| Diffusion rate out off the cell
| 2
|
| [2]
|
|
|
| γtetR mRNA
| g[6 + 8 x (i-1)]
| Degradation rate
| 1
|
| [1]
|
|
|
| ρ
| R(i)
| Maximal contribution to tetR in the presence of saturating amounts of HSL
| 20
|
| [2]
|
|
|
| θ
| 0(i)
| Ratio between mRNA and protein lifetimes
| 1
|
| [2]
|
|
|
| γflhDC
| g[8 + 8 x (i-1)]
| Degradation rate
| 1
|
| [1]
|
|
|
| τ
| T(i)
| Threshold for tetR repression
| (20000)
|
| lab
|
|
|
| ∆
| Pa(i)
| Promoter activity without the repressor
| (100)
|
| lab
|
|
|
Graph screenshots
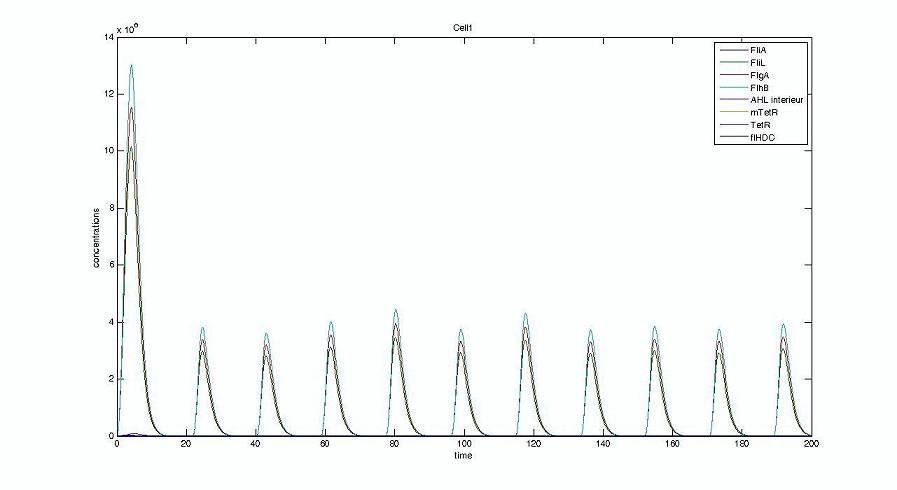 Cell1 in a 2 cells model : oscillations and a glimpse of FIFO Cell1 in a 2 cells model : oscillations and a glimpse of FIFO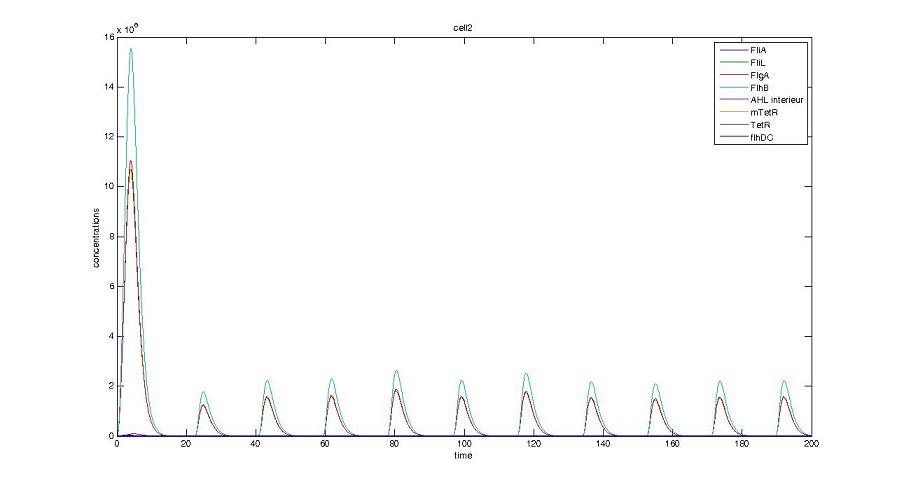 Cell2 (noise added to set the parameters) in a 2 cells model : oscillations and a glimpse of FIFO Cell2 (noise added to set the parameters) in a 2 cells model : oscillations and a glimpse of FIFO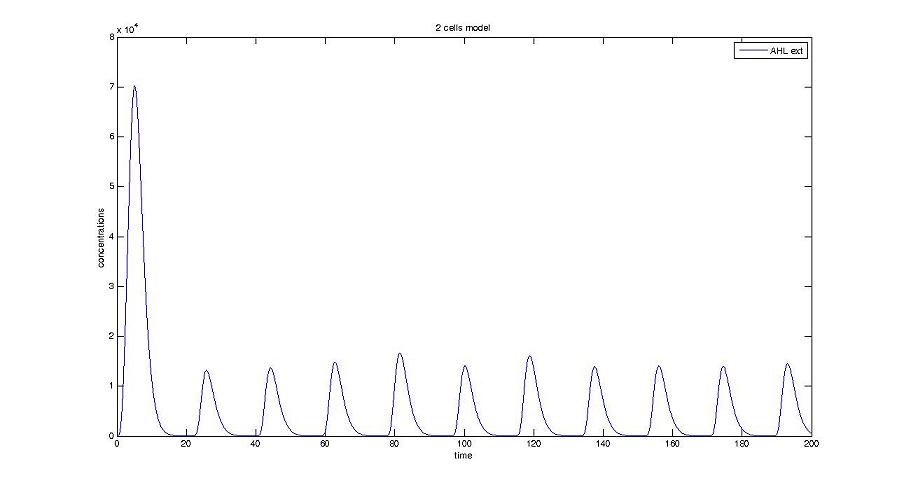 HSL ext in a 2 cells model : oscillations HSL ext in a 2 cells model : oscillations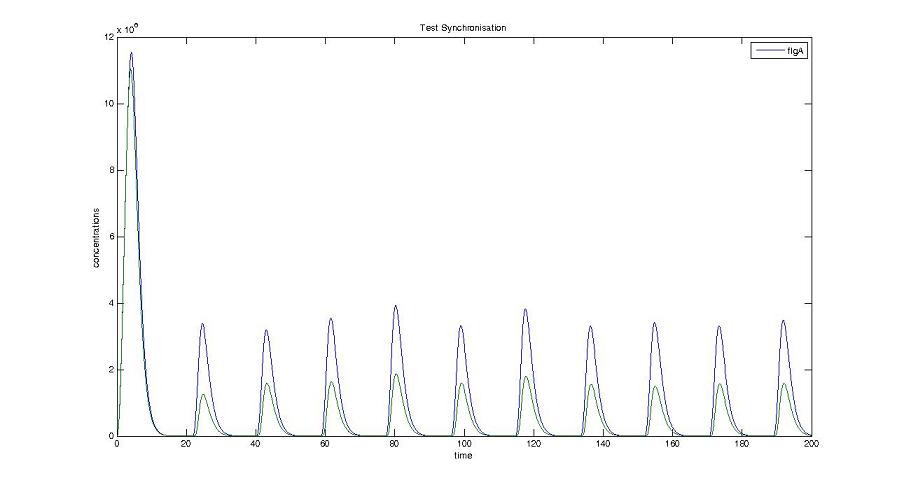 Synchronisation : flgA in both cells Synchronisation : flgA in both cells Synchronisation : fliL in both cells Synchronisation : fliL in both cells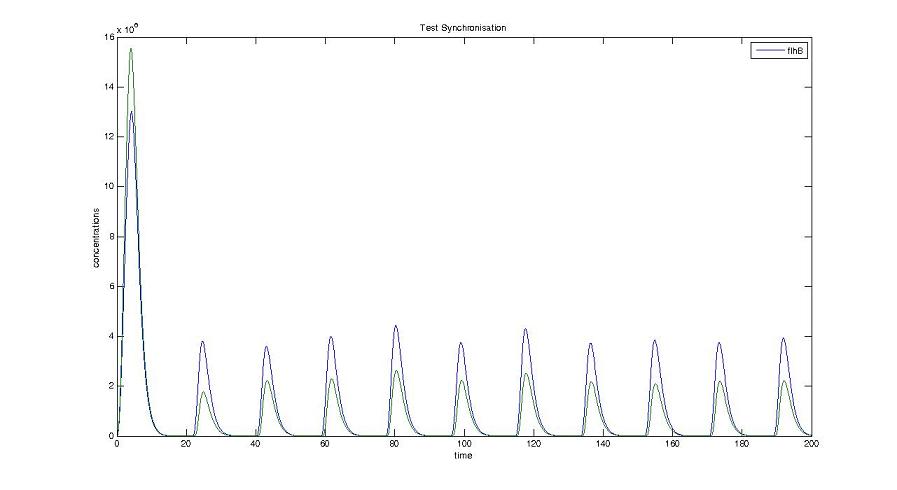 Synchronisation : flhB in both cells Synchronisation : flhB in both cells Corresponding codes
- To change the parameters, you have to use this file, and refer to the previous array : Model
- To launch the numerical simulation and plot the curves : Plot the curves
- To compute the numerical simulations (does not provide any visual output, but necessary for the previous script) : Numerical simulations
Discussion
- In [1], we had trouble deciding whether the parameters we used were coherent or not, and we spent some time checking abouts units. Thus, we had to decide how we shall set our time unit.
- We found a seemingly acceptable answer using elements from [1] and [5].
- If you compare these results with our program codes, you might see that we did not take the α factor into account. However, we understant this factor so as to make our time scale. In fact, we are given the time taken by a population to double its size. Since, we have a classical
| Equations
| Tdouble-equations = ln2 / α
| Reality
| Tdouble ~ 20 min
|
- This enabled us to set a real x-axis unit, because we had decided at first to set α to 1. We then tried to compared our results to those found in [5].
Concerning the parameters taken from [2], it has to be noticed that output units are arbitrary. Nonetheless, as the degradation rate is also 1, as in [1], one can infer that the transformation to obtain the 'real' time and Fluorescence units are the same in [2] than in [1].
Thanks to that assumptions, we are finally able to end up with a quantitative description of the biological system, instead of just a qualitative one.
First Mathematical Approach
Introduction
As a first approach, we had decided to take into account the binding to the promoters steps. Moreover, the transcription rates were expected to be Hill functions. Obvisouly, this modeling requires a huge number of parameters. To obtain them, we had planed to devise specific experiments (described below).
Nonetheless, after reading some more articles, we have decided to change several asumptions of the modeling choice. Therefore, we have devised a perhaps more biologically relevant framework (see above).
This part describes in detail the first approach and the codes that have been produced.
First Approach
As a first approximation, we have proposed a set of 5 ordinary differential equations, without taking into account the transcription step. Besides, we have had not introduced yet a synchronizaton module. Therefore, the repression of FlhDC is directly modeled by the presence of the 'Z3' gene (that is the last that is turned on).
In this framework, we have found parameters that have provided oscillations as well as a function that automatically detects whether the output of the ode system is oscillating. This has allowed to screen a little the parameters used, in order to evaluate the robustness of the system.
The methods employed are described there : First Approach.
More precise Bio-Mathematical Description
After trying to obtain oscillations from a simple model, we have tried to described more precisely the studied system. Therefore, we have obtained the following formalism : Bio-Mathematical Description.
Bibliography
In order to choose a proper modeling approach for our system, we have decided to list all the chemical reactions we will take into account. Afterwards, we will find the needed parameters reading articles or devising the required experiments.
An overview of the work that has to be done can be found here : Parameters we have to use.
Estimation of parameters
Then, we will need many parameters to fully desribe the system according to the asumptions of the previous section. A natural way to have access to their value, after searching in the litterature, is to devise specific experiments. As a consequence of the characterization of the promoters activity, some Hill functions could be obtained.
Thus, we have described the experimental approach required : Estimation of the parameters.
Nonetheless, as mentioned above, we have changed the way to model the biological reactions. As a result have stopped investigating in this way to focus on the An Oscillatory Biological Model.
|