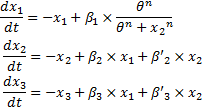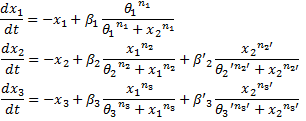Team:Paris/Network analysis and design/Core system/Model construction/Akaike
From 2008.igem.org
- When building a model, it is of the utmost importance to present a justification of the choice made along the transposition process from biological reality to mathematical representation. The aim of this section is to introduce a mathematical justification of the choice we made since it seems remote from biological reality. The criterion presented below are to help choosing the most relevant model given the experimental constraints.
Short introduction to the criteria
- Using linear equations in a biological system might seem awkward. However, we did prove the relevance of this approach. We have been looking for a criterion that would penalize a system that had many parameters, but that would also penalize a system which quadratic error would be too important while fitting experimental values. The goal here is to decide whether, assuming that the experimental data looks like a model based on Hill functions, the linear part of the model is obsolete or not.
- Several criteria taken from the information theory met our demands quite well :
where n denotes the number of experimental values, k the number of parameters and RSS the residual sum of squares. The best fitting model is the one for which those criteria are minimized.
- It is remarkable that Akaike criterion and Hurvich and Tsai criterion are alike. AICc is therefore used for small sample size, but converges to AIC as n gets large. Since we will work with 20 points for each experiment, it seemed relevant to present both criteria. In addition, Schwarz criterion is meant to be more penalizing.
Experiment
- As an experiment, we compared the two models presented below :
System#1 : using the linear equations found in bibliography :
System#2 : using classical Hill functions :
- We made a set of data out of a noised Hill function. In fact, our data set was made by using the same equations as System#2, but we introduced a normal noise for each point. Thus, System#1 is penalized because its RSS will be greater than that of System#2. Nevertheless, System#2 will be more penalized by its number of parameters.
- With Matlab, we run a fitting simulation for each system, and we obtained the RSS. We then evaluated the different criteria for both models. We chose to act as if the length of our experimental data set was 20 (which is what we would have gotten in reality). The results are presented below.
| Comparison of the systems for n=20 | ||
|---|---|---|
| Criteria | System#1 | System#2 |
| AIC | 26.7654 | 32.0035 |
| AICc | 38.7654 | 168.0035 |
| BIC | 22.9435 | 24.3596 |
| Comparison of the systems for n=100 | ||
|---|---|---|
| Criteria | System#1 | System#2 |
| AIC | 169.5495 | 32.1150 |
| AICc | 171.1147 | 38.5912 |
| BIC | 172.0100 | 37.0360 |
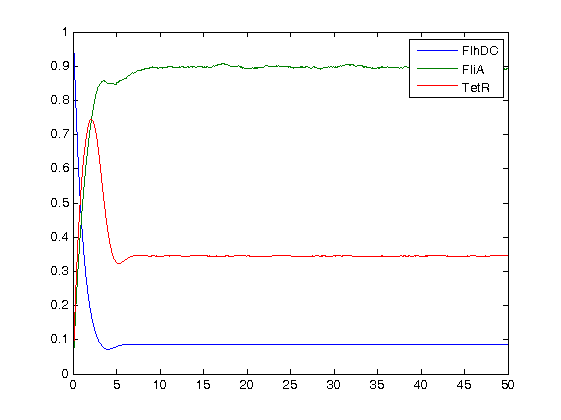
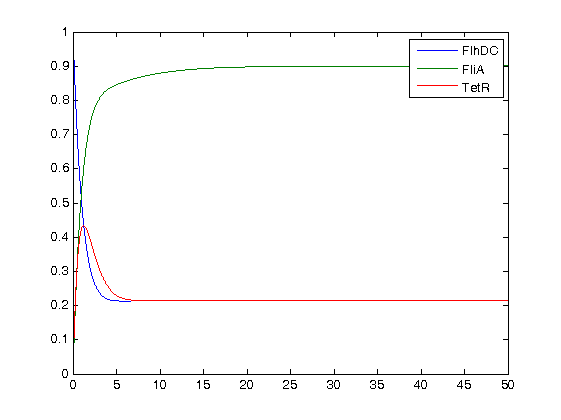
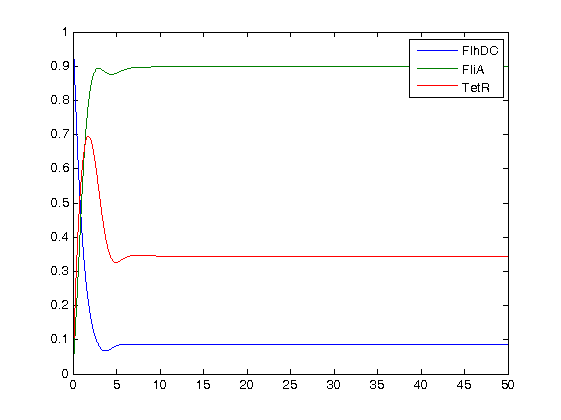
- Finally, we ran the simulation plots obtained for the parameters that best fitted. Here are the results proving that no numerical errors were to be seen :
Then, we see that the model that uses linear equations does not fit that well, but under certain conditions it is not so bad. Indeed, if the data set is short, this kind model is a relevant model since it eases the understanding of the dynamics.
- Consequently, what have we proved? These results show that:
- We may see that, as predicted, System#2 is not penalized anymore for greater values of n, although System#1 is. Consequently, we may adapt our system knowing the length of the data set we are going to obtain experimentally.
- However, since for a larger set of data System#2 minimizes the criteria, these criteria cannot decide whether a model is "better" than another one, since those criteria are arbitrary. Yet, they may help us find a better compromise between simplification and accuracy.
- Consequently, these criteria corroborate our choice of a linear model.
A fundamental tool?
Why can we introduce this seemingly awkward criteria as being a fundamental tool? This precise criteria enables the mathematician to adapt its model. In fact, in that respect, conducting this analysis over his model gives tangible arguments to the mathematician to use such and such model. Indeed, in our precise case, if we have about 20 experimental points to fit, the linear approach is sufficient. However, if we get 50 points, it becomes inadequate compared to a model with Hill functions. We believe that this kind of criteria is an essential tool, that might help the model maker to comprehend and control the assumptions he made while creating his model.
- We mostly used the definition of the criteria given in :
[http://www.liebertonline.com/doi/pdf/10.1089/rej.2006.9.324 K. Kikkawa.Statistical issue of regression analysis on development of an age predictive equation. Rejuvenation research, Volume 9, n°2, 2006.]
 "
"