Team:Paris/Modeling/Oscillations

From 2008.igem.org

(Difference between revisions)
(→Resulting Equations)
(→Biochemical Assumptions)
Line 20: Line 20:
In the same way, a '''repressible promoter''' has got a '''basal expression''', and its expression is proportionnal to the number of '''free promoters'''.
In the same way, a '''repressible promoter''' has got a '''basal expression''', and its expression is proportionnal to the number of '''free promoters'''.
-
Moreover, even if generally the amount of a ''transcription factor'' is far superior than the amount of the corresponding promoter, because our ''complexation equation'' (see [[Team:Paris/Modeling/Programs]]), we have to take into acount that if a ''transcription factor'' binds to several promoters, those two complexations are in competition.  
+
Moreover, even if generally the amount of a ''transcription factor'' is far superior than the amount of the corresponding promoter, because our ''complexation equation'' (see [[Team:Paris/Modeling/Programs]]), we have to take into acount that if several ''transcription factors'' bind to a given promoter, those several complexations are in competition.  
-
In this way, we assume that all the steady-states of the complexations are reached '''at the same time''', without taking into acount a possible kinetically predominant reaction : the singles complexation equations are put together in a consistent system.
+
To treat this phenomenon, we must know if a reaction is ''predominant'', or if all the steady-states are reached "at the same time". We made the following hypothesis :
-
Endly, we suppose that the contribution of the two inducers FliA and FlhDC on ''PflhB'' are synthetised by a ''' ''SUM'' logical gate'''.
+
* The contribution of the two inducers FliA and FlhDC on ''pFlhB'' are synthetised by a ''' ''SUM'' logical gate''' : that corresponds to the biological hypothesis that the promoter has got two specific sites of binding, one for each ''TF''.
 +
 
 +
*
==Resulting Equations==
==Resulting Equations==

Revision as of 06:34, 18 September 2008

Contents

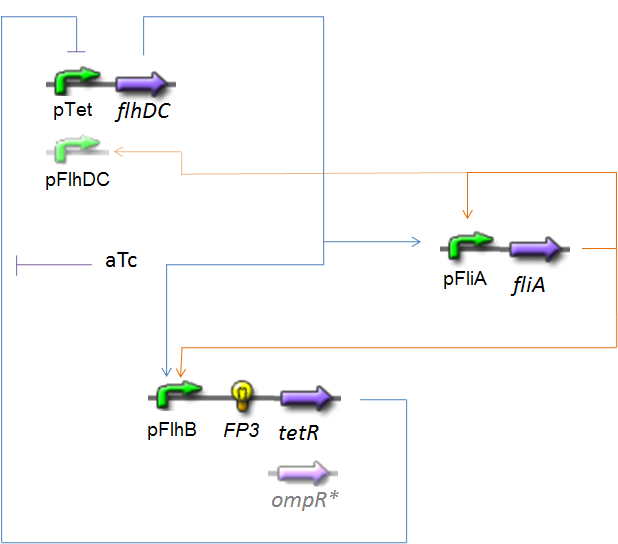
Oscillations

The Circuit

We just keep here the following circuit, constituing the Oscillations. The gene FP3 codes for the third reporter protein we will use in our final system.

We have two alternatives for the promoter before flhDC : pTet or pFlhDC. These two alternatives are both studied in what follows.


Model Oscillat.png

Biochemical Assumptions

We do not take into acount the phenomenon of translation : we consider the transduction as leading directly to the production of the protein (see however considerations on RBS).

We assume that the expression rate of an inducible promoter is proportionnal to the number of created complexes promoter-inducer.

In the same way, a repressible promoter has got a basal expression, and its expression is proportionnal to the number of free promoters.

Moreover, even if generally the amount of a transcription factor is far superior than the amount of the corresponding promoter, because our complexation equation (see Team:Paris/Modeling/Programs), we have to take into acount that if several transcription factors bind to a given promoter, those several complexations are in competition. To treat this phenomenon, we must know if a reaction is predominant, or if all the steady-states are reached "at the same time". We made the following hypothesis :

  • The contribution of the two inducers FliA and FlhDC on pFlhB are synthetised by a SUM logical gate : that corresponds to the biological hypothesis that the promoter has got two specific sites of binding, one for each TF.

Resulting Equations

First, we introduce here what we assume to be in our model the involved chemical reactions. They are written in black, regards to the equations that concerns both of the alternatives.

Then, the red and green equations are those implemented in our simulation programs.

The blue ones correspond to the reactions of complexation, and the red ones just below are the complexations functions that are their consequences if their stady-state are immediatly reached (see Biochemical Assumptions).

The green ones correspond to the reaction of production of proteins.


Retrieved from "http://2008.igem.org/Team:Paris/Modeling/Oscillations"