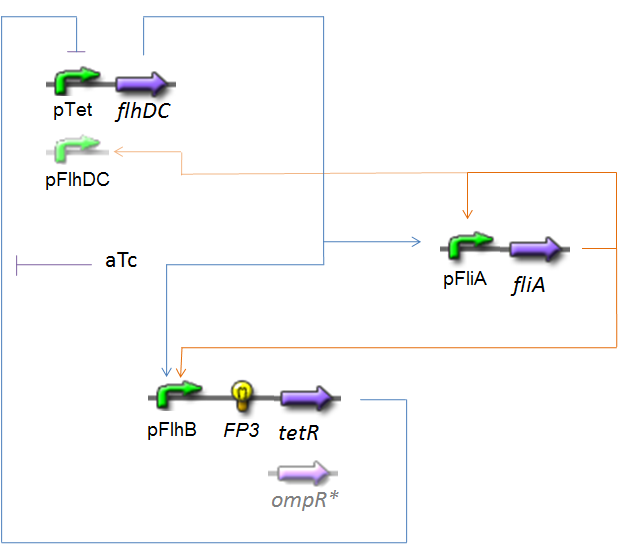
Oscillations

The Circuit

We just keep here the following circuit, constituing the Oscillations. The gene FP3 codes for the third reporter protein we will use in our final system.

We have two alternatives for the promoter before flhDC : pTet or pFlhDC. These two alternatives are both studied in what follows.

Biochemical Assumptions

We do not take into acount the phenomenon of translation : we consider the transduction as leading directly to the production of the protein (see however considerations on RBS).

We assume that the expression rate of an inducible promoter is proportionnal to the number of created complexes promoter-inducer.

In the same way, a repressible promoter has got a basal expression, and its expression is proportionnal to the number of free promoters.

Generally, the amount of a transcription factor is far superior than the amount of the corresponding promoter, even if it binds to several promoters (see the complexation equation ). But, in contrario, we have to take into acount that if several transcription factors bind to a given promoter, those several complexations are in competition. To treat this phenomenon, we must know if a reaction is predominant, or if all the steady-states are reached "at the same time". We made the following hypothesis :

• The contribution of the two inducers FliA and FlhDC on pFlhB are synthetised by a SUM logical gate : that corresponds to the biological hypothesis that the promoter has got two specific sites of binding, one for each TF, and that we can sum the probabilities of binding between the RNAase and the adequat sites.

• It seems obvious that the binding sites of OmpR^* and of FliA on pFlhDC are completly different. We made the hypothesis that any pFlhDC bound to OmpR is inactivated, whether it is bound to FliA or not.

Moreover, we know that the inhibition of pFlhDC by OmpR is effective (almost) only with OmpR-P (phosphorylated). We will use in our system (specific to pFlhDC) a mutated OmpR^*, immediatly phosphorylated, or the protein EnvZ, which is known to bind to OmpR to accelerate its phosphorylation. In the latter case, thanks to [8], we will use the following hypothesis :

• The average expression of ompR ([OmpR_b]) in usual conditions⁽¹⁾ gives, with a cell volume of 10^-15 L, near 6 μM.

• The average expression of envZ ([EnvZ_b]) in usual conditions⁽¹⁾ gives near 0.18 μM.

• The calculated expression of the K_d dissociation constant, is 1.20 μM (with a standard deviation of 0.17 μM)

⁽¹⁾ High Osmolarity, with LB medium.

Resulting Equations

First, we introduce here what we assume to be in our model the involved chemical reactions. They are written in black, regards to the equations that concerns both of the alternatives.

Then, the green equations are those implemented in our simulation programs.

The blue ones are the consequences of the complexation reacions if their stady-state are immediatly reached (see Biochemical Assumptions).