Team:Paris/Modeling/Oscillations
From 2008.igem.org
(→Biochemical Assumptions) |
(→Biochemical Assumptions) |
||
| (17 intermediate revisions not shown) | |||
| Line 20: | Line 20: | ||
In the same way, a '''repressible promoter''' has got a '''basal expression''', and its expression is proportionnal to the number of '''free promoters'''. | In the same way, a '''repressible promoter''' has got a '''basal expression''', and its expression is proportionnal to the number of '''free promoters'''. | ||
| - | + | Generally, the amount of a ''transcription factor'' is far superior than the amount of the corresponding promoter, even if it binds to several promoters (see the [[Team:Paris/Modeling/Programs|''complexation equation'' ]]). But, ''in contrario'', we have to take into acount that if several ''transcription factors'' bind to a given promoter, those several complexations are in competition. | |
| - | + | To treat this phenomenon, we must know if a reaction is ''predominant'', or if all the steady-states are reached "at the same time". We made the following hypothesis : | |
| - | + | * The contribution of the two inducers FliA and FlhDC on ''pFlhB'' are synthetised by a ''' ''SUM'' logical gate''' : that corresponds to the biological hypothesis that the promoter has got two specific sites of binding, one for each ''TF'', and that we can sum the probabilities of binding between the RNAase and the adequat sites. | |
| - | + | * It seems obvious that the binding sites of OmpR<sup>*</sup> and of FliA on pFlhDC are completly different. We made the hypothesis that any pFlhDC bound to OmpR is inactivated, whether it is bound to FliA or not. | |
| - | + | For the inhibition of the action of TetR on pTet by aTc, we suppose that the concentration of aTc in the cells is the same as the concentration in the input medium of the chemostat (as for the [[Team:Paris/Modeling/Programs#Induction_for_the_caracterisations|induction for the caracterisations]]) | |
| + | |||
| + | Moreover, we know that the inhibition of pFlhDC by OmpR is effective (almost) only with OmpR_-_P (phosphorylated). We will use in our system (specific to pFlhDC) a mutated OmpR<sup>*</sup>, ''immediatly'' phosphorylated, or the protein EnvZ, which is known to bind to OmpR to accelerate its phosphorylation. | ||
| + | In the latter case, thanks to [[Team:Paris/Modeling/Bibliography|[8]]], we will use the following hypothesis : | ||
| + | |||
| + | * The average expression of ompR ([OmpR<sub>''b''</sub>]) in ''usual conditions''<sup>(1)</sup> gives, with a cell volume of 10<sup>-15</sup> L, near 6 μM. | ||
| + | |||
| + | * The average expression of envZ ([EnvZ<sub>''b''</sub>]) in ''usual conditions''<sup>(1)</sup> gives near 0.18 μM. | ||
| + | |||
| + | * The calculated expression of the ''K<sub>d</sub>'' dissociation constant, is 1.19 μM (with a standard deviation of 0.15 μM) ; we will directly use it as the ''K<sub>d</sub><sup>eff</sup>'' (see [[Team:Paris/Modeling/Programs#Equilibrium_of_a_Complex|equilibrium of a complex]]) | ||
| + | |||
| + | from now on, we will simply assume that the notation ''OmpR<sup>*</sup>'' is equivalent to OmpR_-_P or OmpR_-_Env, treating the phosphorylation as immmediate, for both ways. | ||
| + | |||
| + | |||
| + | <sup>(1)</sup> High Osmolarity, with LB medium. | ||
| + | |||
| + | ==Resulting Equations== | ||
| - | + | First, we introduce here what we assume to be in our model '''the involved chemical reactions'''. They are written in '''black''', regards to the equations that concerns both of the [[Team:Paris/Modeling/Oscillations#The_Circuit|alternatives]]. The lighter colors represent the second alternative, with EnvZ instead of OmpR<sup>*</sup>. | |
| - | + | Then, the '''green''' equations are those implemented in our [[Team:Paris/Modeling/Codes|simulation programs]]. | |
| - | The ''' | + | The '''blue''' ones are the consequences of the [[Team:Paris/Modeling/Programs|''complexation reactions'']] if their stady-state are immediatly reached (see [[Team:Paris/Modeling/Oscillations#Biochemical_Assumptions|Biochemical Assumptions]]). |
<html><iframe width="935" height="600" src="https://static.igem.org/mediawiki/2008/0/0e/Equa_Oscill.pdf" frameborder="0"></iframe></html> | <html><iframe width="935" height="600" src="https://static.igem.org/mediawiki/2008/0/0e/Equa_Oscill.pdf" frameborder="0"></iframe></html> | ||
|}<br style="clear:both" /> | |}<br style="clear:both" /> | ||
Latest revision as of 17:29, 12 October 2008
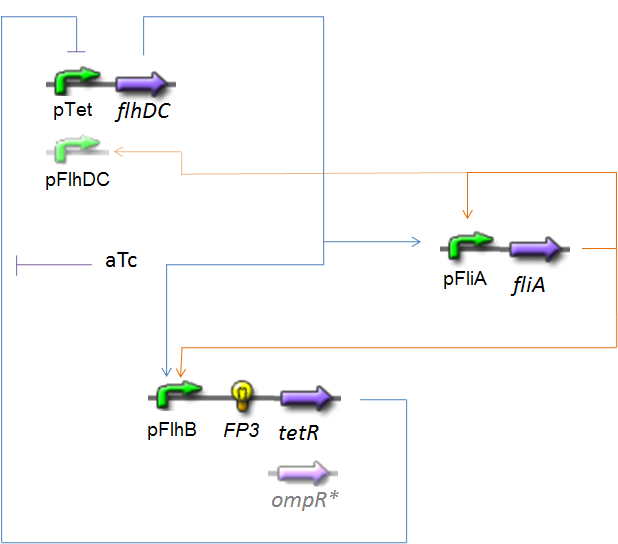
OscillationsThe CircuitWe just keep here the following circuit, constituing the Oscillations. The gene FP3 codes for the third reporter protein we will use in our final system. We have two alternatives for the promoter before flhDC : pTet or pFlhDC. These two alternatives are both studied in what follows.
Biochemical AssumptionsWe do not take into acount the phenomenon of translation : we consider the transduction as leading directly to the production of the protein (see however considerations on RBS). We assume that the expression rate of an inducible promoter is proportionnal to the number of created complexes promoter-inducer. In the same way, a repressible promoter has got a basal expression, and its expression is proportionnal to the number of free promoters. Generally, the amount of a transcription factor is far superior than the amount of the corresponding promoter, even if it binds to several promoters (see the complexation equation ). But, in contrario, we have to take into acount that if several transcription factors bind to a given promoter, those several complexations are in competition. To treat this phenomenon, we must know if a reaction is predominant, or if all the steady-states are reached "at the same time". We made the following hypothesis :
For the inhibition of the action of TetR on pTet by aTc, we suppose that the concentration of aTc in the cells is the same as the concentration in the input medium of the chemostat (as for the induction for the caracterisations) Moreover, we know that the inhibition of pFlhDC by OmpR is effective (almost) only with OmpR_-_P (phosphorylated). We will use in our system (specific to pFlhDC) a mutated OmpR*, immediatly phosphorylated, or the protein EnvZ, which is known to bind to OmpR to accelerate its phosphorylation. In the latter case, thanks to [8], we will use the following hypothesis :
from now on, we will simply assume that the notation OmpR* is equivalent to OmpR_-_P or OmpR_-_Env, treating the phosphorylation as immmediate, for both ways.
Resulting EquationsFirst, we introduce here what we assume to be in our model the involved chemical reactions. They are written in black, regards to the equations that concerns both of the alternatives. The lighter colors represent the second alternative, with EnvZ instead of OmpR*. Then, the green equations are those implemented in our simulation programs. The blue ones are the consequences of the complexation reactions if their stady-state are immediatly reached (see Biochemical Assumptions).
|
 "
"