Team:BCCS-Bristol/Modeling
From 2008.igem.org
(→Transport) |
(→Transport) |
||
| Line 67: | Line 67: | ||
over time. A delta input of size 50 was used and the concentration distribution calculated over | over time. A delta input of size 50 was used and the concentration distribution calculated over | ||
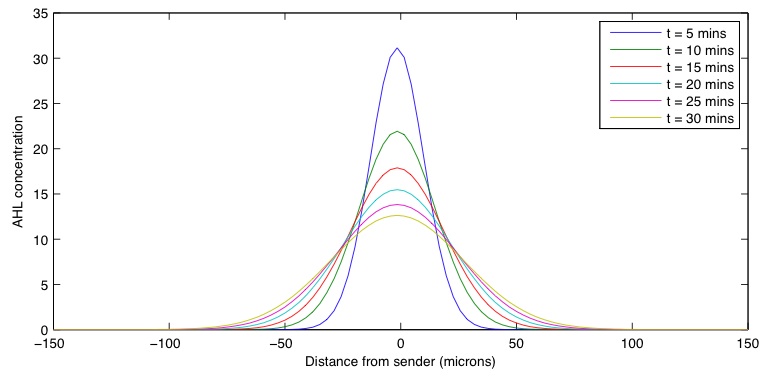
a 30 minute period. Figure 2 shows the distribution at 5 minute intervals. A value of 0.23 s<sup>-1</sup> | a 30 minute period. Figure 2 shows the distribution at 5 minute intervals. A value of 0.23 s<sup>-1</sup> | ||
| - | was selected for the diffusion co-efficient | + | was selected for the diffusion co-efficient. |
As we do not know the maximal expression level C<sub>pMax</sub> of the response regulator CpxR it | As we do not know the maximal expression level C<sub>pMax</sub> of the response regulator CpxR it | ||
was difficult to estimate the rate that an individual cell would produce AHL. For this reason | was difficult to estimate the rate that an individual cell would produce AHL. For this reason | ||
we attempted to concentrate on understanding the distance over which a threshold value was | we attempted to concentrate on understanding the distance over which a threshold value was | ||
| - | exceeded. The receiver GRN has been shown to be sensitive to low levels of AHL, see | + | exceeded. The receiver GRN has been shown to be sensitive to low levels of AHL, see previous section, and so we assumed a large response would occur at concentrations of 3 and greater. |
| - | + | ||
[[Image:BCCS-Modelling-Transport.jpg|center|thumb|400px|'''Figure 2: Transport Results''' - Concentration distribution over a 30 min period for an initial delta function input at 0 of 50]] | [[Image:BCCS-Modelling-Transport.jpg|center|thumb|400px|'''Figure 2: Transport Results''' - Concentration distribution over a 30 min period for an initial delta function input at 0 of 50]] | ||
Revision as of 14:19, 22 October 2008
|
Approach
Due to the nature of this project, a wide range of modelling techniques are required to help understand ideas and guide experimentation in the wet lab. The reason for this is that in addition to the creation of synthetic genetic circuits to regulate the internal state of a cell, we require the cell to physically interact with the environment in such a way that by bringing a large number of them together, all following to same rules, emergent behaviours are exhibited - the ultimate outcome of the project. To do this it is necessary to take into consideration the movement (chemotaxis) and physical force exerted between large numbers of cells in an environment as well as other aspects such as chemical diffusion, fluid dynamics and individual cell states.
For these reasons we will be developing two types of model, an internal representation of a single bacterium using differential equations, and a external representation of the system as a whole using computerised stochastic agents. This will allow us to gain a better understanding of the different aspects of the project in a manageable way. Once these models have been completed, in an attempt to combine the advantages of each, both will be combined to give a holistic view of the modelling from a single cell to the whole population.
Both types of model will make heavy use of computing resources. We are looking to utilise MATLAB for tasks such as numerical integration and statistical analysis and Java for the development of a stochastic agent based framework that will allow us to simulate bacterial chemotaxis, physical interactions between bacteria/particles and chemical fields exhibiting diffusion. The simulation environment will form the majority of the modelling work and once we can incorporate the GRN dynamics within each bacterium (agent) we hope to be able to perform virtual experiments that mimic those in the wet lab.
The major limitiation of this approach is that the simulation of huge numbers of bacteria requires huge amounts of computing power. This means that for any reasonably sized simulations we will have to seriously consider optimising our code to make most efficient use of local resources (e.g. multi-threading for multiple processor/core machines) and for larger simulations allow for execution on distributed computing architectures. With this in mind we are aiming to gain access to the [http://www.acrc.bris.ac.uk/acrc/hpc.htm Blue Crystal] high performance computing cluster at the university to attempt some large scale simulations.
Models
 |  |  |
| | | |
| To understand the dynamics of genetic networks that we design, differental equations are used to model the changes in concentration of mRNA and proteins. | With the project requiring global behaviour to emerge via the physical en masse movement of bacteria, stochastic agent based simulations are used to investigate the viability and limits of different approaches. | With the aim of improving simulation accuracy this model integrates the intercellular GRN dynamics with the extra-cellular interactions of the stochastic agent based simulation. |
Results
Gene Regulatory Network
Sender
To assess the sender GRN we were interested in how the strength of the response regulator CpMax affects the overall dynamics and the final output of AHL. For a CpMax range of [0.1, 100] the qualitative behaviour of the GRN was the same, shown in Figure 1a for a CpMax value of 5 molecules per cell. Both GFP and LuxI proteins rise rapidly in the first hour, while CpxR and LuxI mRNA reaches a maximum after 60 minutes. The final LuxI mRNA concentration is low, causing the rate of increase in LuxI protein to slow towards the end of the simulation. In contrast, both mRNA and protein concentrations of GFP continue to increase rapidly for the duration.
Figure 1b shows how the initial CpMax value effects AHL output over time. The behaviour is seen to be asymptotic, tending to a final concentration after approximately 400 minutes. The relationship between CpMax and AHL appears to be non-linear, with a rapid increase seen between 0.1 and 1. After this point the rate seems to slows, reaching a maximum near 4300. The huge variability in output AHL, even when the initial CpMax value is only varied by a small amount, makes it difficult to estimate a realistic output for a single cell. Experimental techniques would need to be used to refine the accuracy of these results and allow for an appropriate CpMax value to be chosen. Overall, the GRN exhibits the correct dynamics, giving a sizeable AHL production in the presence of a CpxR response.
Transport
For the transport aspect of the system we investigated how the concentration distribution varied over time. A delta input of size 50 was used and the concentration distribution calculated over a 30 minute period. Figure 2 shows the distribution at 5 minute intervals. A value of 0.23 s-1 was selected for the diffusion co-efficient. As we do not know the maximal expression level CpMax of the response regulator CpxR it was difficult to estimate the rate that an individual cell would produce AHL. For this reason we attempted to concentrate on understanding the distance over which a threshold value was exceeded. The receiver GRN has been shown to be sensitive to low levels of AHL, see previous section, and so we assumed a large response would occur at concentrations of 3 and greater.
Reciever
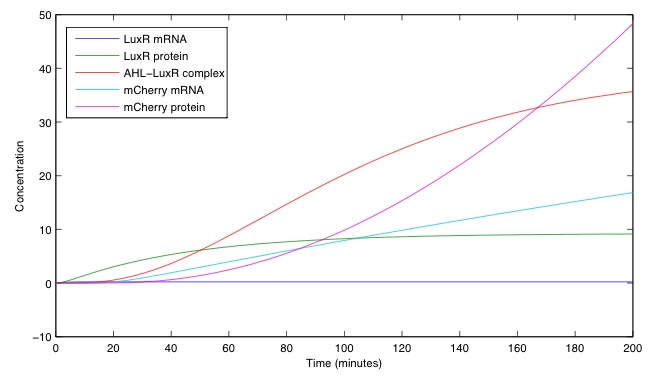
For the receiver we wanted to understand how varying AHL concentration altered output of our signalling protein mCherry. This relationship is shown in Figure 3b. Availability of any AHL causes a large increase in mCherry output, however, the rate of increase decays exponentially. Output increases very little once a concentration of 3 molecules per cell has been reached. The internal dynamics of the receiver GRN is shown in Figure 3a for an input AHL concentration of 3. From an initial starting condition with all other states at 0, the LuxR protein can be seen to rise to a stable maximum concentration of 9 molecules per cell after 100 minutes. The LuxR–AHL complex also appears to have asymptotic behaviour tending to a concentration of approximately 40 molecules per cell. Production of mCherry protein occurs rapidly once LuxR concentration reaches a suitable level after 30 minutes. As LuxR in a living cell would be maintained at a high level due to the constitutive promoter, the response would normally be much quicker. With microscopes able to register individual mCherry proteins, the large response to small AHL increases means the GRN behaves as we require, producing a visible signal quickly.
Stochastic Agent Based Model
Basic Chemotaxis Model
Comparing Construction Rules
Bacteria to Particle Adhesion
Simulation Movies
All simulation movies have been exported from BSim and require [http://www.apple.com/quicktime Quicktime] in order to be viewed. They have each been compressed to reduce their size, however, please be patient when downloading as some are still quite large.
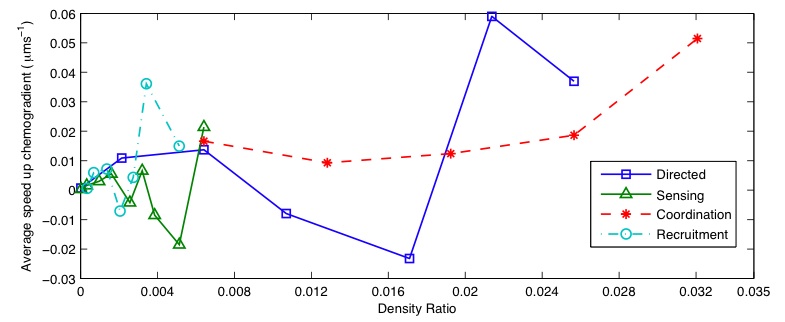
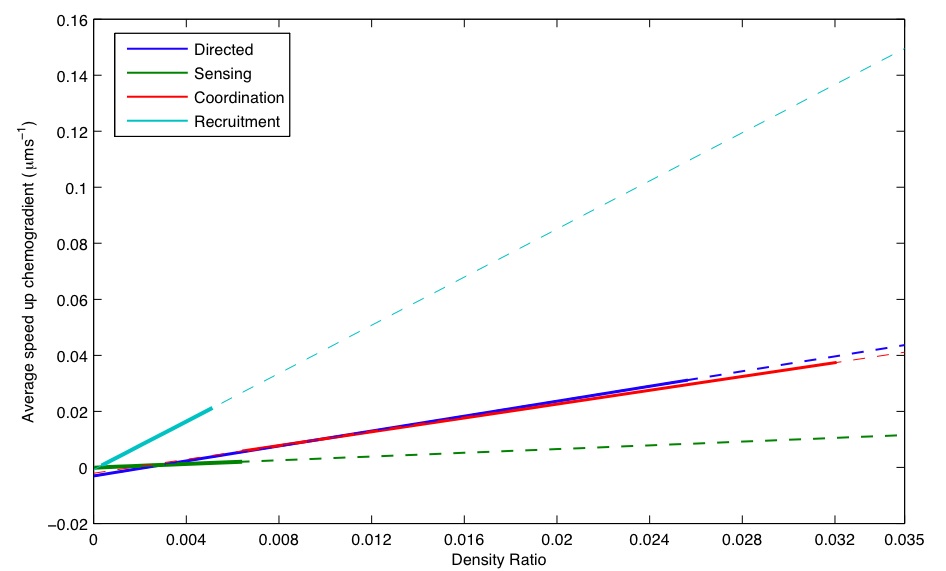
- [http://2008sw.igem.org/bccs_bristol/media/BCCS-Modelling-Basic_Chemotaxis.mov Basic Chemotaxis] - Demonstrates bacteria performing chemotaxis towards a chemoattractant (increasing to the right). The trace displays the average position of all bacteria. This can be seen to move in a random manner with a bias towards the chemoattractant.
- [http://2008sw.igem.org/bccs_bristol/media/BCCS-Modelling-Direct_Movement.mov Directed Movement] - Shows a particle placed in a swarm of bacteria following the chemotactic gradient. Collisions between bacteria and the particle result in a net movement up the chemotactic gradient.
- [http://2008sw.igem.org/bccs_bristol/media/BCCS-Modelling-Coordination.mov Short Range Co-ordination] - Bacteria are initially not responsive to the chemoattractant. On coming into contact with the particle, a bacterium's chemotactic response is switched on. At the same time a quorum based signal is produced by the bacteria that are in contact with the particle. Neighbouring bacteria switch from a random walk to a chemotactic response on sensing the quorum based signal.
- [http://2008sw.igem.org/bccs_bristol/media/BCCS-Modelling-Recruitment.mov Long Range Recruitment] - The bacteria act as above but on contact with the particle also produce a long range chemotactic based signal, recruiting distant bacteria towards the particle.
- [http://2008sw.igem.org/bccs_bristol/media/BCCS-Modelling-Adhesion.mov Bacteria to Particle Adhesion] - Bacteria are adhered to the particle and follow a chemotactic gradient.
Software Download
To download both compiled versions of BSim and the source code for both BSim and the MATLAB GRN models see our Software Download Page.
Modelling Notebook
- Progress Report - To track our progress see our weekly reports. These let you know what we have been up to, including comments on the reasons behind any important decisions that were made.
- Modelling Parameters - Full listings of all parameters investigated for the modelling part of the project, with values that have been chosen, reasons for their selection and references to the original sources.
- To Do List - List of items that need to be done on the modelling and simulation.
- Batch Simulations - Outline of all simulations we intend to run.
 "
"