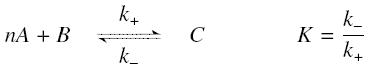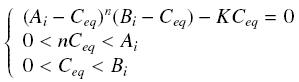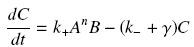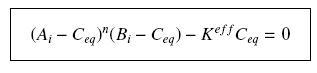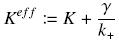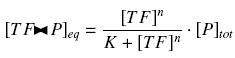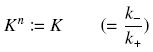|
Complexations
Quasi Steady-State Hypothesis
The problem is the following : for given values of molecules A and B at initial state, what is the final state if A and B can bind together ? With the answer at this question, we would be able to treat separately each step of our system as an "independant module", taking as input values of Ai and Bi and giving as output values of Aeq, Beq and Complexeq. By doing so, we are doing the hypothesis of quasi steady-state because it implies that the complexations reach immediatly their equilibrium. The kinetical behaviour of the final model is nevertheless taking into account, because the reactions of productions are considered slower, and the characterization would give us their speed, regards to the ratio with the (known) value of the degradation γ
Basical Complexations
The first hypothesis is that a complexation reaction is fully determined by the following :
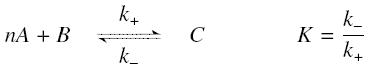
and that the rates k+ et k- stay constant under all conditions. Then, the second hypothesis is that these equations are (kinetically speaking) elementary :
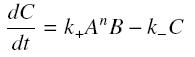 and at steady-state :
and at steady-state : 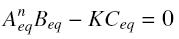
Thus, the solution is (at least if we take the smallest real root of the equation, it is useless to demonstrate the unicity, or even the existence, of such a solution) :
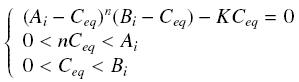
Equilibrium of a Complex
Now, if we imagine a given amount of Ai and Bi, that are calculated as their equilibrium without taking acount of their complexation (but, for instance, of other interactions, productions and disappearance), and that the produced complex C disappears along time with a degradation rate γ, we get :
so that the equilibrium gives :
with
Hill Functions
The previous system of complexation applied in particular to the association of the Promoters (P) and its Transcription Factor (TF).
Because the promoters on a "low copy plasmid" exists in the cell in ten exemplaries, in contrary to a protein, which, as long as it is produced (even weakly) exists in thousands of exemplaries, we assume can the quantities of TF and P are different by several orders of magnitude. Then, with the previous notations, if A, B and C stands respectively for TF, P and the complex TF><P, we will get
that we can easily solve with :
Depending to the order n (also called cooperativity, because it correponds to the possibilities of the transcription factor to binds in a group on the promoter), this function is a sigmoïd, known as the Hill function. The parameter K , called activation constant, is often replaced in the previous expression by the following notation
It simplifies the manipulations of the expression ; we can notice that K represents now the amount of TF needed to bind half of the total P in the cell.
|
 "
"