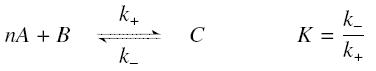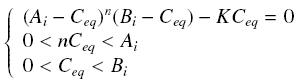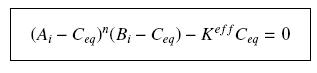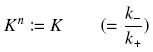Team:Paris/Modeling/More From2Ode Math
From 2008.igem.org
(Difference between revisions)
(New page: {{Paris/Menu}} {{Paris/Header|Complexations}} ==Quasi Steady-State Hypothesis== The problem is the following : for given values of molecules A and B at initial state, what is the final ...) |
(→Hill Functions) |
||
| (18 intermediate revisions not shown) | |||
| Line 5: | Line 5: | ||
==Quasi Steady-State Hypothesis== | ==Quasi Steady-State Hypothesis== | ||
| - | The problem is the following : for given values of molecules A and B at initial state, what is the final state if A and B can bind together ? With the answer at this question, we would be able to treat separately each step of our system as an "independant module", taking as input values of A<sub>i</sub> and B<sub>i</sub> and giving as output values of A<sub>eq</sub>, B<sub>eq</sub> and Complex<sub>eq</sub>. By doing so, we are doing the hypothesis of '''quasi steady-state''' because it implies that the complexations | + | The problem is the following : for given values of molecules A and B at initial state, what is the final state if A and B can bind together ? With the answer at this question, we would be able to treat separately each step of our system as an "independant module", taking as input values of A<sub>i</sub> and B<sub>i</sub> and giving as output values of A<sub>eq</sub>, B<sub>eq</sub> and Complex<sub>eq</sub>. By doing so, we are doing the hypothesis of '''quasi steady-state''' because it implies that the complexations reach immediatly their equilibrium. The kinetical behaviour of the final model is nevertheless taking into account, because the reactions of productions are considered slower, and the characterization would give us their speed, regards to the ratio with the (known) value of the degradation γ |
| - | == | + | ==Complexation Reaction== |
The first hypothesis is that a complexation reaction is fully determined by the following : | The first hypothesis is that a complexation reaction is fully determined by the following : | ||
| Line 15: | Line 15: | ||
and that the rates k<sub>+</sub> et k<sub>-</sub> stay constant under all conditions. Then, the second hypothesis is that these equations are (kinetically speaking) ''elementary'' : | and that the rates k<sub>+</sub> et k<sub>-</sub> stay constant under all conditions. Then, the second hypothesis is that these equations are (kinetically speaking) ''elementary'' : | ||
| - | <center> [[Image:kinhill.jpg| | + | <center> [[Image:kinhill.jpg|150px]] </center> |
| - | and at steady-state : <center> [[Image:sshill.jpg]] </center> | + | and at steady-state : <center> [[Image:sshill.jpg|150px]] </center> |
Thus, the solution is (at least if we take the smallest real root of the equation, it is useless to demonstrate the unicity, or even the existence, of such a solution) : | Thus, the solution is (at least if we take the smallest real root of the equation, it is useless to demonstrate the unicity, or even the existence, of such a solution) : | ||
| Line 26: | Line 26: | ||
Now, if we imagine a given amount of ''A<sub>i</sub>'' and ''B<sub>i</sub>'', that are calculated as their equilibrium without taking acount of their complexation (but, for instance, of other interactions, productions and disappearance), and that the produced complex C disappears along time with a ''degradation rate γ'', we get : | Now, if we imagine a given amount of ''A<sub>i</sub>'' and ''B<sub>i</sub>'', that are calculated as their equilibrium without taking acount of their complexation (but, for instance, of other interactions, productions and disappearance), and that the produced complex C disappears along time with a ''degradation rate γ'', we get : | ||
| - | [[Image:GammaC.jpg|center| | + | [[Image:GammaC.jpg|center|180px]] |
| - | so that the equilibrium gives : | + | <center> |
| + | so that the equilibrium gives : [[Image:EqGammaC.jpg|250px]] with [[Image:Keff.jpg|100px]] | ||
| + | </center> | ||
| - | + | We will obviously be looking for the parameter K<sup>eff</sup>, which avoid us to evaluate the unavailable k<sub>+</sub> | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
==Hill Functions== | ==Hill Functions== | ||
| Line 46: | Line 44: | ||
that we can easily solve with : | that we can easily solve with : | ||
| - | [[Image:reshill.jpg|center| | + | [[Image:reshill.jpg|center|200px]] |
Depending to the order ''' ''n'' ''' (also called ''cooperativity'', because it correponds to the possibilities of the transcription factor to binds in a group on the promoter), this function is a ''sigmoïd'', known as the ''Hill function''. The parameter ''' ''K'' ''', called ''activation constant'', is often replaced in the previous expression by the following notation | Depending to the order ''' ''n'' ''' (also called ''cooperativity'', because it correponds to the possibilities of the transcription factor to binds in a group on the promoter), this function is a ''sigmoïd'', known as the ''Hill function''. The parameter ''' ''K'' ''', called ''activation constant'', is often replaced in the previous expression by the following notation | ||
| - | [[Image:changeK.jpg|center| | + | [[Image:changeK.jpg|center|150px]] |
It simplifies the manipulations of the expression ; we can notice that ''' ''K'' ''' represents now the amount of ''TF'' needed to bind half of the total ''P'' in the cell. | It simplifies the manipulations of the expression ; we can notice that ''' ''K'' ''' represents now the amount of ''TF'' needed to bind half of the total ''P'' in the cell. | ||
[[Image:hilldef.jpg|center|300px]] | [[Image:hilldef.jpg|center|300px]] | ||
| + | |||
| + | <br> | ||
| + | |||
| + | <center> | ||
| + | [[Team:Paris/Modeling/FromMolReactToNLOde| < Back - to "From Molecular Reactions to Non-Linear ODEs"]]| | ||
| + | </center> | ||
Latest revision as of 00:06, 29 October 2008
 "
"