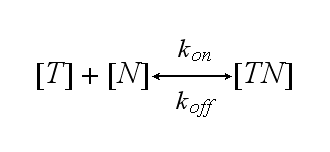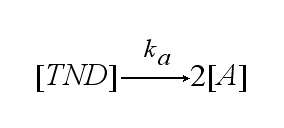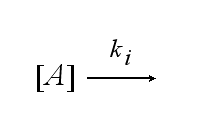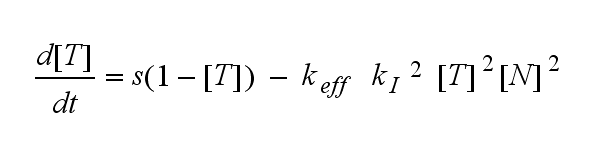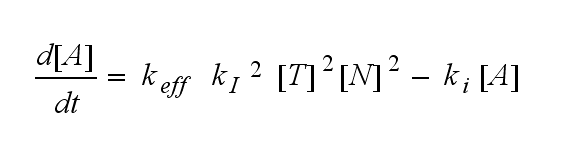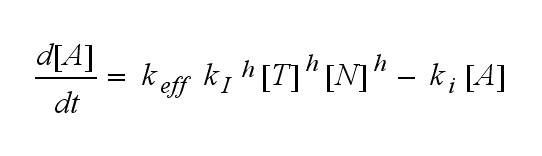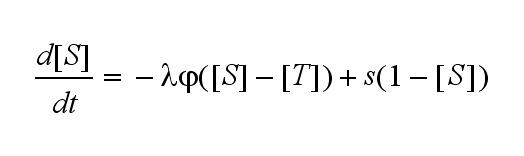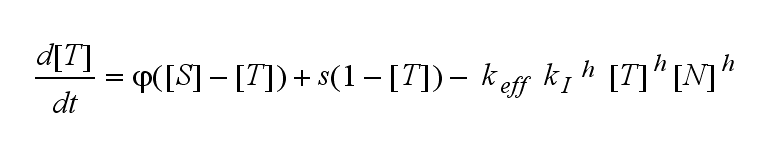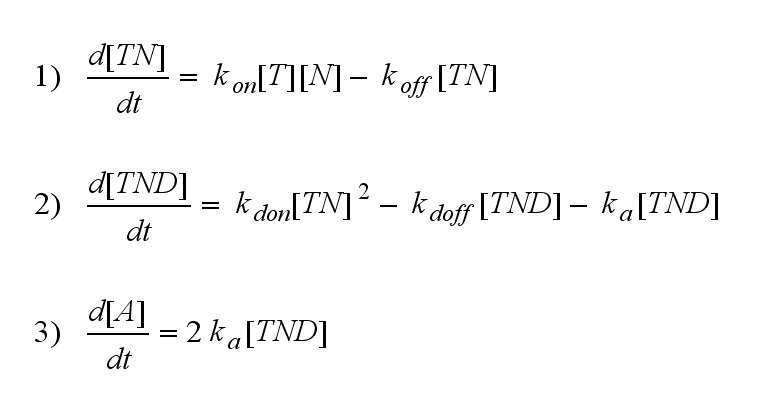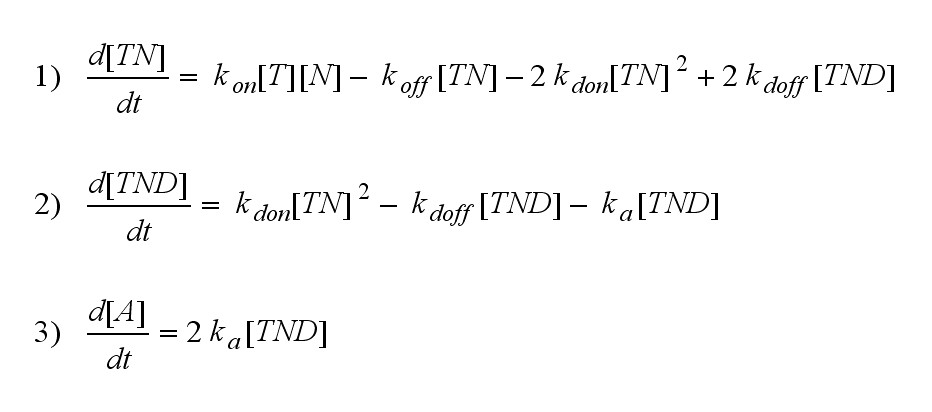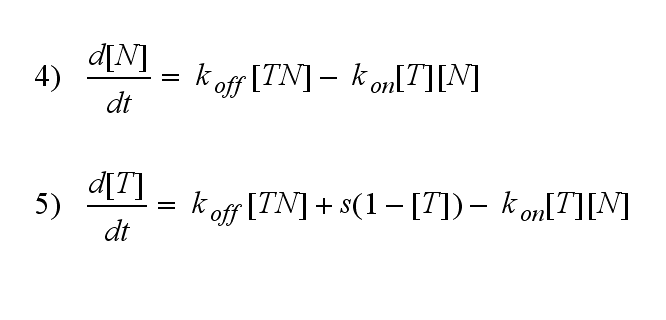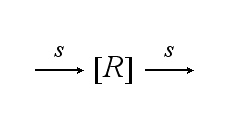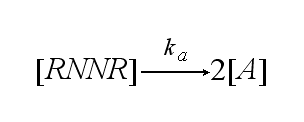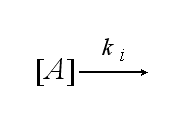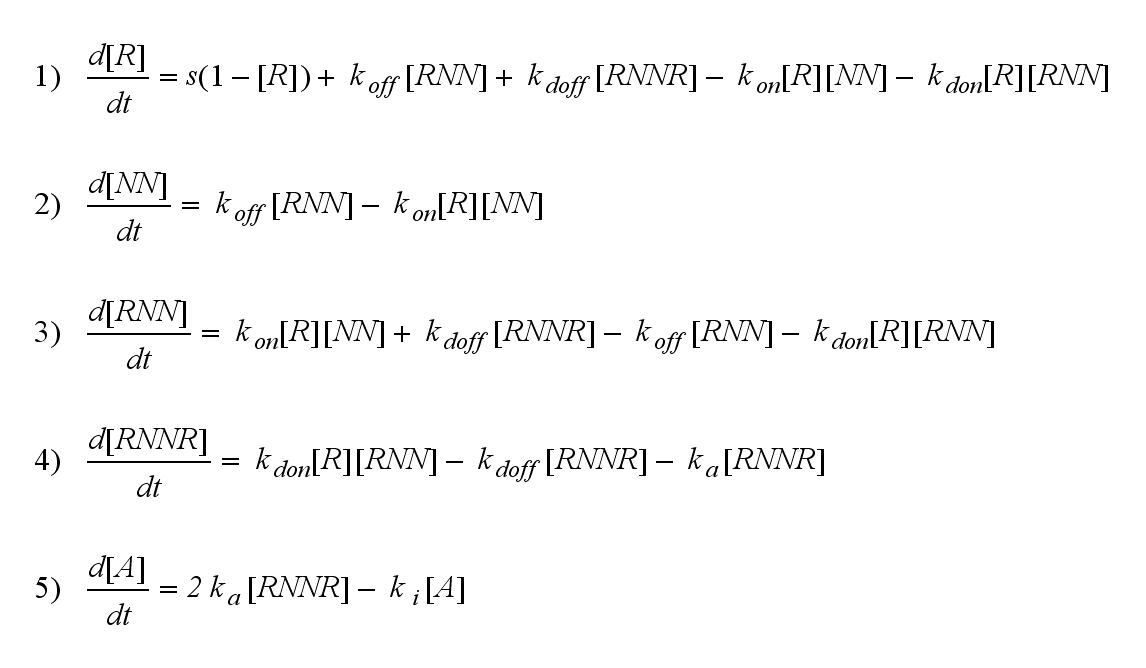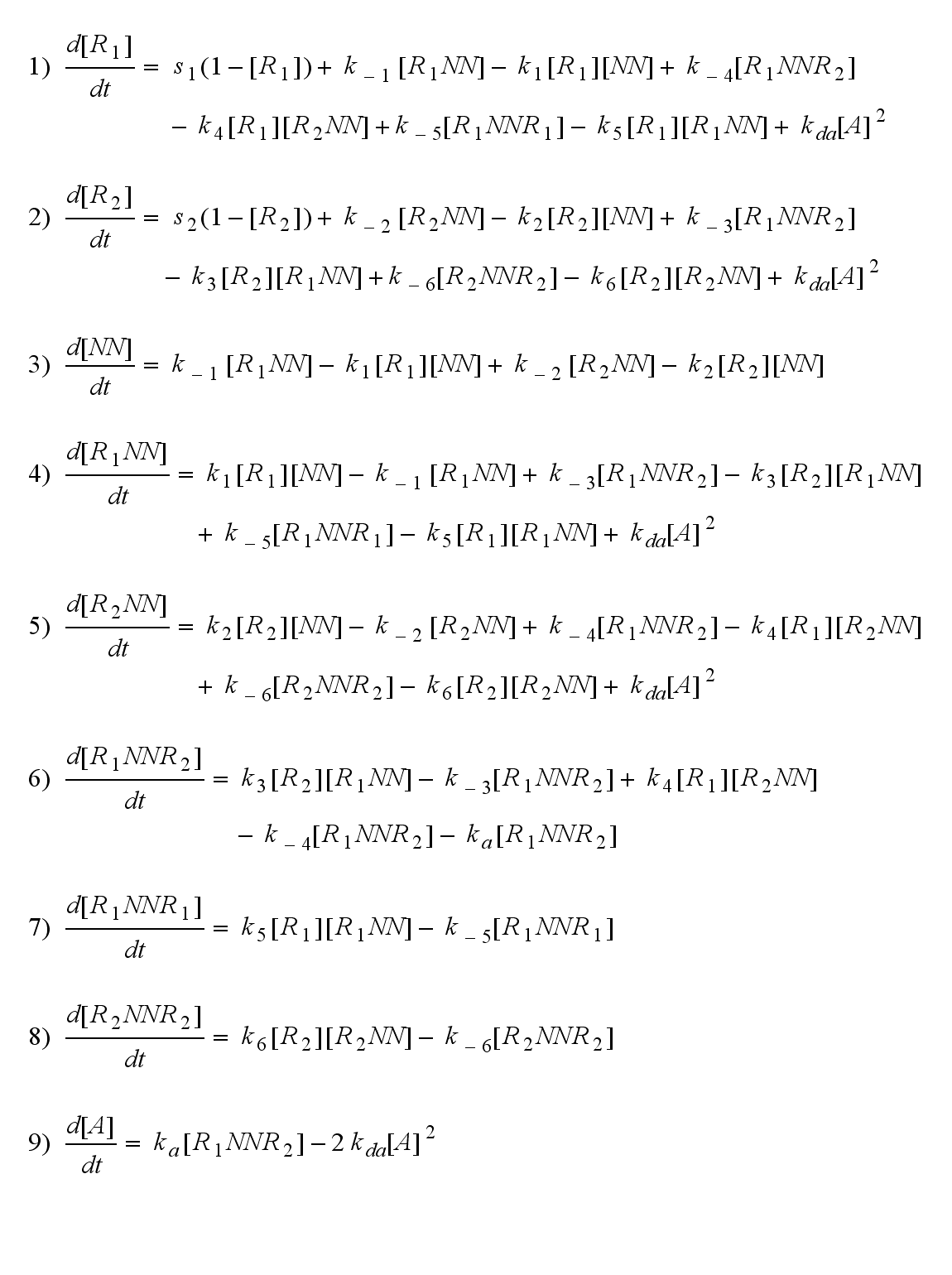Team:Freiburg/Modeling
From 2008.igem.org
m |
m |
||
| (6 intermediate revisions not shown) | |||
| Line 56: | Line 56: | ||
<br><br> | <br><br> | ||
| - | After activation, the TCR is | + | After activation, the TCR is internalized with rate '''k'''<sub>i</sub> and does not take part anymore in the extracellular signaling : |
<br> | <br> | ||
[[Image:Freiburg2008_RKM1int.png|150px]] | [[Image:Freiburg2008_RKM1int.png|150px]] | ||
| Line 93: | Line 93: | ||
The activity has a maximum a short time after NIP presentation and decreases as the active TCRs are internalized and as the free membrane TCR amount is decreasing. It is remarkable that the response never decreases to complete zero, even for very high internalization rates and in a long time course. | The activity has a maximum a short time after NIP presentation and decreases as the active TCRs are internalized and as the free membrane TCR amount is decreasing. It is remarkable that the response never decreases to complete zero, even for very high internalization rates and in a long time course. | ||
<br><br> | <br><br> | ||
| - | <h2>Extensions: | + | <h2>Extensions: Ultrasensitivity and biphasic kinetics</h2> |
[[media:Freiburg2008_M1_Xten.m|''matlab m-file'']]<br> | [[media:Freiburg2008_M1_Xten.m|''matlab m-file'']]<br> | ||
<h3>Ultrasensitivity</h3> | <h3>Ultrasensitivity</h3> | ||
| Line 144: | Line 144: | ||
</tr> | </tr> | ||
</table> | </table> | ||
| - | The x-axis represents the time course of the activity, the y-axis represents both parameters φ ( = y) and λ ( = 2 - y). So each black line in the plot is a time course of the TCR activity for a different φ and λ. The z-axis is the response intensity. With increasing exchange between the interface and spare pool, more TCRs switch to the binding state, hence more TCRs can bind NIP. As a consequence the active TCR density is higher | + | The x-axis represents the time course of the activity, the y-axis represents both parameters φ ( = y) and λ ( = 2 - y). So each black line in the plot is a time course of the TCR activity for a different φ and λ. The z-axis is the response intensity. With increasing exchange between the interface and spare pool, more TCRs switch to the binding state, hence more TCRs can bind NIP. As a consequence the active TCR density is higher than for a low exchange. <br> |
<h2>Correction terms</h2> | <h2>Correction terms</h2> | ||
[[media:Freiburg2008_M1_Corrected.m|''matlab m-file'']]<br><br> | [[media:Freiburg2008_M1_Corrected.m|''matlab m-file'']]<br><br> | ||
| Line 192: | Line 192: | ||
</tr> | </tr> | ||
</table> | </table> | ||
| - | After NIP addition the TCR activity rises to a maximum and decreases as active receptors are internalized and the NIP amount is used up. The free receptor density recovers due to permanent expression of new receptors which are | + | After NIP addition the TCR activity rises to a maximum and decreases as active receptors are internalized and the NIP amount is used up. The free receptor density recovers due to permanent expression of new receptors which are built into the membrane. |
<br> | <br> | ||
<h1>Receptor dimerization model II</h1> | <h1>Receptor dimerization model II</h1> | ||
| Line 391: | Line 391: | ||
<font color="#336600"> | <font color="#336600"> | ||
s = 0.1; % turnover rate | s = 0.1; % turnover rate | ||
| - | kon : | + | kon : 3 % receptor-NIP binding rate |
koff = 0.1; % receptor-NIP dissociating rate | koff = 0.1; % receptor-NIP dissociating rate | ||
kdon = 1; % receptor-NIP dimerization rate | kdon = 1; % receptor-NIP dimerization rate | ||
| Line 452: | Line 452: | ||
<tr> | <tr> | ||
<td> | <td> | ||
| - | [[image: | + | [[image:Freiburg2008_MSRSp1.png|thumb|left|400px|'''Figure 16:''' Involved receptor densities in time]] |
Assuming equal parameters for R<sub>1</sub> and R<sub>2</sub> leads to equal densities of both; shown through one plot curve for each uniform density (free receptor density, monomeric density, dimeric density) of R<sub>1</sub> and R<sub>2</sub> | Assuming equal parameters for R<sub>1</sub> and R<sub>2</sub> leads to equal densities of both; shown through one plot curve for each uniform density (free receptor density, monomeric density, dimeric density) of R<sub>1</sub> and R<sub>2</sub> | ||
</td> | </td> | ||
| Line 549: | Line 549: | ||
</tr> | </tr> | ||
</table> | </table> | ||
| + | <br><br> | ||
<h1>Matlab m-files</h1> | <h1>Matlab m-files</h1> | ||
*[[media:Freiburg2008_M1_Basic.m|Basic dimerization model 1]]<br> | *[[media:Freiburg2008_M1_Basic.m|Basic dimerization model 1]]<br> | ||
Latest revision as of 18:06, 8 March 2009
|
Modeling |
_modeling
IntroductionDimerization of the extracellular receptor domains is an important necessity for the functionality of our Modular Synthetic Receptor System. Presenting the system a stimulus in the form of spatial arranged ligands results in dimerization of the extracellular domains and thus the corresponding intracellular parts such as the split lactamase halves or split fluorescent proteins complement to a measurable output. To analyze the functionality due to dimerization, first two receptor dimerization models (one T cell receptor model and one general receptor model) are introduced and discussed and then a proper model for the Modular Synthetic Receptor System is constructed.
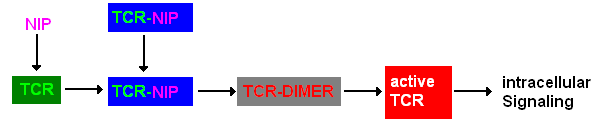
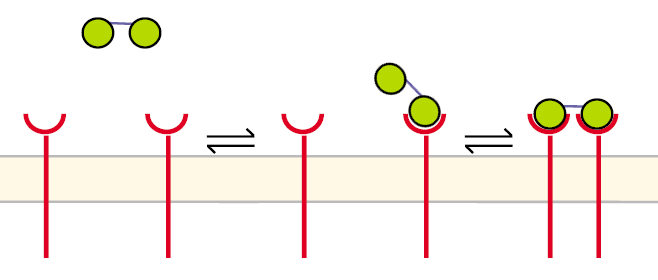
T cell receptor dimerization model Imatlab m-file Extracellular signalingA simplified pathway shows the extracellular sequence of TCR activation. After the NIP binding two complexes come together and form a dimer which then leads to activation of the TCR and further intracellular signaling and T cell activation.
Reaction kinetics
One NIP molecule (N) binds to a TCR (T) with the reaction rate kon or a TCR-NIP complex (TN) dissociates with the reaction rate koff :
Two TCR-NIP (TN) complexes dimerize to a TCR-NIP dimer (TND) with rate kdon ; the dissociation of a TCR-NIP dimer runs with rate kdoff :
In order to get active TCRs, the TCR-NIP dimer (TND) has to switch into two active TCRs (A) with rate ka :
After activation, the TCR is internalized with rate ki and does not take part anymore in the extracellular signaling :
ODEs derived from the kinetics (Details)In the following equation T represents the free TCR in the T cell membrane where keff is a combination of kdon, kdoff and ka. kI is kon/koff : TCR activity for a set of parametersThe two ODEs above of this first basic model for a set of parameters are solved numerically. They reveal the time course of the TCR activity and the time course of the unbound TCR aswell.
The activity has a maximum a short time after NIP presentation and decreases as the active TCRs are internalized and as the free membrane TCR amount is decreasing. It is remarkable that the response never decreases to complete zero, even for very high internalization rates and in a long time course.
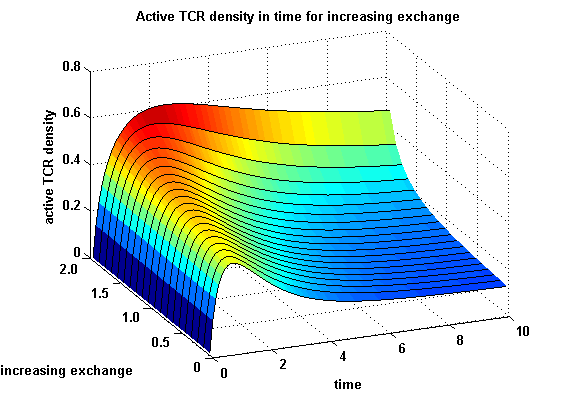
Extensions: Ultrasensitivity and biphasic kineticsUltrasensitivityThe kinetics of the TCR activation can be generalised by substituting the second order kinetic of the ligand N and the receptor T by a parameter h, which then represents the kinetic order of the system. Biphasic kinetics and parameter analysisNot all TCRs on a T cell membrane can be recruited to NIP binding as a cell´s membrane contains several transmembrane proteins whose size can avoid a TCR-NIP formation when they surround a TCR and make the approaching of the NIP to the binding side of the TCR impossible. Considerating this spatial barriers leads to the idea of a TCR which can switch between two states, one binding state and one non-binding state. Hence a introduction of two different pools of TCRs into the model is appropriate. If a TCR is not available for a NIP molecule, thus it is in the non-binding state, it belongs to the so called spare pool, whereby TCRs belonging to the so called interface pool are in the binding state and can be accessed by the NIP molecule. Moreover the spare pool is in dynamical exchange with the interface pool, so non-binding TCRs can become binding TCRs. This exchange is regulated through the parameter λ, a ratio between the spare and the interface pool and φ, the exchange rate constant. S is the spare pool TCR density and T the TCR density of the interface pool. A represents the active TCR density. So the full model I equations are: TCR activity dependent on exchange rate φ and ratio λ :
The x-axis represents the time course of the activity, the y-axis represents both parameters φ ( = y) and λ ( = 2 - y). So each black line in the plot is a time course of the TCR activity for a different φ and λ. The z-axis is the response intensity. With increasing exchange between the interface and spare pool, more TCRs switch to the binding state, hence more TCRs can bind NIP. As a consequence the active TCR density is higher than for a low exchange. Correction termsmatlab m-file
but :
Furthermore can be derived for the NIP density and the free TCR:
After NIP addition the TCR activity rises to a maximum and decreases as active receptors are internalized and the NIP amount is used up. The free receptor density recovers due to permanent expression of new receptors which are built into the membrane.
Receptor dimerization model IImatlab m-file Before the first step the receptors are unbound and diffuse in the cell´s membrane. The DNA-Origami binds to a receptor in the way that only one NIP molecule is connecting to one receptor. In the second step the second NIP molecule binds to the second receptor and both receptors dimerize.
Reaction kineticsThe continuous production of the cell´s receptor R with rate s is:
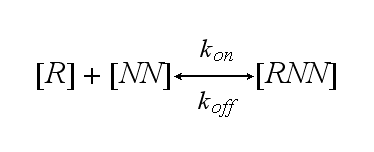
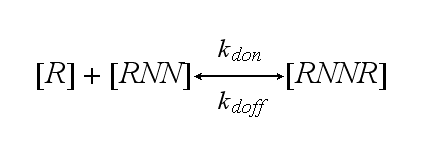
One receptor R binds to one of two NIP molecules NN of the DNA-Origami with rate kon or a receptor-NIP complex RNN dissociates with koff:
ODE derivationThe ODEs are derived from the reaction kinetics: Extracellular receptor activityFor a set of parameters the ODEs are solved and reveal amongst the other quantities the receptor densities in the time course:
The receptor activity rises after NIP addition, has a maximum and decreases due to the internalization of the active receptor. The dimer density increases fast after addition of NIP and decreases as dimers fade into active receptors.
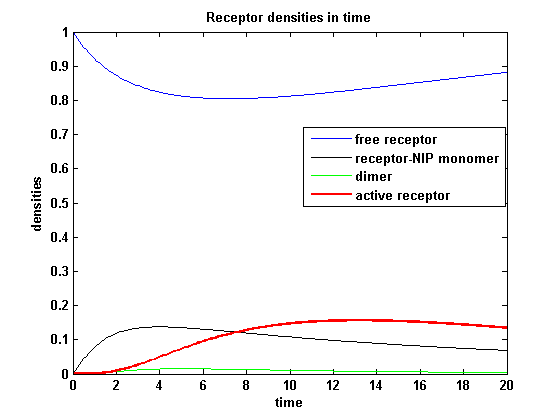
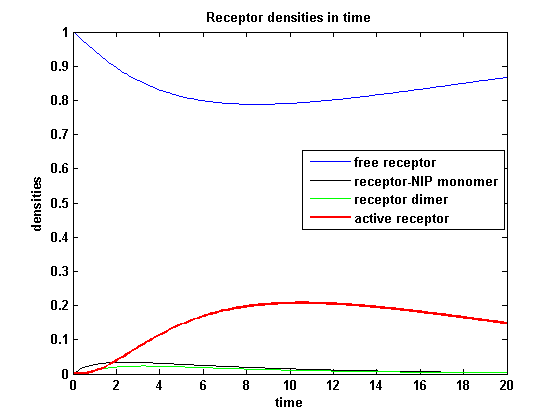
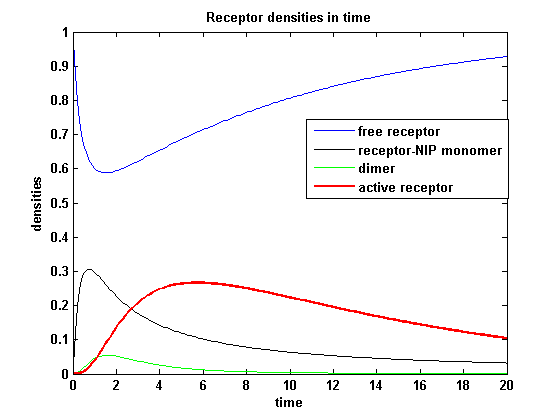
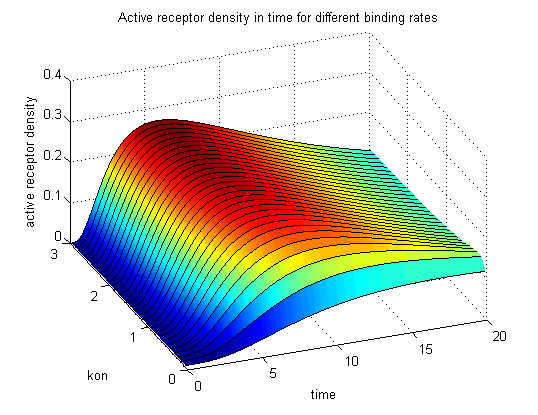
Discussion of model I and IIFor comparison, the ODEs of the corrected model 1 and model 2 are taken. The receptor NIP binding mechanism differs in the two models. Model I assumes the production of two independent receptor-NIP complexes which can dimerize after formation. In model II, dimerization happens after one of two receptors connects to the bivalent ligand . Setting several conditions unravels the consequences of this differences for the active receptor, the dimer and the receptor recovery. Different binding rates, dimerization rates and ligand amounts are used in the solutions of the model I ODEs and model II ODEs. Receptor densities dependent on binding rate konThe two model ODEs are solved for the mentioned parameters below whereby the binding rate kon was variated.
So the course in time for the free receptor, the monomeric receptor-NIP complex, the dimer and the active receptor is plotted:
kon = 0.2 :
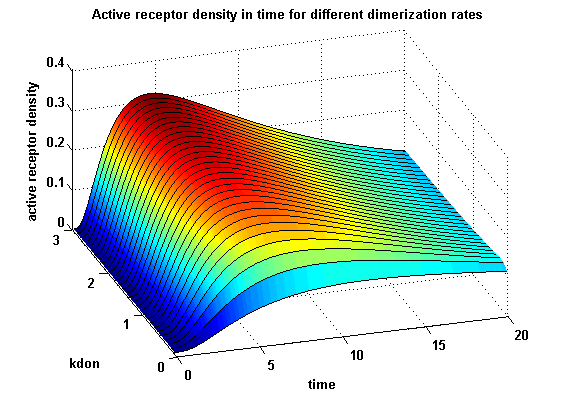
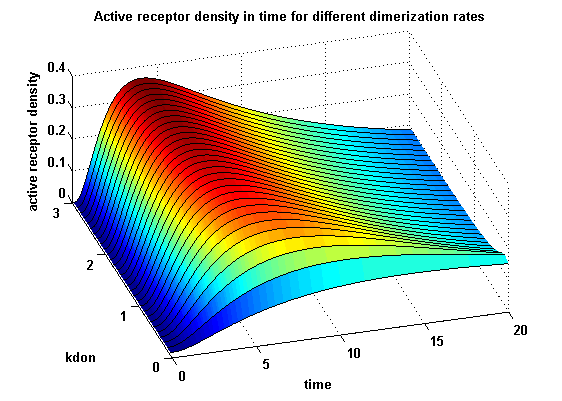
Receptor densities dependent on dimerization rate kdonApplying different kdon leads to the following result:
kdon = 0.3 :
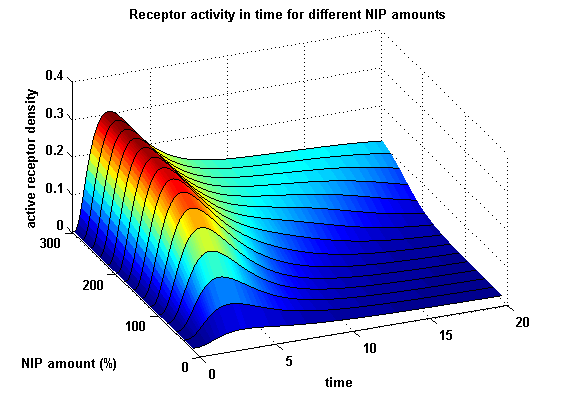
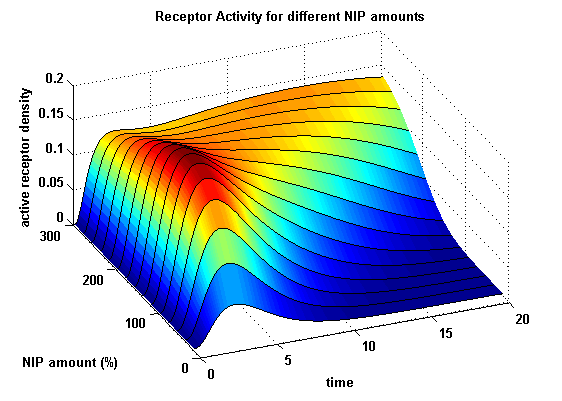
Receptor densities dependent on NIP amountThe use of different amounts of ligand is maybe the most important influence on the receptor activation. As the ligand is the stimulus in order to activate our system, it´s amount will determine strongly the activity of the receptor. So different amounts of NIP are used and a higher internalization rate ki is used aswell.
NIP = 0.1 :
Modular Synthetic Receptor System modelmatlab m-file Reaction kineticsODE derivationThe ODEs can be derived from the reaction kinetics again and are: Involved quantities and split protein activityThe ODEs are solved for a set of parameters and reveal the time courses of the quantities:
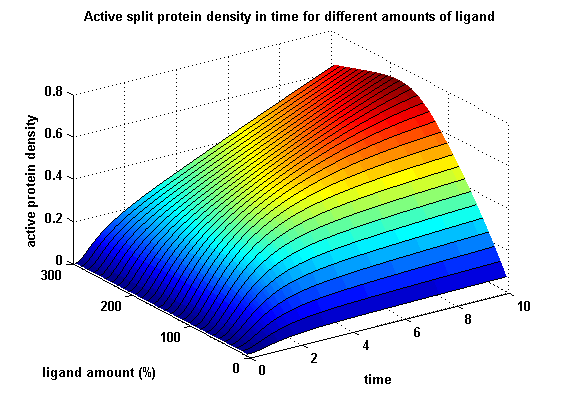
Active split protein density dependent on input ligand amountIn order to gain information about the split protein activity dependent on the input, the same parameters were used as above except the initial ligand parameter, which was variated.
Split protein activity with two different kinetic receptorsAs two different receptors are used, they can differ in the kinetics. Assuming that receptor R1 is binding the ligand better, so its binding rate is higher and its dissociating rate is lower than of receptor R2. Choosing not only a higher turnover rate s1 but also a higher dimerization and a lower dimer dissociating rate for receptor R1 and a lower initial free receptor density for R2, gives the following theoretical result:
Matlab m-files
|
 "
"