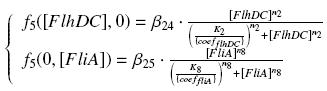Team:Paris/Modeling/f5

From 2008.igem.org

(Difference between revisions)
 
(18 intermediate revisions not shown)
Line 1: Line 1:
-
[[Image:f5DCA.png|thumb]]
+
{{Paris/Menu}}
 +
 
 +
{{Paris/Header|Method & Algorithm : ƒ5}}
 +
<center> = act_''pFliL'' </center>
 +
<br>
 +
 
 +
[[Image:f5DCA.png|thumb|Specific Plasmid Characterisation for &#131;5]]
 +
 
 +
According to the characterization plasmid (see right) and to our modeling, in the '''exponential phase of growth''', at the steady state,
 +
 
 +
we have ''' [''FlhDC'']<sub>''real''</sub> = {coef<sub>''flhDC''</sub>} &#131;1([aTc]<sub>i</sub>) '''
 +
and ''' [''FliA'']<sub>''real''</sub> = {coef<sub>''fliA''</sub>} &#131;2([arab]<sub>i</sub>) '''
 +
 
 +
but we use ''' [aTc]<sub>i</sub> = Inv_&#131;1( [''FlhDC''] ) '''
 +
and        ''' [arab]<sub>i</sub> = Inv_&#131;2( [''FliA''] ) '''
 +
 
 +
So, at steady-states,
 +
 
 +
[[Image:F5.jpg|center]]
 +
 
 +
we use this analytical expression to determine the parameters :
 +
 
 +
<div style="text-align: center">
 +
{{Paris/Toggle|Table of Values|Team:Paris/Modeling/More_f5_Table}}
 +
</div>
 +
 
 +
<div style="text-align: center">
 +
{{Paris/Toggle|Algorithm|Team:Paris/Modeling/More_FP_Algo}}
 +
</div>
 +
 
 +
Then, if we have time, we want to verify the expected relation
 +
 
 +
[[Image:SumpFliL.jpg|center]]
 +
 
 +
<br>
 +
 
 +
<center>
 +
[[Team:Paris/Modeling/Implementation| <Back - to "Implementation" ]]| <br>
 +
[[Team:Paris/Modeling/Protocol_Of_Characterization| <Back - to "Protocol Of Characterization" ]]|
 +
</center>

Latest revision as of 02:08, 30 October 2008

Method & Algorithm : ƒ5


= act_pFliL


Specific Plasmid Characterisation for ƒ5

According to the characterization plasmid (see right) and to our modeling, in the exponential phase of growth, at the steady state,

we have [FlhDC]real = {coefflhDC} ƒ1([aTc]i) and [FliA]real = {coeffliA} ƒ2([arab]i)

but we use [aTc]i = Inv_ƒ1( [FlhDC] ) and [arab]i = Inv_ƒ2( [FliA] )

So, at steady-states,

F5.jpg

we use this analytical expression to determine the parameters :

↓ Table of Values ↑


param signification unit value comments
(fluorescence) value of the observed fluorescence au need for 20 mesures with well choosen values of [aTc]i
and for 20 mesures with well choosen values of [arab]i
and 5x5 measures for the relation below?
conversion conversion ratio between
fluorescence and concentration
↓ gives ↓ 		nM.au-1 (1/79.429)
[GFP] GFP concentration at steady-state nM
γGFP dilution-degradation rate
of GFP(mut3b)
↓ gives ↓ 		min-1 0.0198 Time Cell Division : 35 min.
ƒ5 activity of
pFliL with RBS E0032 		nM.min-1



param signification
corresponding parameters in the equations 		unit value comments
β24 total transcription rate of
FlhDC><pFliL with RBS E0032
β24 		nM.min-1
(K2/{coeffliA}) activation constant of FlhDC><pFliL
K2 		nM
n2 complexation order of FlhDC><pFliL
n2 		no dimension
β25 total transcription rate of
FliA><pFliL with RBS E0032
β25 		nM.min-1
(K8/{coefflhDC}) activation constant of FliA><pFliL
K8 		nM
n8 complexation order of FliA><pFliL
n8 		no dimension
↓ Algorithm ↑


find_ƒP 

function optimal_parameters = find_FP(X_data, Y_data, initial_parameters)
% gives the 'best parameters' involved in f4, f5, f6, f7 or f8  
% with FlhDC = 0 or FliA = 0 by least-square optimisation
 
% X_data = vector of given values of [FliA]i or [FlhDC]i (experimentally
% controled)
% Y_data = vector of experimentally measured values f4, f5, f6, f7 or f8
% corresponding of the X_data
% initial_parameters = values of the parameters proposed by the literature
%                       or simply guessed
%                    = [beta, K -> (K)/(coef), n]
 
     function output = act_pProm(parameters, X_data)
         for k = 1:length(X_data)
                 output(k) = parameters(1)*hill(X_data(k), parameters(2), parameters(3));
         end
     end
 
options=optimset('LevenbergMarquardt','on','TolX',1e-10,'MaxFunEvals',1e10,'TolFun',1e-10,'MaxIter',1e4);
% options for the function lsqcurvefit
 
optimal_parameters = lsqcurvefit( @(parameters, X_data) act_pProm(parameters, X_data),...
     initial_parameters, X_data, Y_data, options );
% search for the fittest parameters, between 1/10 and 10 times the initial
% parameters
 
end

Then, if we have time, we want to verify the expected relation

SumpFliL.jpg


<Back - to "Implementation" |
<Back - to "Protocol Of Characterization" |

Retrieved from "http://2008.igem.org/Team:Paris/Modeling/f5"