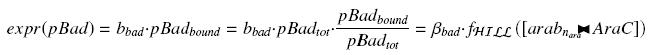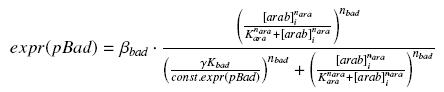Team:Paris/Modeling/f2

From 2008.igem.org

(Difference between revisions)
 
(6 intermediate revisions not shown)
Line 1: Line 1:
-
[[Image:f2.jpg|thumb]]
+
{{Paris/Menu}}
-
The experience would give us
+
{{Paris/Header|Method & Algorithm : ƒ2}}
 +
<center> = act_''pBad'' </center>
 +
<br>
 +
 
 +
[[Image:f2.jpg|thumb|Specific Plasmid Characterisation for &#131;2]]
 +
 
 +
According to the characterization plasmid (see right) and to our modeling, in the '''exponential phase of growth''', at the steady state, the experiment would give us
[[Image:f2expr.jpg|center]]
[[Image:f2expr.jpg|center]]
-
Thus, at steady-state and in the exponential phase of growth :
+
and at steady-state and in the exponential phase of growth, we expect :
[[Image:Exprpbad.jpg|center]]
[[Image:Exprpbad.jpg|center]]
-
{|border="1" style="text-align: center"
+
we use this analytical expression to determine the parameters :
-
|param
+
-
|signification
+
-
|unit
+
-
|value
+
-
|comments
+
-
|-
+
-
|[expr(pBad)]
+
-
|expression rate of <br> pBad '''with RBS E0032'''
+
-
|nM.min<sup>-1</sup>
+
-
|
+
-
|need for 20 measures with well choosen [arab]<sub>i</sub>
+
-
|-
+
-
|γ<sub>GFP</sub>
+
-
|dilution-degradation rate <br> of GFP(mut3b)
+
-
|min<sup>-1</sup>
+
-
|0.0198
+
-
|-
+
-
|[GFP]
+
-
|GFP concentration at steady-state
+
-
|nM
+
-
|
+
-
|need for 20 measures
+
-
|-
+
-
|(''fluorescence'')
+
-
|value of the observed fluorescence
+
-
|au
+
-
|
+
-
|need for 20 measures
+
-
|-
+
-
|''conversion''
+
-
|conversion ratio between <br> fluorescence and concentration
+
-
|nM.au<sup>-1</sup>
+
-
|(1/79.429)
+
-
|
+
-
|}
+
-
<br><br>
+
<div style="text-align: center">
 +
{{Paris/Toggle|Table of Values|Team:Paris/Modeling/More_f2_Table}}
 +
</div>
-
{|border="1" style="text-align: center"
+
<div style="text-align: center">
-
|param
+
{{Paris/Toggle|Algorithms|Team:Paris/Modeling/More_f2_Algo}}
-
|signification <br> corresponding parameters in the [[Team:Paris/Modeling/Oscillations#Resulting_Equations|equations]]
+
</div>
-
|unit
+
-
|value
+
-
|comments
+
-
|-
+
-
|β<sub>bad</sub>
+
-
|production rate of pBad '''with RBS E0032''' <br> not in the system
+
-
|nM.min<sup>-1</sup>
+
-
|
+
-
|
+
-
|-
+
-
|(&gamma; K<sub>bad</sub>/''const.expr(pBad)'')
+
-
|activation constant of pBad <br> not in the system
+
-
|nM
+
-
|
+
-
|
+
-
|-
+
-
|n<sub>bad</sub>
+
-
|complexation order of pBad<br> not in the system
+
-
|no dimension
+
-
|
+
-
|The literature [[Team:Paris/Modeling/Bibliography|[?]]] gives n<sub>bad</sub> =
+
-
|-
+
-
|K<sub>ara</sub>
+
-
|complexation constant Arabinose-AraC <br> not in the system
+
-
|nM
+
-
|
+
-
|The literature [[Team:Paris/Modeling/Bibliography|[?]]] gives K<sub>ara</sub> =
+
-
|-
+
-
|n<sub>ara</sub>
+
-
|complexation order Arabinose-AraC <br> not in the system
+
-
|no dimension
+
-
|
+
-
|The literature [[Team:Paris/Modeling/Bibliography|[?]]] gives n<sub>ara</sub> =
+
-
|}
+
That will give us directly &#131;2([arab])
That will give us directly &#131;2([arab])
 +
 +
<br>
 +
 +
<center>
 +
[[Team:Paris/Modeling/Implementation| <Back - to "Implementation" ]]| <br>
 +
[[Team:Paris/Modeling/Protocol_Of_Characterization| <Back - to "Protocol Of Characterization" ]]|
 +
</center>

Latest revision as of 02:05, 30 October 2008

Method & Algorithm : ƒ2


= act_pBad


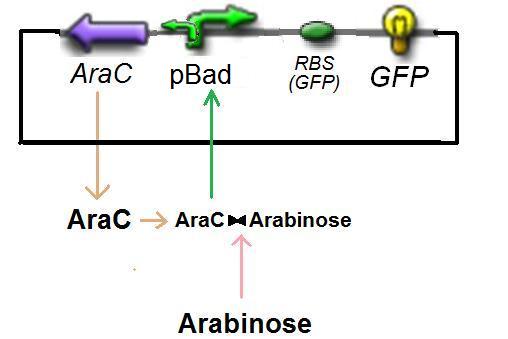Specific Plasmid Characterisation for ƒ2

According to the characterization plasmid (see right) and to our modeling, in the exponential phase of growth, at the steady state, the experiment would give us

F2expr.jpg

and at steady-state and in the exponential phase of growth, we expect :

Exprpbad.jpg

we use this analytical expression to determine the parameters :

↓ Table of Values ↑


param signification unit value comments
(fluorescence) value of the observed fluorescence au need for 20 measures with well choosen [arab]i
conversion conversion ratio between
fluorescence and concentration
↓ gives ↓ 		nM.au-1 (1/79.429)
[GFP] GFP concentration at steady-state nM
γGFP dilution-degradation rate
of GFP(mut3b)
↓ gives ↓ 		min-1 0.0198 Only Dilution
Time Cell Disvision : 35 min.
ƒ2 activity of
pBad with RBS E0032 		nM.min-1



param signification
corresponding parameters in the equations 		unit value comments
βbad total transcription rate of
pBad with RBS E0032
not in the Core System 		nM.min-1
(γ Kbad/const.expr(pBad)) activation constant of pBad
not in the Core System 		nM
nbad complexation order of pBad
not in the Core System 		no dimension The literature [?] gives nbad =
Kara complexation constant Arabinose><AraC
not in the Core System 		nM The literature [?] gives Kara =
nara complexation order Arabinose><AraC
not in the Core System 		no dimension The literature [?] gives nara =
↓ Algorithms ↑


find_ƒ2 

function optimal_parameters = find_f2(X_data, Y_data, initial_parameters)
% gives the 'best parameters' involved in f2 by least-square optimisation
 
% X_data = vector of given values of a [arab]i (experimentally
% controled)
% Y_data = vector of experimentally measured values f2 corresponding of
% the X_data
% initial_parameters = values of the parameters proposed by the literature
%                       or simply guessed
%                    = [betabad, (Kbad -> (gamma.Kbad)/(const.expr(pBad))), nbad, Kara, nara]
 
     function output = expr_pBad(parameters, X_data)
         for k = 1:length(X_data)
                 output(k) = parameters(1) * ( hill( ...
                     (hill(X_data(k), parameters(4), parameters(5))), parameters(2), parameters(3)) );
         end
     end
 
options=optimset('LevenbergMarquardt','on','TolX',1e-10,'MaxFunEvals',1e10,'TolFun',1e-10,'MaxIter',1e4);
% options for the function lsqcurvefit
 
optimal_parameters = lsqcurvefit( @(parameters, X_data) expr_pBad(parameters, X_data), ...
     initial_parameters, X_data, Y_data, 1/10*initial_parameters, 10*initial_parameters, options );
% search for the fittest parameters, between 1/10 and 10 times the initial
% parameters
end

Inv_ƒ2 

function quant_ara = Inv_f2(inducer_quantity)
% gives the quantity of [ara]i needed to get inducer_quantity of a protein
% throught a gene behind pBad
 
     function equa = F(x)
         equa = f2( x ) - inducer_quantity;
     end
 
options=optimset('LevenbergMarquardt','on','TolX',1e-10,'MaxFunEvals',1e10,'TolFun',1e-10,'MaxIter',1e4);
 
quant_ara = fsolve(F,1,options);
 
end

That will give us directly ƒ2([arab])


<Back - to "Implementation" |
<Back - to "Protocol Of Characterization" |

Retrieved from "http://2008.igem.org/Team:Paris/Modeling/f2"