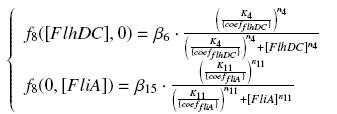Team:Paris/Modeling/f8

From 2008.igem.org

(Difference between revisions)
 
(3 intermediate revisions not shown)
Line 1: Line 1:
-
[[Image:f8DCA.png|thumb]]
+
{{Paris/Menu}}
-
We have [FlhDC] = {coef<sub>flhDC</sub>}''expr(pTet)'' = {coef<sub>flhDC</sub>} &#131;1([aTc]<sub>i</sub>)
+
{{Paris/Header|Method & Algorithm : &#131;8}}
 +
<center> = act_''pTet'' </center>
 +
<br>
-
and [FliA] = {coef<sub>FliA</sub>}''expr(pBad)'' = {coef<sub>FliA</sub>} &#131;2([arab]<sub>i</sub>)
+
[[Image:f6DCA.png|thumb|Specific Plasmid Characterisation for &#131;8]]
-
So, at steady-states,
+
According to the characterization plasmid (see right) and to our modeling, in the '''exponential phase of growth''', at the steady state,
-
[[Image:F8.jpg|center]]
+
we have ''' [''FlhDC'']<sub>''real''</sub> = {coef<sub>''flhDC''</sub>} &#131;1([aTc]<sub>i</sub>) '''
 +
and ''' [''FliA'']<sub>''real''</sub> = {coef<sub>''fliA''</sub>} &#131;2([arab]<sub>i</sub>) '''
 +
but we use ''' [aTc]<sub>i</sub> = Inv_&#131;1( [''FlhDC''] ) '''
 +
and        ''' [arab]<sub>i</sub> = Inv_&#131;2( [''FliA''] ) '''
-
{|border="1" style="text-align: center"
+
So, at steady-states,
-
|param
+
-
|signification
+
-
|unit
+
-
|value
+
-
|comments
+
-
|-
+
-
|[expr(pFlhDC)]
+
-
|expression rate of <br> pFlhDC '''with RBS E0032'''
+
-
|nM.min<sup>-1</sup>
+
-
|
+
-
|need for 20 mesures with well choosen values of [aTc]<sub>i</sub> <br> and for 20 mesures with well choosen values of [arab]<sub>i</sub> <br> and 5x5 measures for the relation below?
+
-
|-
+
-
|γ<sub>GFP</sub>
+
-
|dilution-degradation rate <br> of GFP(mut3b)
+
-
|min<sup>-1</sup>
+
-
|0.0198
+
-
|
+
-
|-
+
-
|[GFP]
+
-
|GFP concentration at steady-state
+
-
|nM
+
-
|
+
-
|need for 20 + 20 measures <br> and 5x5 measures for the relation below?
+
-
|-
+
-
|(''fluorescence'')
+
-
|value of the observed fluorescence
+
-
|au
+
-
|
+
-
|need for 20 + 20 measures <br> and 5x5 measures for the relation below?
+
-
|-
+
-
|''conversion''
+
-
|conversion ratio between <br> fluorescence and concentration
+
-
|nM.au<sup>-1</sup>
+
-
|(1/79.429)
+
-
|
+
-
|}
+
-
<br><br>
+
[[Image:F8.jpg|center]]
-
{|border="1" style="text-align: center"
+
we use this analytical expression to determine the parameters :
-
|param
+
-
|signification <br> corresponding parameters in the [[Team:Paris/Modeling/Oscillations#Resulting_Equations|equations]]
+
-
|unit
+
-
|value
+
-
|comments
+
-
|-
+
-
|β<sub>6</sub>
+
-
|production rate of FlhDC-pFlhB '''with RBS E0032''' <br> β<sub>6</sub>
+
-
|nM.min<sup>-1</sup>
+
-
|
+
-
|
+
-
|-
+
-
|(K<sub>4</sub>/{coef<sub>fliA</sub>})
+
-
|activation constant of FlhDC-pFlhB <br> K<sub>4</sub>
+
-
|nM
+
-
|
+
-
|
+
-
|-
+
-
|n<sub>4</sub>
+
-
|complexation order of FlhDC-pFlhB <br> n<sub>4</sub>
+
-
|no dimension
+
-
|
+
-
|
+
-
|-
+
-
|β<sub>15</sub>
+
-
|production rate of FliA-pFlhB '''with RBS E0032''' <br> β<sub>15</sub>
+
-
|nM.min<sup>-1</sup>
+
-
|
+
-
|
+
-
|-
+
-
|(K<sub>11</sub>/{coef<sub>omp</sub>})
+
-
|activation constant of FliA-pFlhB <br> K<sub>11</sub>
+
-
|nM
+
-
|
+
-
|
+
-
|-
+
-
|n<sub>11</sub>
+
-
|complexation order of FliA-pFlhB <br> n<sub>11</sub>
+
-
|no dimension
+
-
|
+
-
|
+
-
|}
+
-
<br><br>
+
<div style="text-align: center">
 +
{{Paris/Toggle|Table of Values|Team:Paris/Modeling/More_f8_Table}}
 +
</div>
 +
 
 +
<div style="text-align: center">
 +
{{Paris/Toggle|Algorithm|Team:Paris/Modeling/More_FP_Algo}}
 +
</div>
Then, if we have time, we want to verify the expected relation
Then, if we have time, we want to verify the expected relation
[[Image:SumpFlhB.jpg|center]]
[[Image:SumpFlhB.jpg|center]]
 +
 +
<br>
 +
 +
<center>
 +
[[Team:Paris/Modeling/Implementation| <Back - to "Implementation" ]]| <br>
 +
[[Team:Paris/Modeling/Protocol_Of_Characterization| <Back - to "Protocol Of Characterization" ]]|
 +
</center>

Latest revision as of 02:11, 30 October 2008

Method & Algorithm : ƒ8


= act_pTet


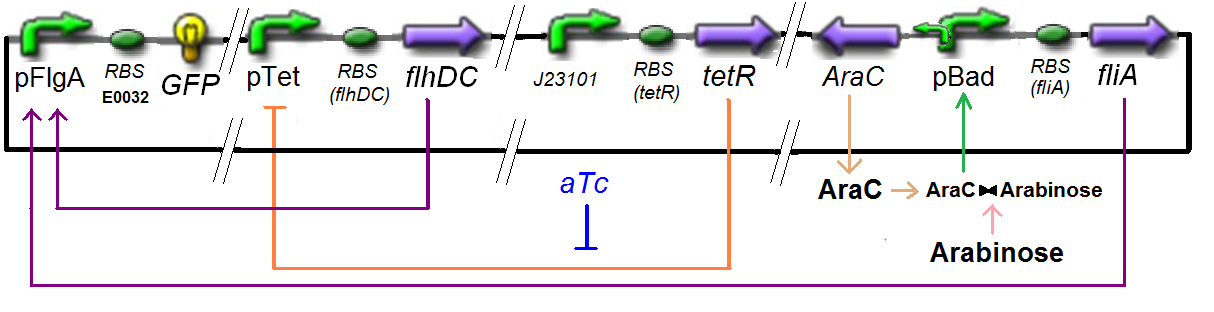Specific Plasmid Characterisation for ƒ8

According to the characterization plasmid (see right) and to our modeling, in the exponential phase of growth, at the steady state,

we have [FlhDC]real = {coefflhDC} ƒ1([aTc]i) and [FliA]real = {coeffliA} ƒ2([arab]i)

but we use [aTc]i = Inv_ƒ1( [FlhDC] ) and [arab]i = Inv_ƒ2( [FliA] )

So, at steady-states,

F8.jpg

we use this analytical expression to determine the parameters :

↓ Table of Values ↑


param signification unit value comments
(fluorescence) value of the observed fluorescence au need for 20 mesures with well choosen values of [aTc]i
and for 20 mesures with well choosen values of [arab]i
and 5x5 measures for the relation below?
conversion conversion ratio between
fluorescence and concentration
↓ gives ↓ 		nM.au-1 (1/79.429)
[GFP] GFP concentration at steady-state nM
γGFP dilution-degradation rate
of GFP(mut3b)
↓ gives ↓ 		min-1 0.0198 Time Cell Division : 35 min.
ƒ8 activity of
pFlhB with RBS E0032 		nM.min-1



param signification
corresponding parameters in the equations 		unit value comments
β30 total transcription rate of
FlhDC><pFlhB with RBS E0032
β30 		nM.min-1
(K5/{coeffliA}) activation constant of FlhDC><pFlhB
K5 		nM
n5 complexation order of FlhDC><pFlhB
n5 		no dimension
β31 total transcription rate of
FlhDC><pFlhB with RBS E0032
β31 		nM.min-1
(K11/{coefflhDC}) activation constant of FlhDC><pFlhB
K11 		nM
n11 complexation order of FlhDC><pFlhB
n11 		no dimension
↓ Algorithm ↑


find_ƒP 

function optimal_parameters = find_FP(X_data, Y_data, initial_parameters)
% gives the 'best parameters' involved in f4, f5, f6, f7 or f8  
% with FlhDC = 0 or FliA = 0 by least-square optimisation
 
% X_data = vector of given values of [FliA]i or [FlhDC]i (experimentally
% controled)
% Y_data = vector of experimentally measured values f4, f5, f6, f7 or f8
% corresponding of the X_data
% initial_parameters = values of the parameters proposed by the literature
%                       or simply guessed
%                    = [beta, K -> (K)/(coef), n]
 
     function output = act_pProm(parameters, X_data)
         for k = 1:length(X_data)
                 output(k) = parameters(1)*hill(X_data(k), parameters(2), parameters(3));
         end
     end
 
options=optimset('LevenbergMarquardt','on','TolX',1e-10,'MaxFunEvals',1e10,'TolFun',1e-10,'MaxIter',1e4);
% options for the function lsqcurvefit
 
optimal_parameters = lsqcurvefit( @(parameters, X_data) act_pProm(parameters, X_data),...
     initial_parameters, X_data, Y_data, options );
% search for the fittest parameters, between 1/10 and 10 times the initial
% parameters
 
end

Then, if we have time, we want to verify the expected relation

SumpFlhB.jpg


<Back - to "Implementation" |
<Back - to "Protocol Of Characterization" |

Retrieved from "http://2008.igem.org/Team:Paris/Modeling/f8"