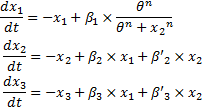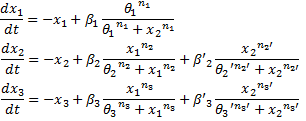|
|
| (47 intermediate revisions not shown) |
| Line 1: |
Line 1: |
| | {{Paris/Menu}} | | {{Paris/Menu}} |
| - | <br>
| + | {{Paris/Header|Model Construction}} |
| - | <center><html><div style="color:#275D96; font-size:2em;">Model construction</div></html></center>
| + | {{Paris/Section_contents_analysis}} |
| - | <br>
| + | |
| | | | |
| - | = Introduction = biblio | + | = Introduction = |
| - | A FAIRE
| + | |
| - | We wished to build a model that could be used to help us design our biological system. We shall hereby describe the asumptions we made
| + | |
| | | | |
| - | = Classical model and time resetting = | + | * This approach is mainly based on a bibliographical work. We found essential to choose only parameters that could be found in literature so as to get quickly a first idea of the way our system could behave. |
| - | * Classically we use the following equation to model gene interactions (see for example in [[Team:Paris/Modeling/BOB#Bibliography|[5]]]) : | + | * In this section, we will present the model we chose to describe the evolution of our system's concentrations. |
| | + | |
| | + | = Classical model and temporal rescaling = |
| | + | * Classically we use the following equation to model gene interactions (see for example in [[Team:Paris/Modeling/BOB#Bibliography|[1]]]) : |
| | <br> | | <br> |
| | [[Image:Classical_equation.jpg|center]] | | [[Image:Classical_equation.jpg|center]] |
| Line 15: |
Line 15: |
| | where [Y] denotes the concentration of Y protein and γ its degradation rate (which unit is time<sup>-1</sup>). | | where [Y] denotes the concentration of Y protein and γ its degradation rate (which unit is time<sup>-1</sup>). |
| | <br> | | <br> |
| - | *Then, we wanted to have a proper time scale. We then set the degradation rates, γ ,to 1. It is important to note that this degradation rate represents both the influence of the degradation and dilution. We assume that the degradation can be neglected compared to the dilution caused by the cell growth. Then we have: | + | * This system has been extensively studied in [[Team:Paris/Modeling/BOB#Bibliography|S.Kalir and U. Alon article]]. A lot of experimental data obtained in similar experimental conditions are available. Moreover models have been built for the FIFO part of the system so that '''we were able to use directly their experimentally determined parameters'''. When we did not find relevant information, we chose a classical Hill function. |
| | + | |
| | + | * To decrease the number of parameters we normalized every protein concentration, so that their value would range between 0 and 1. Moreover, we found it convenient because it enabled us to compare the respective influences of these concentrations. |
| | + | |
| | + | * Furthermore, it is important to note that this degradation rate represents both the influence of the degradation and dilution. We assume that the degradation can be neglected compared to the dilution caused by the cell growth. Thus, '''every degradation rates are assumed equal'''. We kept the designation “degradation rate” for convenience, so as not to mix up with the dilution that might occur elsewhere. |
| | + | |
| | + | * We therefore wanted to have a proper time scale. By setting the degradation rates, γ ,to 1, a time unit corresponds to . Since we can know easily the value of the real half-time, we may know the real timescale out of our computations. Then we have: |
| | <br> | | <br> |
| | [[Image:Gamma_Expression.jpg|center]] | | [[Image:Gamma_Expression.jpg|center]] |
| | <br> | | <br> |
| - | *Since we can know easily the value of the real half-time, we may know the real timescale out of our computations. We kept the designation “degradation rate” for convenience, so as not to mix up with the dilution that occurs with the HSL in the synchronisation step.
| |
| - |
| |
| - |
| |
| - |
| |
| | | | |
| | + | * Finally, the key problem with a dynamic system consists in the fact that adding a new equation gives a more detailed idea of the overall process, but one looses meaning by doing so since new undefined parameters appear. Hence, it becomes hard to link those parameters with a biological meaning and reality. In that respect, we chose not to introduce the mRNA state between transcription and translation in our model. We presented things as if a protein would act directly upon the following. |
| | | | |
| | = Conclusion = | | = Conclusion = |
| - | This finally gave the following equations :
| + | We finally obtained the following equations : |
| | | | |
| - | [[Image:eqn_flhDC|center]]
| |
| | [[Image:FliA_dynamics.jpg|center]] | | [[Image:FliA_dynamics.jpg|center]] |
| - | [[Image:CFP.jpg|center]] | + | [[Image:CFP.jpg|center]] |
| | [[Image:YFP.jpg|center]] | | [[Image:YFP.jpg|center]] |
| - | [[Image:RFP.jpg|center]] | + | [[Image:eqn_EnvZ-RFP.jpg|center]] |
| | + | [[Image:eqn_flhDC.jpg|center]] |
| | + | |
| | + | |
| | + | and the following parameters : |
| | + | |
| | + | <center> |
| | + | {| |
| | + | |- style="background: #649CD7;" |
| | + | ! colspan="6" style="background: #649CD7;" | Parameter Table |
| | + | |- style="background: #649CD7; text-align: center;" |
| | + | | Parameter |
| | + | | Meaning |
| | + | | Original Value |
| | + | | Normalized Value |
| | + | | Unit |
| | + | | Source |
| | + | |
| | + | |
| | + | |- style="background: #dddddd;" |
| | + | | style="background: #D4E2EF;"|γ |
| | + | | Degradation rate |
| | + | | 0.0198 |
| | + | | 1 |
| | + | | min<sup>-1</sup> |
| | + | | [[Team:Paris/Modeling/BOB#Remarks|wet-lab]] |
| | + | |- style="background: #dddddd;" |
| | + | | style="background: #D4E2EF;"|β<sub>FliA</sub> |
| | + | | FlhDC activation coefficient |
| | + | | 50 |
| | + | | 0.1429 |
| | + | | min<sup>-1</sup> |
| | + | | [[Team:Paris/Modeling/BOB#Bibliography|[1]]] |
| | + | |- style="background: #dddddd;" |
| | + | | style="background: #D4E2EF;"|β'<sub>FliA</sub> |
| | + | | FliA activation coefficient |
| | + | | 300 |
| | + | | 0.8571 |
| | + | | min<sup>-1</sup> |
| | + | | [[Team:Paris/Modeling/BOB#Bibliography|[1]]] |
| | + | |- style="background: #dddddd;" |
| | + | | style="background: #D4E2EF;"|β<sub>CFP</sub> |
| | + | | FlhDC activation coefficient |
| | + | | 1200 |
| | + | | 0.8276 |
| | + | | min<sup>-1</sup> |
| | + | | [[Team:Paris/Modeling/BOB#Bibliography|[1]]] |
| | + | |- style="background: #dddddd;" |
| | + | | style="background: #D4E2EF;"|β'<sub>CFP</sub> |
| | + | | FliA activation coefficient |
| | + | | 250 |
| | + | | 0.1724 |
| | + | | min<sup>-1</sup> |
| | + | | [[Team:Paris/Modeling/BOB#Bibliography|[1]]] |
| | + | |- style="background: #dddddd;" |
| | + | | style="background: #D4E2EF;" |β<sub>YFP</sub> |
| | + | | FlhDC activation coefficient |
| | + | | 150 |
| | + | | 0.3333 |
| | + | | min<sup>-1</sup> |
| | + | | [[Team:Paris/Modeling/BOB#Bibliography|[1]]] |
| | + | |- style="background: #dddddd;" |
| | + | | style="background: #D4E2EF;" |β'<sub>YFP</sub> |
| | + | | FliA activation coefficient |
| | + | | 300 |
| | + | | 0.6667 |
| | + | | min<sup>-1</sup> |
| | + | | [[Team:Paris/Modeling/BOB#Bibliography|[1]]] |
| | + | |- style="background: #dddddd;" |
| | + | | style="background: #D4E2EF;" |β<sub>EnvZ-RFP</sub> |
| | + | | FlhDC activation coefficient |
| | + | | 100 |
| | + | | 0.2222 |
| | + | | min<sup>-1</sup> |
| | + | | [[Team:Paris/Modeling/BOB#Bibliography|[1]]] |
| | + | |- style="background: #dddddd;" |
| | + | | style="background: #D4E2EF;" |β'<sub>EnvZ-RFP</sub> |
| | + | | FliA activation coefficient |
| | + | | 350 |
| | + | | 0.7778 |
| | + | | min<sup>-1</sup> |
| | + | | [[Team:Paris/Modeling/BOB#Bibliography|[1]]] |
| | + | |- style="background: #dddddd;" |
| | + | | style="background: #D4E2EF;" |β<sub>FlhDC</sub> |
| | + | | Maximum production rate |
| | + | | |
| | + | | 1 |
| | + | | min<sup>-1</sup> |
| | + | | [[Team:Paris/Modeling/BOB#Remarks|∅]] |
| | + | |- style="background: #dddddd;" |
| | + | | style="background: #D4E2EF;" |n<sub>envZ</sub> |
| | + | | Hill coefficient |
| | + | | |
| | + | | 4 |
| | + | | ¤ |
| | + | | [[Team:Paris/Modeling/BOB#Bibliography|∅]] |
| | + | |- style="background: #dddddd;" |
| | + | | style="background: #D4E2EF;" |θ<sub>envZ</sub> |
| | + | | Hill characteristic concentration |
| | + | | |
| | + | | 0.5 |
| | + | | [[Team:Paris/Modeling/BOB#Remarks|c.u]] |
| | + | | [[Team:Paris/Modeling/BOB#Bibliography|∅]] |
| | + | |}</center> |
| | | | |
| - | = Liens =
| + | Now you have had a good overlook of our model, go see a more detailed justification where our normalization choices are thouroughly explained : |
| | + | {{Paris/Toggle|Detailed justification|Team:Paris/Network_analysis_and_design/Core_system/Model_construction/Detailed_justification}} |
| | | | |
| | + | Moreover, in order to take into account the fact that data are obtained form 'real' experiments (number of parameters, length of data set) we hereby propose a '''criteria to legitimate the chosen model depending on the experimental conditions''', in comparison with a more general model (Hill functions). |
| | | | |
| - | <center>[[Team:Paris/Network_analysis_and_design/Core_system|Back to the overall presentation of our Core System]]</center>
| + | {{Paris/Toggle|Akaike Criteria|Team:Paris/Network_analysis_and_design/Core_system/Model_construction/Akaike}} |
| - | <center>[[Team:Paris/Network_analysis_and_design/Core_system/Model_construction|Top of the page]]</center>
| + | |
| | | | |
| - | <center>[[Team:Paris/Network_analysis_and_design/Core_system/Model_construction/Detailed_justification|Have a look at our detailed justification!]] [[Team:Paris/Network_analysis_and_design/Core_system/Model_construction/Akaike|Have a look at our Akaike criteria!]]</center>
| + | {{Paris/Navig|Team:Paris/Analysis}} |
| | | | |
| | = Bibliography = | | = Bibliography = |
| | * [1] Shiraz Kalir, Uri Alon. ''Using quantitative blueprint to reprogram the dynamics of the flagella network.'' Cell, June 11, 2004, Vol.117, 713-720. | | * [1] Shiraz Kalir, Uri Alon. ''Using quantitative blueprint to reprogram the dynamics of the flagella network.'' Cell, June 11, 2004, Vol.117, 713-720. |
|
Model Construction
Introduction
- This approach is mainly based on a bibliographical work. We found essential to choose only parameters that could be found in literature so as to get quickly a first idea of the way our system could behave.
- In this section, we will present the model we chose to describe the evolution of our system's concentrations.
Classical model and temporal rescaling
- Classically we use the following equation to model gene interactions (see for example in [1]) :
where [Y] denotes the concentration of Y protein and γ its degradation rate (which unit is time-1).
- This system has been extensively studied in S.Kalir and U. Alon article. A lot of experimental data obtained in similar experimental conditions are available. Moreover models have been built for the FIFO part of the system so that we were able to use directly their experimentally determined parameters. When we did not find relevant information, we chose a classical Hill function.
- To decrease the number of parameters we normalized every protein concentration, so that their value would range between 0 and 1. Moreover, we found it convenient because it enabled us to compare the respective influences of these concentrations.
- Furthermore, it is important to note that this degradation rate represents both the influence of the degradation and dilution. We assume that the degradation can be neglected compared to the dilution caused by the cell growth. Thus, every degradation rates are assumed equal. We kept the designation “degradation rate” for convenience, so as not to mix up with the dilution that might occur elsewhere.
- We therefore wanted to have a proper time scale. By setting the degradation rates, γ ,to 1, a time unit corresponds to . Since we can know easily the value of the real half-time, we may know the real timescale out of our computations. Then we have:
- Finally, the key problem with a dynamic system consists in the fact that adding a new equation gives a more detailed idea of the overall process, but one looses meaning by doing so since new undefined parameters appear. Hence, it becomes hard to link those parameters with a biological meaning and reality. In that respect, we chose not to introduce the mRNA state between transcription and translation in our model. We presented things as if a protein would act directly upon the following.
Conclusion
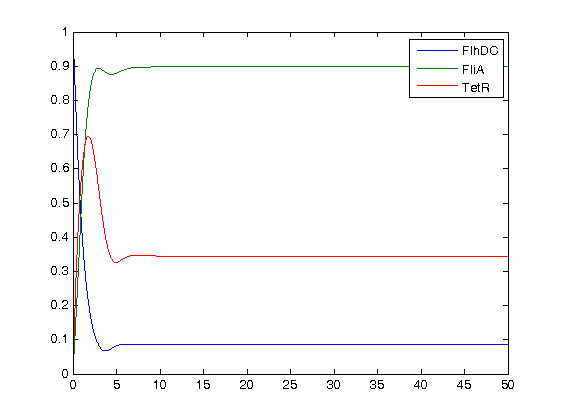
We finally obtained the following equations :
and the following parameters :
| Parameter Table
|
| Parameter
| Meaning
| Original Value
| Normalized Value
| Unit
| Source
|
| γ
| Degradation rate
| 0.0198
| 1
| min-1
| wet-lab
|
| βFliA
| FlhDC activation coefficient
| 50
| 0.1429
| min-1
| [1]
|
| β'FliA
| FliA activation coefficient
| 300
| 0.8571
| min-1
| [1]
|
| βCFP
| FlhDC activation coefficient
| 1200
| 0.8276
| min-1
| [1]
|
| β'CFP
| FliA activation coefficient
| 250
| 0.1724
| min-1
| [1]
|
| βYFP
| FlhDC activation coefficient
| 150
| 0.3333
| min-1
| [1]
|
| β'YFP
| FliA activation coefficient
| 300
| 0.6667
| min-1
| [1]
|
| βEnvZ-RFP
| FlhDC activation coefficient
| 100
| 0.2222
| min-1
| [1]
|
| β'EnvZ-RFP
| FliA activation coefficient
| 350
| 0.7778
| min-1
| [1]
|
| βFlhDC
| Maximum production rate
|
| 1
| min-1
| ∅
|
| nenvZ
| Hill coefficient
|
| 4
| ¤
| ∅
|
| θenvZ
| Hill characteristic concentration
|
| 0.5
| c.u
| ∅
|
Now you have had a good overlook of our model, go see a more detailed justification where our normalization choices are thouroughly explained :
↓ Detailed justification ↑
|
We shall present here a more detailed presentation of the choice we made as far as our model is concerned
Sum effect and linear modelling
- The flagella gene network has been thoroughly studied in [1]. We used two major results presented in this study. Firstly, Shiraz Kalir and Uri Alon came up with the fact that the promoters of class 2 genes, among which fliL, flgA and flhB, behaved like SUM-gate functions with flhDC and fliA inputs. Secondly, their experiments proved that these influences could be considered as linear. Thus the following model:
β and β’ represent the relative influence of flhDC and fliA respectively, the units of β and β’ being time-1.
- Furthermore, they came up with numerical values of β and β’ for each gene, which fitted quite well to their experiments. Since our experimental conditions are similar to those described in the article, we decided that we could use those values as well in our model.
- Thus the resulting equations
Hill function
When we had no relevant information, we decided to model the promoter activity by a Hill function. This was the case for the effect of envZ over FlhDC :
Thus the dynamic equation for [FlhDC] :
As for the parameters, we decided to chose biologically feasible values, that is nEnvZ=4 and θEnvZ=0.5.
Normalization
FliA, CFP, YFP, EnvZ-RFP
We kept the β and β’ values found by S. Kalir and U. Alon, since they showed the relative influence of flhDC and fliA. To have the same order of magnitude between each specie, we normalized those parameters between 0 and 1 as following. We reasoned independently for each equation, wishing to set the equilibrium values of the concentration to 1 given input values of 1. With the values taken from S. Kalir and U. Alon, this gave:
- In fact, if we take CFP for example:
The maximum of [CFP] is reached when [fliA] = 1 and [flhDC] = 1 ; when we solve with these condidtions, we obtain :
Then setting the equilibrium value of [CFP] to 1 corresponds to setting
- The analysis of fliA is different, but not the result:
With an input of flhDC equal to 1, the solution of the differential equation is:
And the condition on the equilibrium imposes
- To conclude, we see that we always get the same condition:
- Finally, since we had imposed γ=1 we resulted with β+β'=1.
FlhDC
- Likewise the previous analysis, we set γFlhDC to 1. Then, since FlhDC is fully expressed when envZ is not, we see that when solving under this conditions, we get
hence the need to set
- This is highly interesting since normalization implies that βFlhDC=1 , so that we do not need to find a value for βFlhDC.
- Furthermore, since [EnvZ] has been normalized, we have to do so for θEnvZ as well, since its role is to stand as a reference concentration for EnvZ. Therefore, we have to normalize it in the same way we did for [EnvZ]:
we had
which means we have to impose :
Time rescaling
We evaluated in the wet lab the half life time for our cells, and then calculated the degradation constants using :
The value for half-life time we found and used is 35min. Setting γ to one, gave us the time rescaling factor (0.0198).
Parameters table
| Parameter Table
|
| Parameter
| Meaning
| Original Value
| Normalized Value
| Unit
| Source
|
| γ
| Degradation rate
| 0.0198
| 1
| min-1
| wet-lab
|
| βFliA
| FlhDC activation coefficient
| 50
| 0.1429
| min-1
| [1]
|
| β'FliA
| FliA activation coefficient
| 300
| 0.8571
| min-1
| [1]
|
| βCFP
| FlhDC activation coefficient
| 1200
| 0.8276
| min-1
| [1]
|
| β'CFP
| FliA activation coefficient
| 250
| 0.1724
| min-1
| [1]
|
| βYFP
| FlhDC activation coefficient
| 150
| 0.3333
| min-1
| [1]
|
| β'YFP
| FliA activation coefficient
| 300
| 0.6667
| min-1
| [1]
|
| βEnvZ-RFP
| FlhDC activation coefficient
| 100
| 0.2222
| min-1
| [1]
|
| β'EnvZ-RFP
| FliA activation coefficient
| 350
| 0.7778
| min-1
| [1]
|
| βFlhDC
| Maximum production rate
|
| 1
| min-1
| ∅
|
| nenvZ
| Hill coefficient
|
| 4
| ¤
| ∅
|
| θenvZ
| Hill characteristic concentration
|
| 0.5
| c.u
| ∅
|
c.u. being an arbitrary concentration unit.
|
Moreover, in order to take into account the fact that data are obtained form 'real' experiments (number of parameters, length of data set) we hereby propose a criteria to legitimate the chosen model depending on the experimental conditions, in comparison with a more general model (Hill functions).
↓ Akaike Criteria ↑
|
Using mathematical criteria to discriminate between model
- When building a model, it is of the utmost importance to present a justification of the choice made along the transposition process from biological reality to mathematical representation. The aim of this section is to introduce a mathematical justification of the choice we made since it seems remote from biological reality. The criterion presented below are to help choosing the most relevant model given the experimental constraints.
Short introduction to the criteria
- Using linear equations in a biological system might seem awkward. However, we did prove the relevance of this approach. We have been looking for a criterion that would penalize a system that had many parameters, but that would also penalize a system which quadratic error would be too important while fitting experimental values. The goal here is to decide whether, assuming that the experimental data looks like a model based on Hill functions, the linear part of the model is obsolete or not.
- Several criteria taken from the information theory met our demands quite well :
Akaike criterion :
Hurvich and Tsai criterion :
Schwarz criterion :
where n denotes the number of experimental values, k the number of parameters and RSS the residual sum of squares.
The best fitting model is the one for which those criteria are minimized.
- It is remarkable that Akaike criterion and Hurvich and Tsai criterion are alike. AICc is therefore used for small sample size, but converges to AIC as n gets large. Since we will work with 20 points for each experiment, it seemed relevant to present both criteria. In addition, Schwarz criterion is meant to be more penalizing.
Experiment
- As an experiment, we compared the two models presented below :
System#1 : using the linear equations found in bibliography :
System#2 : using classical Hill functions :
- We made a set of data out of a noised Hill function. In fact, our data set was made by using the same equations as System#2, but we introduced a normal noise for each point. Thus, System#1 is penalized because its RSS will be greater than that of System#2. Nevertheless, System#2 will be more penalized by its number of parameters.
- With Matlab, we run a fitting simulation for each system, and we obtained the RSS. We then evaluated the different criteria for both models. We chose to act as if the length of our experimental data set was 20 (which is what we would have gotten in reality). The results are presented below.
| Comparison of the systems for n=20
|
| Criteria
| System#1
| System#2
|
| AIC
| 26.7654
| 32.0035
|
| AICc
| 38.7654
| 168.0035
|
| BIC
| 22.9435
| 24.3596
|
| Comparison of the systems for n=100
|
| Criteria
| System#1
| System#2
|
| AIC
| 169.5495
| 32.1150
|
| AICc
| 171.1147
| 38.5912
|
| BIC
| 172.0100
| 37.0360
|
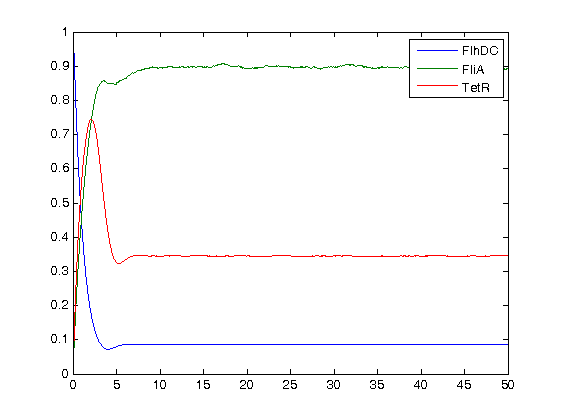
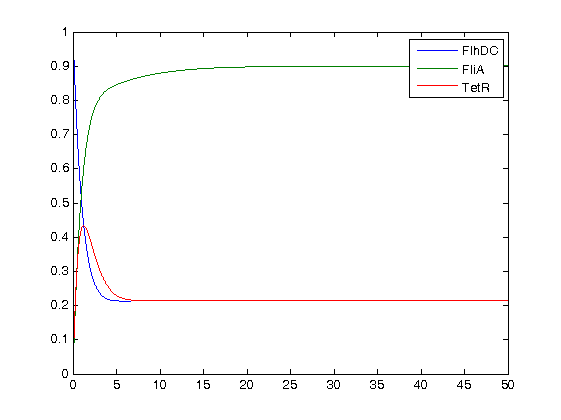
- Finally, we ran the simulation plots obtained for the parameters that best fitted. Here are the results proving that no numerical errors were to be seen :
Then, we see that the model that uses linear equations does not fit that well, but under certain conditions it is not so bad. Indeed, if the data set is short, this kind model is a relevant model since it eases the understanding of the dynamics.
- Consequently, what have we proved? These results show that:
- We may see that, as predicted, System#2 is not penalized anymore for greater values of n, although System#1 is. Consequently, we may adapt our system knowing the length of the data set we are going to obtain experimentally.
- However, since for a larger set of data System#2 minimizes the criteria, these criteria cannot decide whether a model is "better" than another one, since those criteria are arbitrary. Yet, they may help us find a better compromise between simplification and accuracy.
- Consequently, these criteria corroborate our choice of a linear model.
A fundamental tool?
Why can we introduce this seemingly awkward criteria as being a fundamental tool? This precise criteria enables the mathematician to adapt its model. In fact, in that respect, conducting this analysis over his model gives tangible arguments to the mathematician to use such and such model. Indeed, in our precise case, if we have about 20 experimental points to fit, the linear approach is sufficient. However, if we get 50 points, it becomes inadequate compared to a model with Hill functions. We believe that this kind of criteria is an essential tool, that might help the model maker to comprehend and control the assumptions he made while creating his model.
- We mostly used the definition of the criteria given in :
[http://www.liebertonline.com/doi/pdf/10.1089/rej.2006.9.324 K. Kikkawa.Statistical issue of regression analysis on development of an age predictive equation. Rejuvenation research, Volume 9, n°2, 2006.]
|


Bibliography
- [1] Shiraz Kalir, Uri Alon. Using quantitative blueprint to reprogram the dynamics of the flagella network. Cell, June 11, 2004, Vol.117, 713-720.
|
 "
"