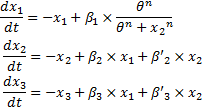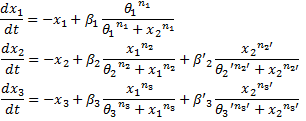Team:Paris/Analysis/Construction
From 2008.igem.org
(→Conclusion) |
|||
| (23 intermediate revisions not shown) | |||
| Line 1: | Line 1: | ||
{{Paris/Menu}} | {{Paris/Menu}} | ||
| - | + | {{Paris/Header|Model Construction}} | |
| - | + | {{Paris/Section_contents_analysis}} | |
| - | + | ||
= Introduction = | = Introduction = | ||
| - | * This | + | * This approach is mainly based on a bibliographical work. We found essential to choose only parameters that could be found in literature so as to get quickly a first idea of the way our system could behave. |
* In this section, we will present the model we chose to describe the evolution of our system's concentrations. | * In this section, we will present the model we chose to describe the evolution of our system's concentrations. | ||
| Line 16: | Line 15: | ||
where [Y] denotes the concentration of Y protein and γ its degradation rate (which unit is time<sup>-1</sup>). | where [Y] denotes the concentration of Y protein and γ its degradation rate (which unit is time<sup>-1</sup>). | ||
<br> | <br> | ||
| - | * | + | * This system has been extensively studied in [[Team:Paris/Modeling/BOB#Bibliography|S.Kalir and U. Alon article]]. A lot of experimental data obtained in similar experimental conditions are available. Moreover models have been built for the FIFO part of the system so that '''we were able to use directly their experimentally determined parameters'''. When we did not find relevant information, we chose a classical Hill function. |
| - | * | + | * To decrease the number of parameters we normalized every protein concentration, so that their value would range between 0 and 1. Moreover, we found it convenient because it enabled us to compare the respective influences of these concentrations. |
| - | * Furthermore, it is important to note that this degradation rate represents both the influence of the degradation and dilution. We assume that the degradation can be neglected compared to the dilution caused by the cell growth. Thus, every degradation rates are equal. We kept the designation “degradation rate” for convenience, so as not to mix up with the dilution that might occur elsewhere. | + | * Furthermore, it is important to note that this degradation rate represents both the influence of the degradation and dilution. We assume that the degradation can be neglected compared to the dilution caused by the cell growth. Thus, '''every degradation rates are assumed equal'''. We kept the designation “degradation rate” for convenience, so as not to mix up with the dilution that might occur elsewhere. |
| - | * We therefore wanted to have a proper time scale. | + | * We therefore wanted to have a proper time scale. By setting the degradation rates, γ ,to 1, a time unit corresponds to . Since we can know easily the value of the real half-time, we may know the real timescale out of our computations. Then we have: |
<br> | <br> | ||
[[Image:Gamma_Expression.jpg|center]] | [[Image:Gamma_Expression.jpg|center]] | ||
<br> | <br> | ||
| - | * Finally, the key problem with a dynamic system consists in the fact that adding a new equation gives a more detailed idea of the overall process, but one looses meaning by doing so since new undefined parameters appear. Hence, it becomes hard to link those parameters with a biological meaning and reality. In that respect, we chose not to introduce the mRNA state between transcription and translation in our model. We presented things as if a protein would act directly upon the following. | + | * Finally, the key problem with a dynamic system consists in the fact that adding a new equation gives a more detailed idea of the overall process, but one looses meaning by doing so since new undefined parameters appear. Hence, it becomes hard to link those parameters with a biological meaning and reality. In that respect, we chose not to introduce the mRNA state between transcription and translation in our model. We presented things as if a protein would act directly upon the following. |
= Conclusion = | = Conclusion = | ||
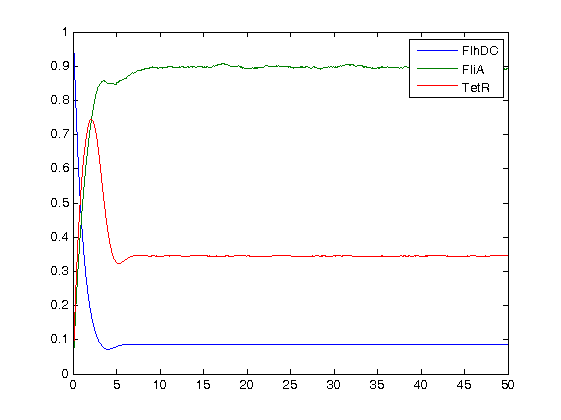
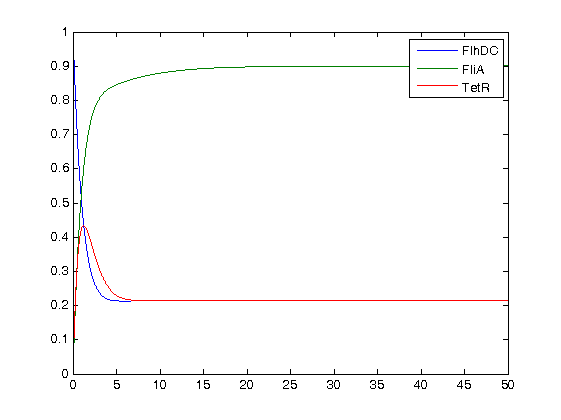
We finally obtained the following equations : | We finally obtained the following equations : | ||
| - | |||
[[Image:FliA_dynamics.jpg|center]] | [[Image:FliA_dynamics.jpg|center]] | ||
[[Image:CFP.jpg|center]] | [[Image:CFP.jpg|center]] | ||
[[Image:YFP.jpg|center]] | [[Image:YFP.jpg|center]] | ||
[[Image:eqn_EnvZ-RFP.jpg|center]] | [[Image:eqn_EnvZ-RFP.jpg|center]] | ||
| + | [[Image:eqn_flhDC.jpg|center]] | ||
| + | |||
and the following parameters : | and the following parameters : | ||
| Line 139: | Line 139: | ||
|}</center> | |}</center> | ||
| - | Now you have had a good overlook of our model, go see a more | + | Now you have had a good overlook of our model, go see a more detailed justification where our normalization choices are thouroughly explained : |
| - | + | {{Paris/Toggle|Detailed justification|Team:Paris/Network_analysis_and_design/Core_system/Model_construction/Detailed_justification}} | |
| - | + | ||
| + | Moreover, in order to take into account the fact that data are obtained form 'real' experiments (number of parameters, length of data set) we hereby propose a '''criteria to legitimate the chosen model depending on the experimental conditions''', in comparison with a more general model (Hill functions). | ||
| - | + | {{Paris/Toggle|Akaike Criteria|Team:Paris/Network_analysis_and_design/Core_system/Model_construction/Akaike}} | |
| - | + | ||
| - | + | {{Paris/Navig|Team:Paris/Analysis}} | |
= Bibliography = | = Bibliography = | ||
* [1] Shiraz Kalir, Uri Alon. ''Using quantitative blueprint to reprogram the dynamics of the flagella network.'' Cell, June 11, 2004, Vol.117, 713-720. | * [1] Shiraz Kalir, Uri Alon. ''Using quantitative blueprint to reprogram the dynamics of the flagella network.'' Cell, June 11, 2004, Vol.117, 713-720. | ||
Latest revision as of 00:42, 30 October 2008
|
Model Construction
Other pages:
Introduction
Classical model and temporal rescaling
ConclusionWe finally obtained the following equations :
Now you have had a good overlook of our model, go see a more detailed justification where our normalization choices are thouroughly explained : ↓ Detailed justification ↑
Moreover, in order to take into account the fact that data are obtained form 'real' experiments (number of parameters, length of data set) we hereby propose a criteria to legitimate the chosen model depending on the experimental conditions, in comparison with a more general model (Hill functions). ↓ Akaike Criteria ↑
Bibliography
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 "
"