Team:Paris/Analysis/Model2 Analysis
From 2008.igem.org
(→Model Analysis) |
(→Conclusion) |
||
| (15 intermediate revisions not shown) | |||
| Line 1: | Line 1: | ||
{{Paris/Menu}} | {{Paris/Menu}} | ||
| - | {{Paris/Header| | + | {{Paris/Header|System Improvements Analysis}} |
| - | + | {{Paris/Section_contents_analysis}} | |
| - | === | + | |
| + | == System Improvements Analysis == | ||
| + | |||
| + | === HSL mediated coupled oscillators === | ||
==== Parameter search ==== | ==== Parameter search ==== | ||
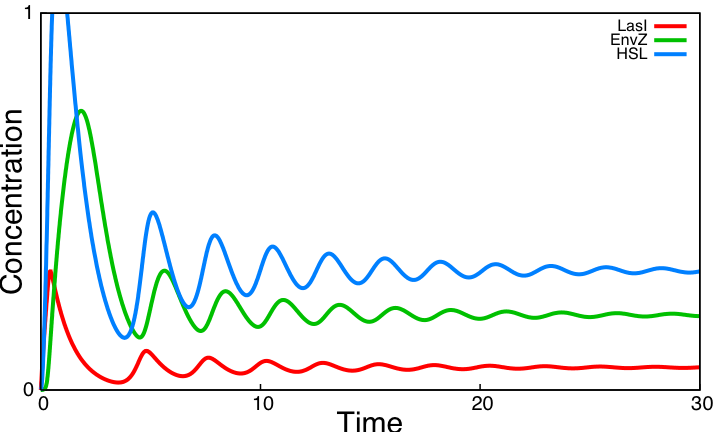
| - | In this system we rely on kinetic parameter values taken from the literature. However, three kinetic parameters remain unknown : HSL production rate (β<sub>HSL</sub>), the threshold value of HSL above which EnvZ is expressed (θ<sub>HSL</sub>) and the threshold value of EnvZ above which lasI is inhibited (θ<sub>EnvZ</sub>). We assume, as [[Team:Paris/Bibliography|[2]]] did, that | + | In this system we rely on kinetic parameter values taken from the literature. However, three kinetic parameters remain unknown : HSL production rate (β<sub>HSL</sub>), the threshold value of HSL above which EnvZ is expressed (θ<sub>HSL</sub>) and the threshold value of EnvZ above which lasI is inhibited (θ<sub>EnvZ</sub>). The two modules of the coupled oscillators are the the negative loop involving HSL, and the core system. We assume, as [[Team:Paris/Bibliography|[2]]] did, that the HSL negative loop considered alone is functional and thus look for values of these three parameters such that concentration values of species in this loop oscillate. This parameter search as well as simulations on this page are done using the modeling environment [http://contraintes.inria.fr/BIOCHAM/ BIOCHAM]. |
For the HSL production rate we find that HSL time scale has to be similar to lasI time scale. As HSL is produced only in cells but is degraded inside and outside cells, the following relation where c is the proportion of the total volume occupied by cells is required : | For the HSL production rate we find that HSL time scale has to be similar to lasI time scale. As HSL is produced only in cells but is degraded inside and outside cells, the following relation where c is the proportion of the total volume occupied by cells is required : | ||
| Line 15: | Line 18: | ||
[[Image:System0.png|400px|center|thumb|Simulation of the HSL loop]] | [[Image:System0.png|400px|center|thumb|Simulation of the HSL loop]] | ||
| - | For all forthcoming simulations where the interactions in this loop | + | For all forthcoming simulations where the interactions in this loop appear, we make use of the parameter values deducted from this parameter search. |
==== Coupling results ==== | ==== Coupling results ==== | ||
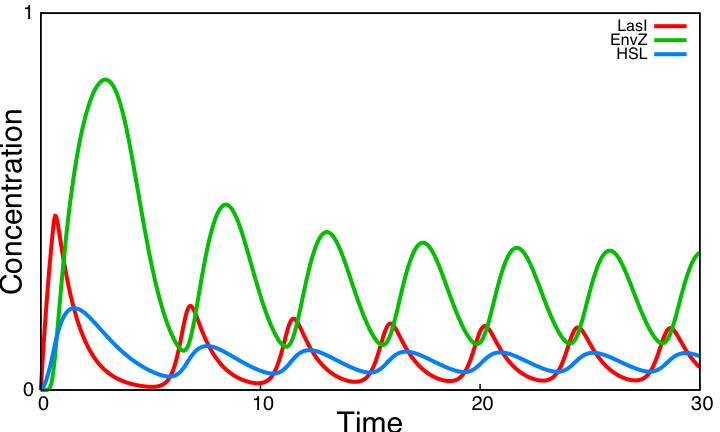
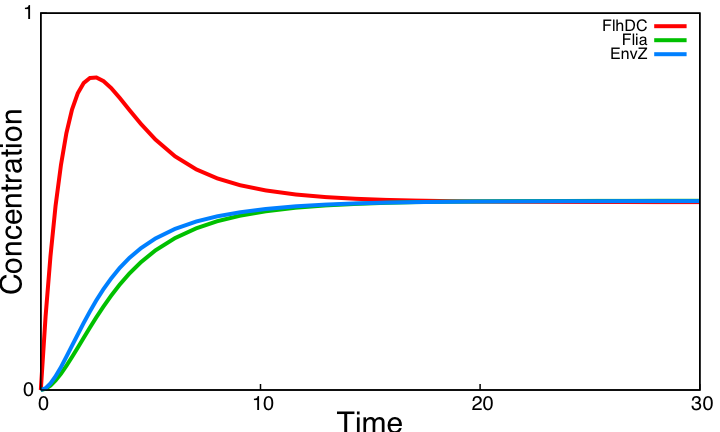
| - | The two modules of the | + | The two modules of the coupled oscillators system are coupled by EnvZ. The HSL negative loop is functional whereas the core system is not. We compare below the behavior of the core system alone to the behavior of the system coupling these two modules. |
| - | The HSL | + | |
[[Image:Core0.png|400px|left|thumb|Simulation of the core system]] | [[Image:Core0.png|400px|left|thumb|Simulation of the core system]] | ||
| - | [[Image:System4.png|400px|right|thumb|Simulation of the | + | [[Image:System4.png|400px|right|thumb|Simulation of the coupled oscillators system]] |
<br> | <br> | ||
| Line 45: | Line 47: | ||
Coupling these two modules has a positive effect on the overall behavior but it still does not provide sustained oscillations. The core system interfere with the behavior of the HSL module and the HSL module is not strong enough to retain its oscillatory behavior. | Coupling these two modules has a positive effect on the overall behavior but it still does not provide sustained oscillations. The core system interfere with the behavior of the HSL module and the HSL module is not strong enough to retain its oscillatory behavior. | ||
| - | It seems that obtaining oscillations by coupling two modules is possible only if each module taken separately is functional. | + | It seems that obtaining oscillations by coupling two modules is possible only if each module taken separately is functional. |
| - | + | === HSL mediated simple oscillator === | |
| - | === | + | |
==== Oscillations ==== | ==== Oscillations ==== | ||
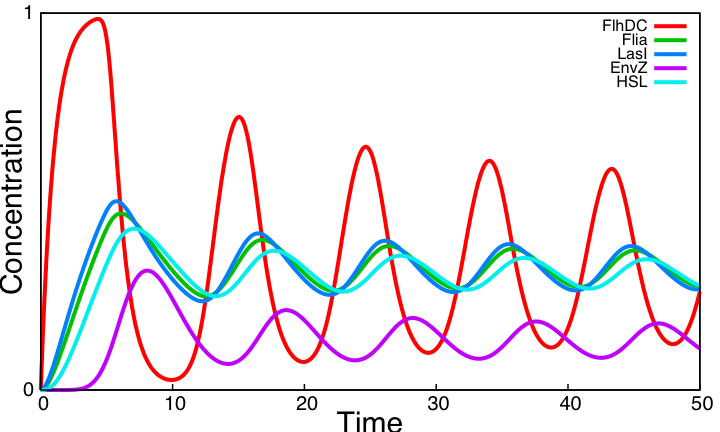
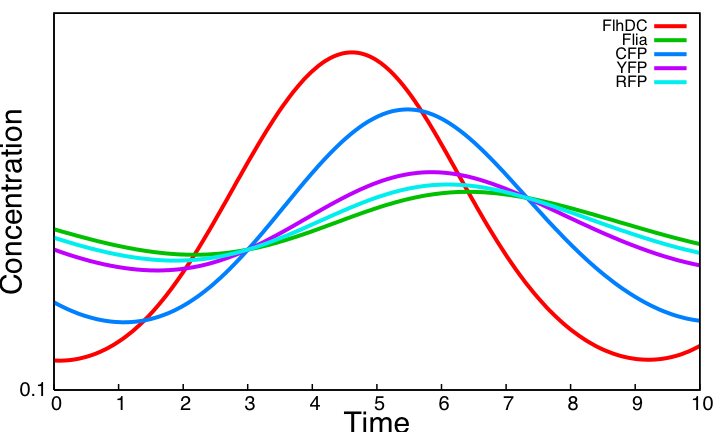
| - | We | + | We now consider the simple oscillator system. Its kinetic parameter values are obtained from the literature and from the parameter search carried above for the three unknown parameters in common with the HSL module. Here is the simulation obtained. |
| - | [[Image:System2.png|400px|center|thumb|Simulation of the | + | [[Image:System2.png|400px|center|thumb|Simulation of the HSL mediated simple oscillator]] |
This system shows sustained oscillations. It is worth noticing that this is obtained without removing the auto-activation loop on Flia and the activation of lasI by FlhDC even though these two interactions hamper the oscillatory behavior as shown in the analysis of the core system. | This system shows sustained oscillations. It is worth noticing that this is obtained without removing the auto-activation loop on Flia and the activation of lasI by FlhDC even though these two interactions hamper the oscillatory behavior as shown in the analysis of the core system. | ||
==== FIFO ==== | ==== FIFO ==== | ||
| - | All FIFO related interactions of the core system remain in the | + | All FIFO related interactions of the core system remain in the HSL mediated simple oscillator. The behavior is therefore the same as observed in the core system. But whereas one had to impose FlhDC as a step function in the core system to be able to observe the FIFO behavior, FlhDC oscillatons are here inherent to the dynamics of the system. Below is a close-up view of |
| - | FIFO reporters concentrations for one period of the | + | FIFO reporters concentrations for one period of the HSL mediated simple oscillator : |
| - | [[Image:S2fifo.png|400px|center|thumb|FIFO behavior in the | + | [[Image:S2fifo.png|400px|center|thumb|FIFO behavior in the HSL mediated simple oscillator]] |
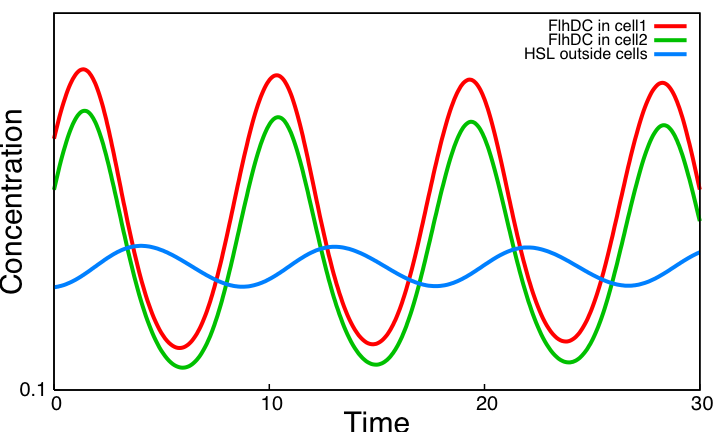
==== Synchronization ==== | ==== Synchronization ==== | ||
| Line 71: | Line 72: | ||
== Conclusion == | == Conclusion == | ||
| - | The above simulations imply that the HSL mediated simple oscillator system should be preferred as it provides sustained oscillation as opposed to the | + | The above simulations imply that the HSL mediated simple oscillator system should be preferred as it provides sustained oscillation as opposed to the coupled oscillators. Note that this result not only shows that the system can work for some arbitrary kinetic parameter values. As almost all parameters are taken form the literature, it reveals that for biologically compatible parameter values, the system should work. In addition a population of cells implementing the simple oscillator system can be synchronized by quorum sensing. |
| + | |||
| + | |||
| + | {{Paris/Navig|Team:Paris/Analysis}} | ||
Latest revision as of 03:05, 30 October 2008
|
System Improvements Analysis
Other pages:
System Improvements AnalysisHSL mediated coupled oscillatorsParameter searchIn this system we rely on kinetic parameter values taken from the literature. However, three kinetic parameters remain unknown : HSL production rate (βHSL), the threshold value of HSL above which EnvZ is expressed (θHSL) and the threshold value of EnvZ above which lasI is inhibited (θEnvZ). The two modules of the coupled oscillators are the the negative loop involving HSL, and the core system. We assume, as [2] did, that the HSL negative loop considered alone is functional and thus look for values of these three parameters such that concentration values of species in this loop oscillate. This parameter search as well as simulations on this page are done using the modeling environment [http://contraintes.inria.fr/BIOCHAM/ BIOCHAM]. For the HSL production rate we find that HSL time scale has to be similar to lasI time scale. As HSL is produced only in cells but is degraded inside and outside cells, the following relation where c is the proportion of the total volume occupied by cells is required :
Besides, we observe that the threshold value of EnvZ needs to be low and that the loop is functional for any threshold value of HSL. For three parameter values validating these requirements (βHSL=16, θEnvZ=0.1, θHSL=0.5), the HSL loop alone has the following behavior : For all forthcoming simulations where the interactions in this loop appear, we make use of the parameter values deducted from this parameter search. Coupling resultsThe two modules of the coupled oscillators system are coupled by EnvZ. The HSL negative loop is functional whereas the core system is not. We compare below the behavior of the core system alone to the behavior of the system coupling these two modules.
HSL mediated simple oscillatorOscillationsWe now consider the simple oscillator system. Its kinetic parameter values are obtained from the literature and from the parameter search carried above for the three unknown parameters in common with the HSL module. Here is the simulation obtained. This system shows sustained oscillations. It is worth noticing that this is obtained without removing the auto-activation loop on Flia and the activation of lasI by FlhDC even though these two interactions hamper the oscillatory behavior as shown in the analysis of the core system. FIFOAll FIFO related interactions of the core system remain in the HSL mediated simple oscillator. The behavior is therefore the same as observed in the core system. But whereas one had to impose FlhDC as a step function in the core system to be able to observe the FIFO behavior, FlhDC oscillatons are here inherent to the dynamics of the system. Below is a close-up view of FIFO reporters concentrations for one period of the HSL mediated simple oscillator : SynchronizationTo assess synchronization capabilities we mix two population of cells in the chemostat, one having a slightly higher degradation rate of all proteins. This entails different period and amplitude of oscillations. However, HSL oscillations outside cells enable oscillations to remain synchronized. Simulations reveal parameter η is a key parameter : it controls the pace at which HSL diffuses between cells and the environment. A low η value disrupt both synchronization capabilities and the oscillatory behavior. With the value η=505 taken from [2] oscillations are sustained and synchronized across cell population. ConclusionThe above simulations imply that the HSL mediated simple oscillator system should be preferred as it provides sustained oscillation as opposed to the coupled oscillators. Note that this result not only shows that the system can work for some arbitrary kinetic parameter values. As almost all parameters are taken form the literature, it reveals that for biologically compatible parameter values, the system should work. In addition a population of cells implementing the simple oscillator system can be synchronized by quorum sensing.
|
 "
"