Team:Paris/Modeling/BOB
From 2008.igem.org
(Difference between revisions)
(→Population evolution) |
|||
| Line 6: | Line 6: | ||
* This preliminary approach is mainly based on a bibliographical work. In fact, it is important to understand that with this approach, we did not intend to design the most accurate model possible. We found essential to choose only parameters that we could determine or control in the wet lab. The main goal was to get quickly a first idea of the way our system could behave. | * This preliminary approach is mainly based on a bibliographical work. In fact, it is important to understand that with this approach, we did not intend to design the most accurate model possible. We found essential to choose only parameters that we could determine or control in the wet lab. The main goal was to get quickly a first idea of the way our system could behave. | ||
* The goal here is to present the differential equations we used in the model. At each step we shall describe why we chose these precise equations, the drawbacks and possible improvements, the parameters involved and eventually a biologically coherent value. | * The goal here is to present the differential equations we used in the model. At each step we shall describe why we chose these precise equations, the drawbacks and possible improvements, the parameters involved and eventually a biologically coherent value. | ||
| - | |||
| - | |||
=Bibliography= | =Bibliography= | ||
| Line 37: | Line 35: | ||
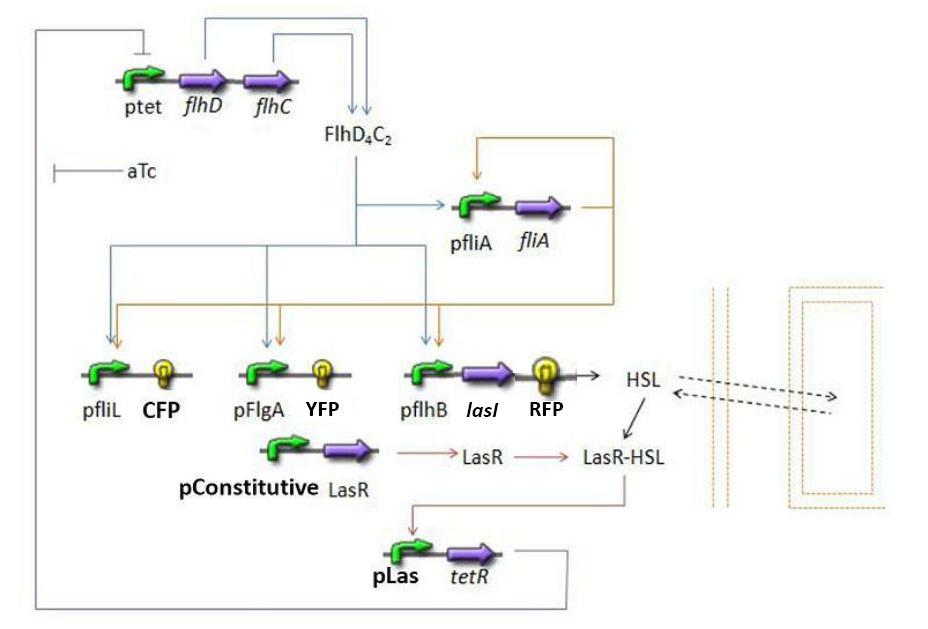
= Establishing the model = | = Establishing the model = | ||
| + | [[Image:Globalmodel.jpg|600px|las System|center]] | ||
== Population evolution == | == Population evolution == | ||
First of all, it seems important at this stage to present the way we interpret the evolution of the population in the chemostat. We want to impose to our model the fact that the rate of production has to be proportional to the existing population and to the amount of available resources. Hence a logistic model of the population, where c denotes the concentration of cells in the medium: | First of all, it seems important at this stage to present the way we interpret the evolution of the population in the chemostat. We want to impose to our model the fact that the rate of production has to be proportional to the existing population and to the amount of available resources. Hence a logistic model of the population, where c denotes the concentration of cells in the medium: | ||
Revision as of 16:22, 27 August 2008
Introduction
BibliographyMuch of our inspiration comes from four articles to which we shall refer in the next subsections :
Summary of the steps modeledHere is a quick summary of the step we decided to interpret mathematically...
Establishing the modelPopulation evolutionFirst of all, it seems important at this stage to present the way we interpret the evolution of the population in the chemostat. We want to impose to our model the fact that the rate of production has to be proportional to the existing population and to the amount of available resources. Hence a logistic model of the population, where c denotes the concentration of cells in the medium: Then, we need to add the death term, and a dilution term cause by the renewal of the chemostat. Finally we get : FIFO temporal order Module(lien partie model) Steps involvedMathematical modelDiscussionNormalizationWhich gene goes were?Simulations and ResultsSynchronization Module : las System(lien partie model) Steps involvedMathematical ModelDynamics of HSLDynamics of HSLextTetR=f(HSL)FlhDC=f(TetR)Simulations and resultsParameters summaryTesting the oscillationsTesting the FIFOTesting the Synchronization |
 "
"