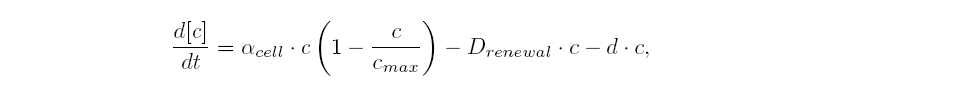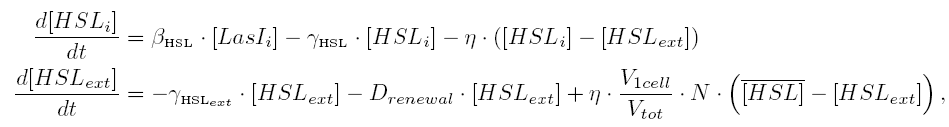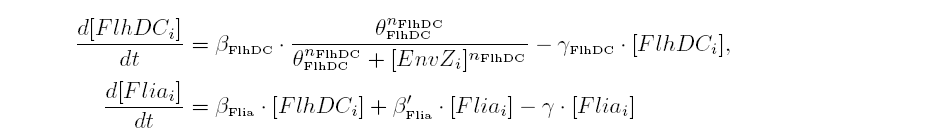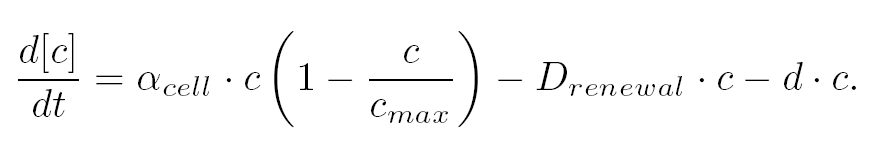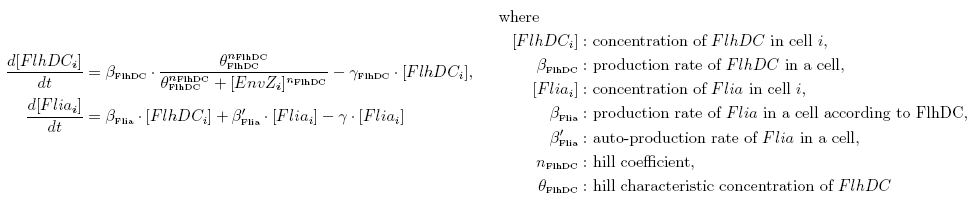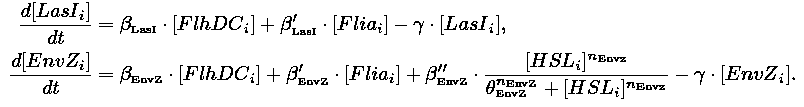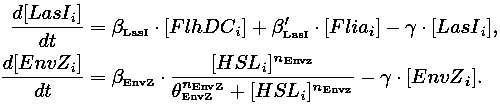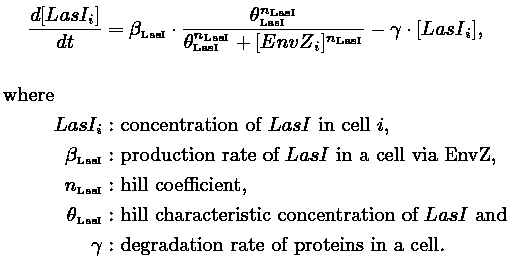Team:Paris/Analysis/Construction2
From 2008.igem.org
(→Introduction) |
(→Introduction) |
||
| Line 6: | Line 6: | ||
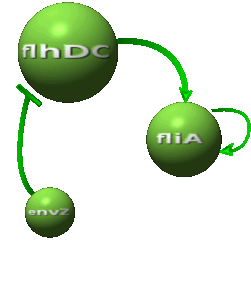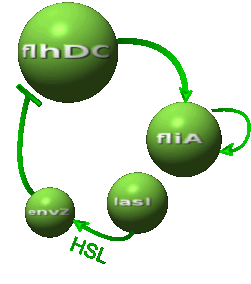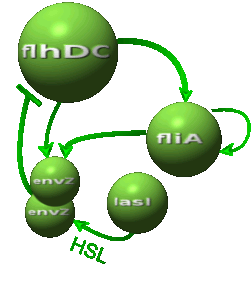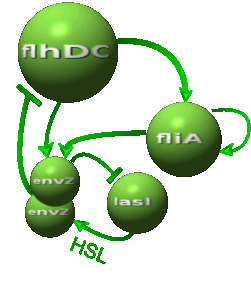
In this section, we investigate possible improvements of the [[Team:Paris/Network_analysis_and_design/Core_system/Model_construction|core system]]. Our objective is twofold : the system has to provide sustained oscillations and these oscillations should be synchronized amongst a population of cells. To this aim we explore designs inspired by quorum sensing and model in a chemostat cell growth and species diffusion outside cells. We consider two models relying on different designs principles. | In this section, we investigate possible improvements of the [[Team:Paris/Network_analysis_and_design/Core_system/Model_construction|core system]]. Our objective is twofold : the system has to provide sustained oscillations and these oscillations should be synchronized amongst a population of cells. To this aim we explore designs inspired by quorum sensing and model in a chemostat cell growth and species diffusion outside cells. We consider two models relying on different designs principles. | ||
| - | + | ||
| - | {{Paris/Toggle|To join our quest for alternatives click here!|Team:Paris/ | + | {{Paris/Toggle|To join our quest for alternatives click here!|Team:Paris/DescriptionMoreModelConstruction2}} |
| - | + | ||
{|align="center" | {|align="center" | ||
| Line 14: | Line 14: | ||
! colspan="2" |Same environment | ! colspan="2" |Same environment | ||
|- style="text-align:center" | |- style="text-align:center" | ||
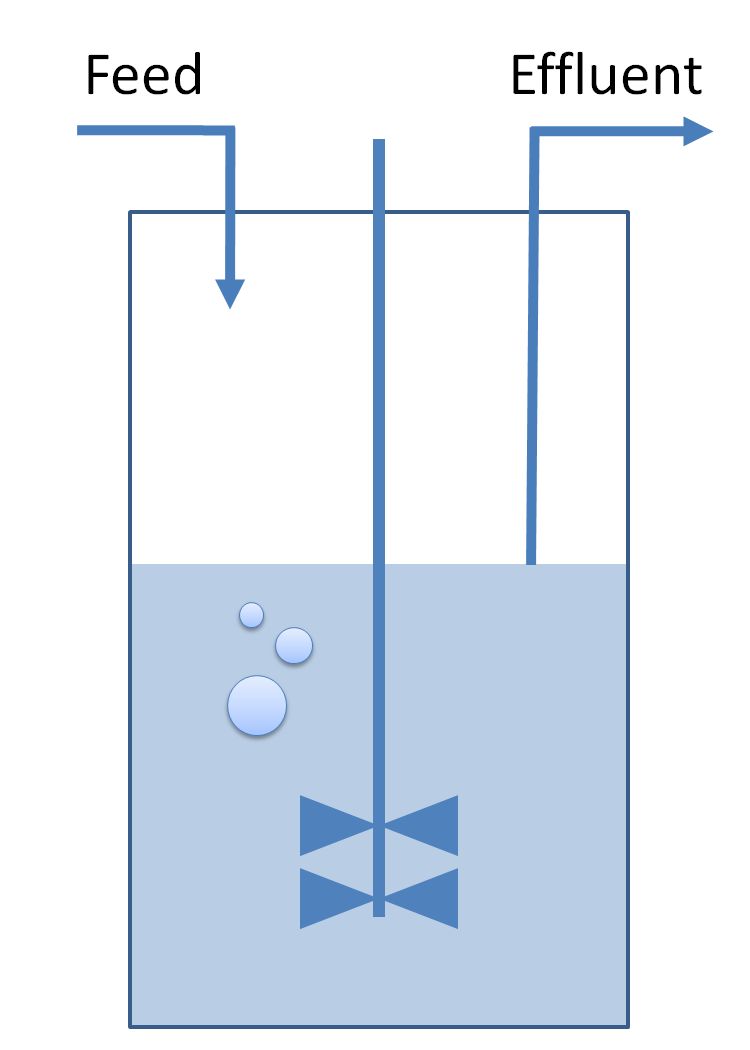
| - | |[[Image:chemostat.png|center|120px]] Using a chemostat | + | |<center>[[Image:chemostat.png|center|120px]] Using a chemostat</center> |
|- style="background: #649CD7; text-align: center;" | |- style="background: #649CD7; text-align: center;" | ||
! colspan="2" |Same starting point, different synchronization mechanisms | ! colspan="2" |Same starting point, different synchronization mechanisms | ||
Revision as of 03:17, 30 October 2008
|
System Improvements Description
Other pages:
IntroductionIn this section, we investigate possible improvements of the core system. Our objective is twofold : the system has to provide sustained oscillations and these oscillations should be synchronized amongst a population of cells. To this aim we explore designs inspired by quorum sensing and model in a chemostat cell growth and species diffusion outside cells. We consider two models relying on different designs principles. ↓ To join our quest for alternatives click here! ↑
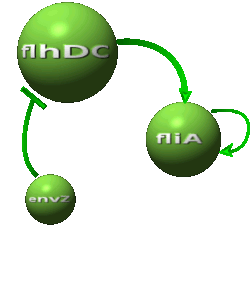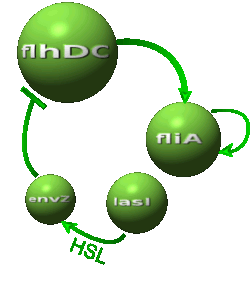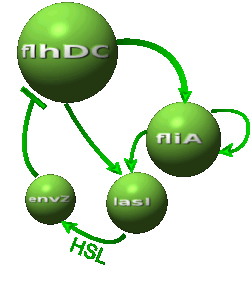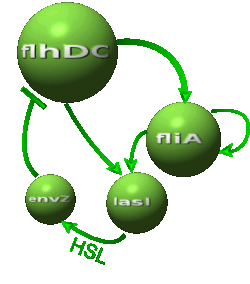
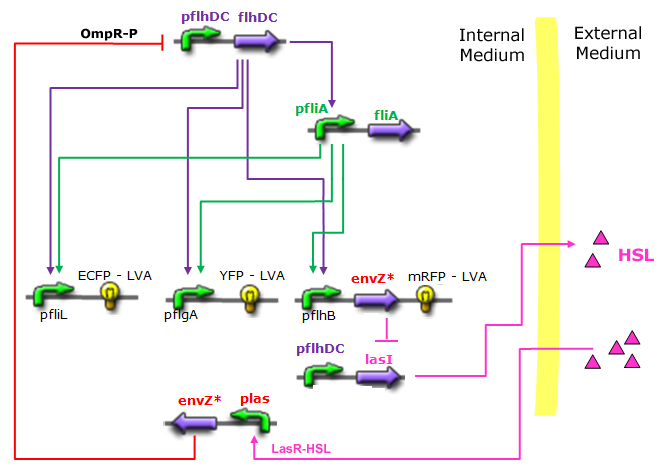
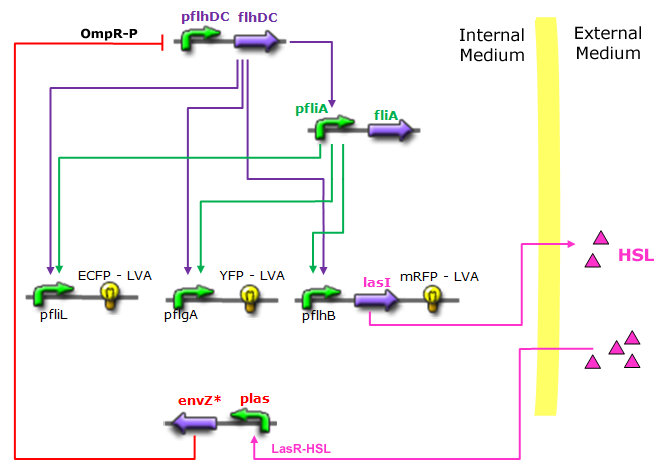
Modeling AlternativesThe proposed systems are:
Both the coupled and simple oscillators describe events that happen not only at the cellular level (as in the core system) but also at the population level due to interactions needed between a cell and its environment. In the following sections, we first describe the common part among the two proposed models and then focus our attention to the alternatives description where the characteristics that are specific to each of the modeling alternatives are presented. Common Description
↓ read more on common dynamics... ↑
Alternatives Description
↓ read more on alternatives description... ↑
Kinetic parameter valuesRemarkably, almost all parameter values are available from experimental measurements in [1] and from the work of Garcia-Ojalvo in [2]. Additionally minimizing the number of parameters is possible by rescaling as done for the core system. Relevant values for the sole two missing parameters are found by exploiting a modularity assumption as described in the next section. The following table summarize our findings:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 "
"