Team:BrownTwo/Limiter/modeling
From 2008.igem.org
(→Motivation for Modeling) |
(→Hill equation) |
||
| Line 13: | Line 13: | ||
We have modeled all gene products in our system using the following equations. | We have modeled all gene products in our system using the following equations. | ||
| - | [[Image:]] | + | [[Image:Simple_diagram.png|center|800px]] |
| - | [[Image:]] | + | [[Image:alpha_y_=_0.jpg]] |
| - | [[Image:]] | + | [[Image:alpha_y_=_2.5.jpg]] |
| + | |||
| + | [[Image:alpha_y_=_5.jpg]] | ||
| + | |||
| + | [[Image:alpha_y_=_7.5.jpg]] | ||
| + | |||
| + | [[Image:alpha_y_=_10.jpg]] | ||
| + | |||
| + | [[Image:Equations_galore.png|center|800px]] | ||
Revision as of 03:43, 30 October 2008
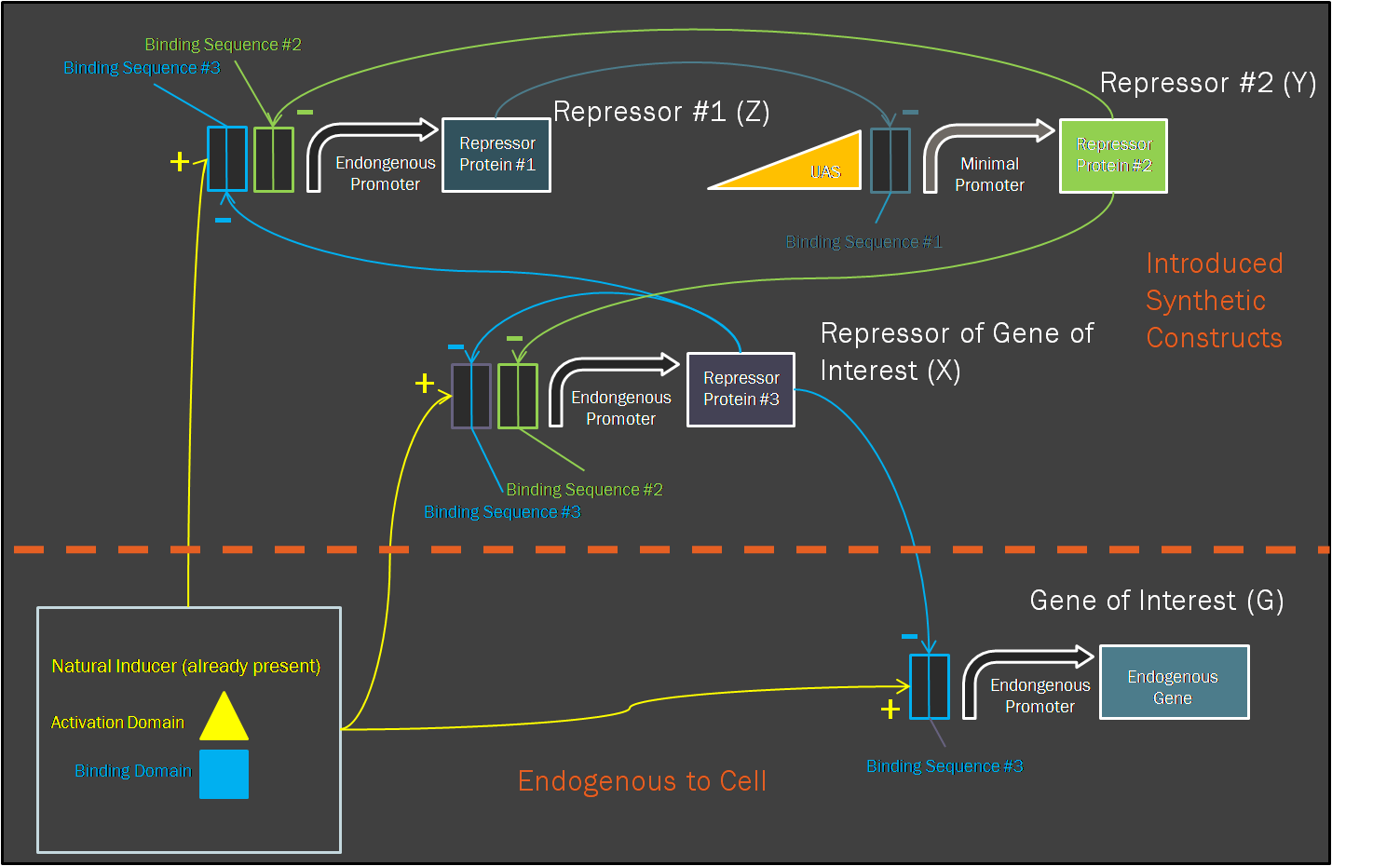
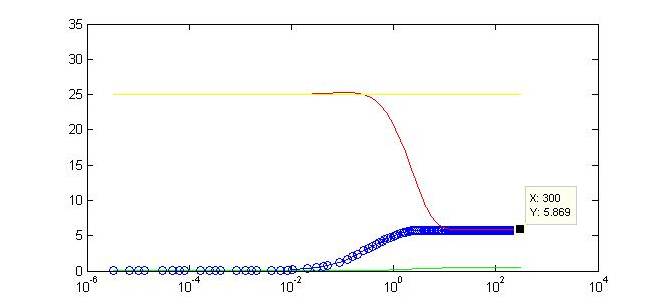
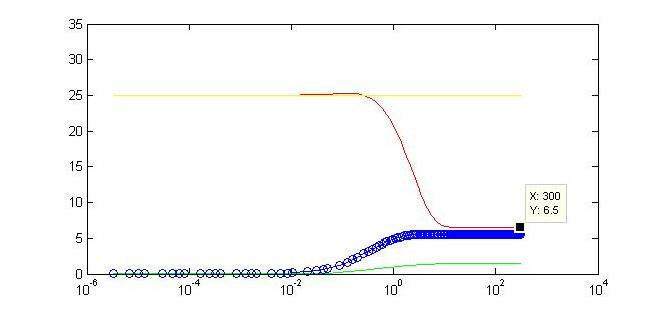
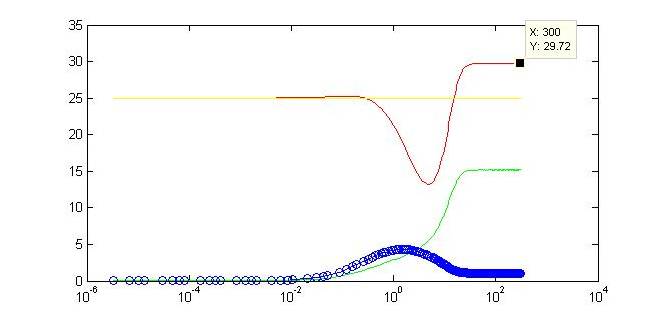
Motivation for ModelingIn contrast to pure experimentation, modeling allows for the rational design of synthetic biological systems. Part characterization makes it possible to apply the known activity of genetic parts to developing a prediction of their qualitative behavior when they are pieced together into a composite device. Such an approach was aptly demonstrated in the paper by Dr. Ajo-Franklin (Ajo-Franklin et al., 2007). They generated a Hill equation model for composite system, to which they applied experimentally-quantified values for the parameters representing the individual parts in the system. Their predictions with this approach matched up considerably well to measurements they made once they have built their final device. Seeing as we incorporating many of the same parts into our own limiter network, we decided to modify their Hill equations to suit our particular design. It was important for us to model our system because it was necessary to ascertain, given the complexity of the transcriptional interactions, whether the design would generate our desired threshold-driven output. Hill equationAccording to a Hill equation, it is possible to model the relationship between a gene (G) and its transcription factor. The equation varies slightly depending upon whether the transcription factor has an activating or inhibitory effect. We have modeled all gene products in our system using the following equations. |
 "
"