Introduction

• The key problem with a dynamic system consists in the fact that adding a new equation gives a more detailed idea of the overall process, but one looses meaning by doing so since new undefined parameters appear. Hence, it becomes hard to link those parameters with a biological meaning and reality.
• In that respect we chose to build at first a simplified model, which would enable us to help us understand the processes implied in the system. In that respect, we chose not to introduce the mRNA state between transcription and translation in our model. We presented things as if a protein would act directly upon the following. Furthermore, we assumed that describing routinely every step, would only force us into finding more parameters.
• This preliminary approach is mainly based on a bibliographical work. In fact, it is important to understand that with this approach, we did not intend to design the most accurate model possible. We found essential to choose only parameters that we could determine or control in the wet lab. The main goal was to get quickly a first idea of the way our system could behave.
• The goal here is to present the differential equations we used in the model. At each step we shall describe why we chose these precise equations, the drawbacks and possible improvements, the parameters involved and eventually a biologically coherent value.

Bibliography

Much of our inspiration comes from four articles to which we shall refer in the next subsections :

• [1] Shiraz Kalir, Uri Alon. Using quantitative blueprint to reprogram the dynamics of the flagella network. Cell, June 11, 2004, Vol.117, 713-720.
• [2]Jordi Garcia-Ojalvo, Michael B. Elowitz, Steven H. Strogratz. Modeling a synthetic multicellular clock : repressilators coupled by quorum sensing. PNAS, July 27, 2004, Vol. 101, no. 30.
• [3]Nitzan Rosenfeld, Uri Alon. Response delays and the structure of transcription networks. JMB, 2003, 329, 645-654.
• [4]Nitzan Rosenfeld, Michael B. Elowitz, Uri Alon. Negative autoregulation speeds the response times of transcription networks. JMB, 2003, 323, 785-793.
• [5]S.Kalir, J. McClure, K. Pabbaraju, C. Southward, M. Ronen, S. Leibler, M. G. Surette, U. Alon. Ordering genes in a flagella pathway by analysis of expression kinetics from living bacteria. Science, June 2001, Vol 292.

Summary of the steps modeled

Here is a quick summary of the step we decided to interpret mathematically...

• FIFO temporal order system
  • FliA behind pFliA= f(FlhDC,FliA)
  • CFP behind pFliL = f(FlhDC,FliA)
  • YFP behind pFliL = f(FlhDC,FliA)
  • RFP and LasI behind pFliL = f(FlhDC,FliA)
• Synchronisation : las system
  • HSL = f(LasI)
  • HSL ⇋ HSLext
  • TetR = f(HSL)
  • FlhDC = f(TetR)
• Synchronisation : lux system
  • HSL = f(LasI)
  • HSL ⇋ HSLext
  • TetR = f(HSL)
  • FlhDC = f(TetR)

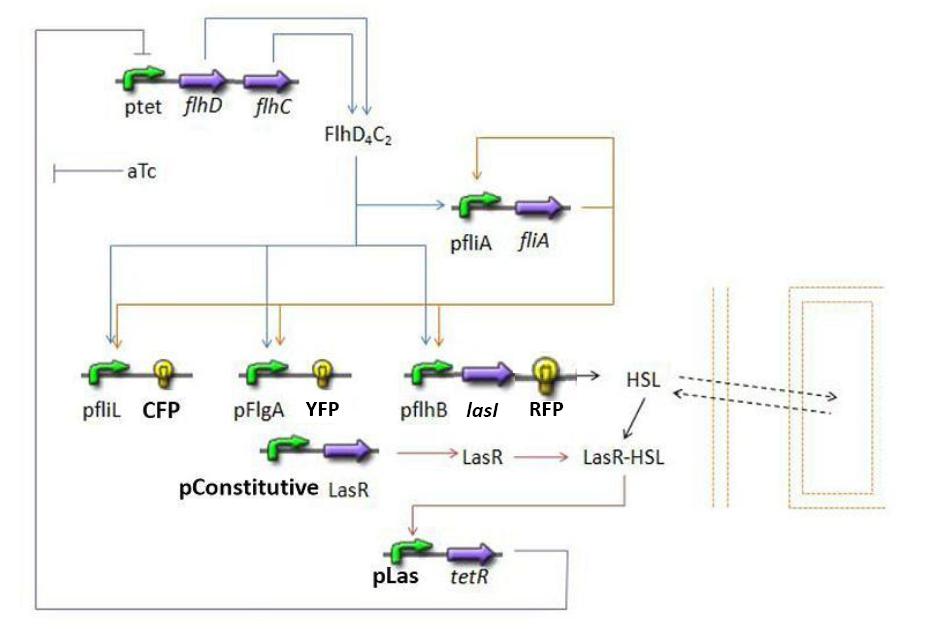
Establishing the model

Population evolution

First of all, it seems important at this stage to present the way we interpret the evolution of the population in the chemostat. We want to impose to our model the fact that the rate of production has to be proportional to the existing population and to the amount of available resources. Hence a logistic model of the population, where c denotes the concentration of cells in the medium:

Then, we need to add the death term, and a dilution term cause by the renewal of the chemostat. Finally we get :

Where c_max is the carrying capacity for cell growth, and D the dilution rate, d the death rate constant

FIFO Temporal Order Module

Informations about the FIFO Temporal Order module

Steps involved

• FliA behind pFliA= f(FlhDC,FliA)
• CFP behind pFliL = f(FlhDC,FliA)
• YFP behind pFliL = f(FlhDC,FliA)
• RFP and LasI behind pFliL = f(FlhDC,FliA)

Mathematical model

Classically we use the following equation to model gene interactions :

where [Y] denotes the concentration of Y protein and γ its degradation rate (which unit is time^-1).
Yet, the flagella gene network has been thoroughly studied in [1]. We used two major results presented in this study. Firstly, Shiraz Kalir and Uri Alon came up with the fact that the promoters of class 2 genes, among which fliL, flgA and flhB, behaved like SUM-gate functions with flhDC and fliA inputs. Secondly, their experiments proved that these influences could be considered as linear. Thus the following model:

β and β’ represent the relative influence of flhDC and fliA respectively, the units of β and β’ being time-1.
Furthermore, they came up with numerical values of β and β’ for each gene, which fitted quite well to their experiments. We then decided that we could use those values as well in our model.
Finally, here are our final equations:

Discussion

Normalization

Which gene goes were?

Simulations and Results

Synchronization Module

Using Las system

Steps involved

Mathematical Model

Dynamics of HSL

Dynamics of HSL_ext

TetR=f(HSL)

FlhDC=f(TetR)

Using Lux system

fliA = f(FlhDC,FliA) (1) RFP and lasI behind pFliL = f(FlhDC,FliA) (2) Influence of lasI over HSL (3) Relation between HSL and HSLext (4) Influence of HSL over tetR (5) flhDC = f(tetR) (6)

4.3.2 Mathematical model First of all, we naturally keep the same model for steps (1) and (2).

4.3.2.1 Dynamics of HSL First and foremost, HSL is the key element in the synchronization process. We used a diffusive specie in order to balance the concentrations between cells. The outside medium concentration becomes an intermediate variable. We ended with

Where is the diffusion rate expressed in time-1 and

Then, we had two choices to model this step. At first we were inspired by [2] where the production of HSLint is described as being linear, and we were given the value of the constant. However, the results presented in this study were introduced as only being theoretical. The degradation rate comes in quite naturally.

We chose to model the creation of HSL by a Michaelis Menten expression. In fact, we found out that lasI seemed to be a monomeric enzyme, thus setting the Hill parameter to 1.

Here, is expressed in the concentration unit, and in the concentration unit by time unit.

It is important to note that we took into account the fact that lasR/(lasR linked to HSL) was a function of HSL. However, we assumed that the fraction of HSL bound to lasR would not influence HSL concentration; this is the reason why, no “degradation due to binding term” appears in the HSL model.

4.3.2.2 Dynamics of HSLext The evolution of HSLext may be described with three terms. First of all, there is a dilution rate, Drenewal, due to the renewal of the chemostat. There is the usual degradation rate, .

Which gives

where

4.3.2.3 TetR = f(HSL) Here we had the choice to model the complexation phase of HSL and lasR, and then the binding phase of this complex on the pLas promoter. We assumed that those stages were short, and then decided to model them by a single step.

We checked in the registry that the pLas sequence was the same as in [promoter specificity]. It is explained that there are two operators, denoted OP1 and OP2. The Hill parameters were detailed in this article, hence our modeling choice :

4.3.2.4 FlhDC = f(TetR) For this last step, since we have not found any article indicating that we could simplify the model by using a linear function. Then, we chose a complete Hill function to describe the dynamics of flhDC:

4.3.3 Experiment and discussion

Parameters summary

Results

Oscillations

FIFO

Synchronization