Team:Paris/Modeling/BOB
From 2008.igem.org
(→Dynamics of HSL) |
|||
| Line 13: | Line 13: | ||
The goal here is to present the differential equations we used in the model. At each step we shall describe why we chose these precise equations, the drawbacks and possible improvements, the parameters involved and eventually a biologically coherent value. | The goal here is to present the differential equations we used in the model. At each step we shall describe why we chose these precise equations, the drawbacks and possible improvements, the parameters involved and eventually a biologically coherent value. | ||
| + | |||
| + | = Model = | ||
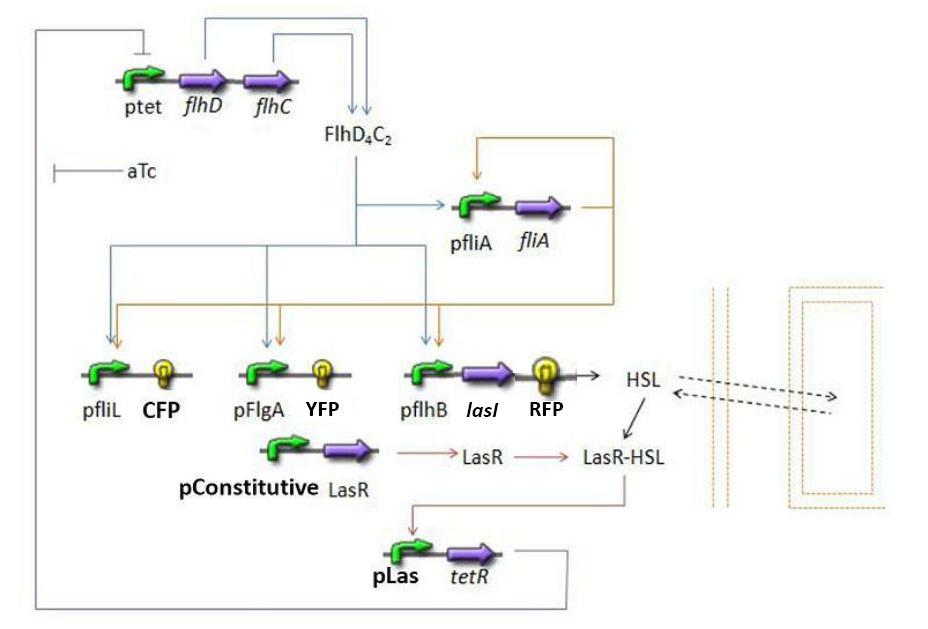
| + | * Here is an overall view of the whole system : | ||
| + | [[Image:Globalmodel.jpg|600px|center]] | ||
== Steps of the Model == | == Steps of the Model == | ||
| - | + | We chose to broke up this system in three sub systems for presentation clarity | |
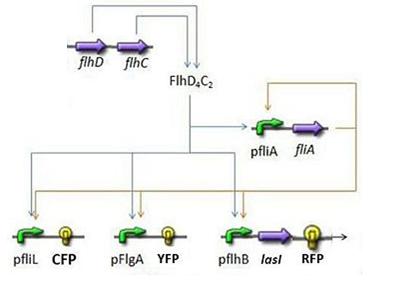
| + | * First Subsystem | ||
| + | [[Image:Subsystem1.jpg|center]] | ||
| + | ** FliA behind pFliA= f(FlhDC,FliA) | ||
| + | ** CFP behind pFliL = f(FlhDC,FliA) | ||
| + | ** YFP behind pFliL = f(FlhDC,FliA) | ||
| + | ** RFP and LasI behind pFliL = f(FlhDC,FliA) | ||
| + | [[Team:Paris/Project/FIFO|see also FIFO module]] | ||
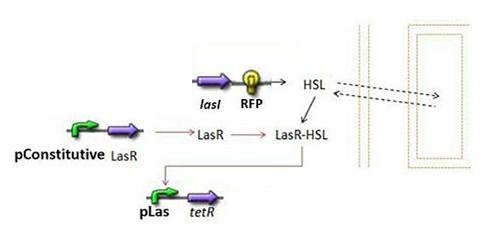
| - | [[ | + | * Second Subsystem |
| - | * | + | [[Image:Subsystem2.jpg|center]] |
| - | + | ** HSL = f(LasI) or f(LuxI) depending on which system is being used | |
| - | * | + | ** HSL ⇋ HSLext |
| - | * | + | ** TetR = f(HSL) |
| + | [[Team:Paris/Project/Synchronisation|see also Synchronisation module]] | ||
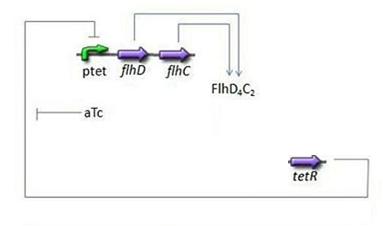
| - | + | * Third Subsystem | |
| - | * | + | [[Image:Subsystem3.jpg|center]] |
| - | + | ** FlhDC = f(TetR) | |
| - | + | ||
| - | [[ | + | |
| - | * FlhDC = f(TetR) | + | |
| - | |||
| - | |||
== Population evolution == | == Population evolution == | ||
* First of all, it seems important at this stage to present the way we interpret the evolution of the population in the chemostat. We want to impose to our model the fact that the rate of production has to be proportional to the existing population and to the amount of available resources. Hence a logistic model of the population, where c denotes the concentration of cells in the medium: | * First of all, it seems important at this stage to present the way we interpret the evolution of the population in the chemostat. We want to impose to our model the fact that the rate of production has to be proportional to the existing population and to the amount of available resources. Hence a logistic model of the population, where c denotes the concentration of cells in the medium: | ||
Revision as of 10:31, 29 August 2008
|
BOB (Based On Bibliography) Approach
IntroductionThe key problem with a dynamic system consists in the fact that adding a new equation gives a more detailed idea of the overall process, but one looses meaning by doing so since new undefined parameters appear. Hence, it becomes hard to link those parameters with a biological meaning and reality. In that respect we chose to build at first a simplified model, which would enable us to help us understand the processes implied in the system. In that respect, we chose not to introduce the mRNA state between transcription and translation in our model. We presented things as if a protein would act directly upon the following. Furthermore, we assumed that describing routinely every step, would only force us into finding more parameters. This preliminary approach is mainly based on a bibliographical work. In fact, it is important to understand that with this approach, we did not intend to design the most accurate model possible. We found essential to choose only parameters that we could determine or control in the wet lab. The main goal was to get quickly a first idea of the way our system could behave. The goal here is to present the differential equations we used in the model. At each step we shall describe why we chose these precise equations, the drawbacks and possible improvements, the parameters involved and eventually a biologically coherent value. Model
Steps of the ModelWe chose to broke up this system in three sub systems for presentation clarity
see also Synchronisation module
Population evolution
FIFO Temporal Order ModuleSteps involved
Mathematical model
DiscussionNormalization
If we set [fliA] = 1 and [flhDC] = 1, and we solve, we obtain : Setting the equilibrium value to 1 corresponds to setting
With an input of flhDC equal to 1, the solution of the differential equation is: And the condition on the equilibrium imposes
Which gene goes were?
Synchronisation ModuleSteps involved
Mathematical ModelDynamics of HSLFirst and foremost, HSL is the key element in the synchronisation process: we used a diffusive specie in order to balance a value between cells. Thus, the HSL concentration denoted [HSL] become this "shared" value, the outside medium concentration denoted [HSLext] being an intermediate value. We use the classical osmosis term η x ( [HSL] - [HSLext] ) where η = membrane permeability x ( area 1cell / volume 1cell ) is the diffusion rate expressed in time-1. The degradation rate is linear: - γ x [HSL]. To model the production, we were at first inspired by [2] where it is described as being linear: β x [LasI] where β is a given constant value. However, the results presented in this study were introduced as only being theoretical so we chose to model the creation of HSL by a Michaelis Menten expression (because there is no known cooperativity). The final expression where ΘHSL is expressed in concentrations unit and βHSL in (concentration * time) unit is:It is important to note that we took into account the fact that lasR/(lasR linked to HSL) was a function of HSL. However, we assumed that the fraction of HSL bound to lasR would not influence HSL concentration; this is the reason why, no “degradation due to binding" term appears in the HSL model. Dynamics of HSLextThe evolution of HSLext may be described with three terms. First of all, there is a dilution rate, Drenewal, due to the renewal of the chemostat. There is the usual degradation rate,γ[HSL]ext ). Which gives where TetR=f(HSL)
Oscillations ModuleFlhDC = f(TetR) For this last step, since we have not found any article indicating that we could simplify the model by using a linear function. Then, we chose a complete Hill function to describe the dynamics of flhDC: Parameters summaryParameters Table(Under Construction)
Remarks
The value for half-life time we found and used is 35min.
BibliographyMuch of our inspiration comes from four articles to which we shall refer in the next subsections :
A VOIR
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 "
"