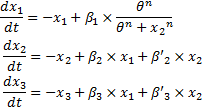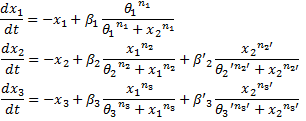Team:Paris/Modeling/BOB/Akaike
From 2008.igem.org
(Difference between revisions)
(→Experiment) |
(→Experiment) |
||
| Line 22: | Line 22: | ||
* We made a set of data out of a noised Hill function. In fact, our data set was made by using the same equations as System#2, but we introduced a normal noise for each point. Thus, System#1 is penalized because its RSS will be greater than that of System#2. Nevertheless, System#2 will be more penalized by its number of parameters. | * We made a set of data out of a noised Hill function. In fact, our data set was made by using the same equations as System#2, but we introduced a normal noise for each point. Thus, System#1 is penalized because its RSS will be greater than that of System#2. Nevertheless, System#2 will be more penalized by its number of parameters. | ||
* With Matlab, we run a fitting simulation for each system, and we obtained the RSS. We then evaluated the different criteria for both models. The results are presented below. | * With Matlab, we run a fitting simulation for each system, and we obtained the RSS. We then evaluated the different criteria for both models. The results are presented below. | ||
| + | <center> | ||
{| | {| | ||
|- style="background: #649CD7;" | |- style="background: #649CD7;" | ||
| Line 44: | Line 45: | ||
| | | | ||
|} | |} | ||
| - | + | </center> | |
Revision as of 13:08, 3 September 2008
|
(Under Construction) Model Comparison
Short introduction to the criteria
where n denotes the number of experimental values, k the number of parameters and RSS the residual sum of squares. The best fitting model is the one for which those criteria are minimized.
Experiment
System#1 : using the linear equations from our BOB approach : System#2 : using classical Hill functions :
We mostly used the definition of the criteria given in : [http://www.liebertonline.com/doi/pdf/10.1089/rej.2006.9.324 K. Kikkawa.Statistical issue of regression analysis on development of an age predictive equation. Rejuvenation research, Volume 9, n°2, 2006.] |
|||||||||||||||
 "
"