From 2008.igem.org
(Difference between revisions)
|
|
| Line 9: |
Line 9: |
| | | | |
| | <!--Autoinducer --> | | <!--Autoinducer --> |
| - | To archieve synchronization we use QS. | + | * To archieve synchronization we use QS. |
| - | | + | |
| | | | |
| | == Kinetics == | | == Kinetics == |
Revision as of 21:05, 25 October 2008
|
Model Construction
Description
- First of all, it seems important at this stage to present the way we interpret the evolution of the population in the chemostat. We want to impose to our model the fact that the rate of production has to be proportional to the existing population and to the amount of available resources.
- We choose a logistic model
- To archieve synchronization we use QS.
Kinetics
- Hence a logistic model of the population, where c denotes the concentration of cells in the medium:
- Then, we need to add the death term, and a dilution term cause by the renewal of the chemostat. Finally we get :
where cmax is the carrying capacity for cell growth, and
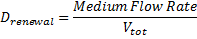 the dilution rate, d the death rate constant
Parameters Search
manly from literature but also from S0 analysis.
| Parameters
|
|
|
| Chemostat
| Parameter
| Meaning
| Original Value
| Normalized Value
| Unit
| Source
|
| figure / equations of Chemostat
| αcell
| Growth rate
| 0.0198
| 1
| min-1
| wet-lab
|
| cmax
| Carrying capacity for cell growth
| 0.1
| 0.1
| µm3
| [3]
|
| Drenewal
| Dilution rate
| 0.00198
| 0.1
| min-1
| wet-lab ([3])
|
| d
| Death rate
| 0.0099
| 0.5
| min-1
| wet-lab
|
|
|
| Quorum Sensing
| Parameter
| Meaning
| Original Value
| Normalized Value
| Unit
| Source
|
| figure / equations of Quorum Sensing
| γHSL
| Degradation rate
| 0.0053
| 0.2690
| min-1
| wet-lab
|
γHSLext
| Degradation rate
| 0.0106
| 0.5380
| min-1
| [6]
|
| βHSL
| Production rate
| 0.3168
| 16
| min-1
| ∅
|
| η
| Diffusion rate
| 10
| 505
| min-1
| [2]
|
| nHSL
| Hill coefficient
|
| 4
|
| [3]
|
| θHSL
| Hill characteristic concentration for the second operator
|
| 0.5
| c.u
| [3]
|
|
"
