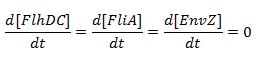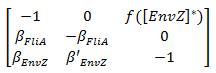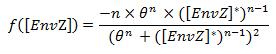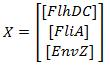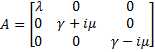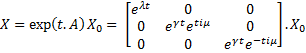Team:Paris/Network analysis and design/Core system/Mathematical analysis and simulations/Mathematical analysis
From 2008.igem.org
(→Navigator) |
(→Navigator) |
||
| Line 75: | Line 75: | ||
| - | <center>[[Team:Paris/Network_analysis_and_design/Core_system|Back to the overall presentation of our system and model]]</center> | + | <center>[[Team:Paris/Network_analysis_and_design/Core_system|Back to the overall presentation of our system and model]]</center> |
| + | <center>[[Team:Paris/Network_analysis_and_design/Core_system/Mathematical_analysis_and_simulations|Back to the Mathematical analysis and simulations section]]</center> | ||
<center>[[Team:Paris/Network_analysis_and_design/Core_system/Mathematical_analysis_and_simulations/Mathematical_analysis#Understanding_the_dynamics|Top of the page]]</center> | <center>[[Team:Paris/Network_analysis_and_design/Core_system/Mathematical_analysis_and_simulations/Mathematical_analysis#Understanding_the_dynamics|Top of the page]]</center> | ||
Revision as of 13:02, 26 October 2008
|
Mathematical analysis
Understanding the dynamics
The classical approach consists in finding the equilibrium state, by setting Then, we evaluate the jacobian matrix, so as to put the system under its linearized form:
which gives : Then, we want to find the eigenvalues of the jacobian matrix, because they make us understand the behavior of the system. Here is the theoretical explanation : The λ and γ coefficients make the convergence. In our case they are negative terms, which explains the fact that we have a quick convergence for the system. Ideally, it could be convenient to find which parameter influence this coefficient, so as to play with it and be able to propose a better control of the convergence.
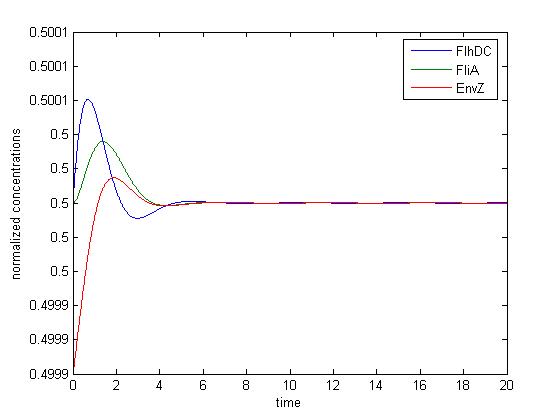
We obtained three solutions : -0.2382 - 0.6139i -0.2382 + 0.6139i 0.4764 We are only interested in positive real solutions. We can note that 0.4764 corresponds well to the experimental equilibrium value. Then we evaluated the eigenvalues for the jacobian : -1.0159 + 0.5042i -1.0159 - 0.5042i -0.1111 We can note that the λ and γ coefficient are negative, which corroborates the fact that we obtain a convergence. Finally for since μ=0.5042 we find a theoretical period of Ttheoretical=12.4617. Experimentally, we find Texperimental~10. We can see that some numerical noise must be involved, which gives the reading of the period quite tough. However, we get the same order of magnitude, which proves that the oscillations are occuring, though quietly!
Furthermore, this theoretical study helps us understand that reducing the attenuation is tough. In fact, whatever the base in which you consider a matrix, the trace is conserved. Here, we obtain : Since λ and γ are assumed (thanks to simulations) to be negative, we cannot avoid to have their sum to be (with absolute value) superior to 2. The only chance we have would be that the weight goes in the λ parameter because this parameter plays a role in the third dimension, in which we are not interested. However, for every simulation we made, we found the opposite. Trying to evaluate with non-numerical calculus does not provide relevant material. However, we now know that βFliA influences the attenuation. We ran a simulation with βFliA=0.02 This confirms what we saw previously. In this second case, the system is therefore less attenuated, and some very tiny damped oscillations can be observed. Last but not least, one should not forget that we chose a normalized interpretation of the system. Thus, even though the attenuation phenomenon remains unchanged, the tiny oscillations we see may indeed be observable. |
 "
"