Team:ETH Zurich/Modeling/Genome-Scale Model
From 2008.igem.org
Luca.Gerosa (Talk | contribs) (→Genome Scale Models, FBA and E.Coli K12 MG1655) |
Luca.Gerosa (Talk | contribs) (→Genome Scale Models, FBA and E.Coli K12 MG1655) |
||
| Line 42: | Line 42: | ||
{| border="1" align="center" | {| border="1" align="center" | ||
|- | |- | ||
| - | |[[ | + | |[[|center|200px|]]<br> |
<div style="text-align:center;">'''Central Metabolism'''</div> | <div style="text-align:center;">'''Central Metabolism'''</div> | ||
|[[Image:Amino acid.jpg|center|200px|]]<br> | |[[Image:Amino acid.jpg|center|200px|]]<br> | ||
<div style="text-align:center;">'''Amino Acid Metabolism'''</div> | <div style="text-align:center;">'''Amino Acid Metabolism'''</div> | ||
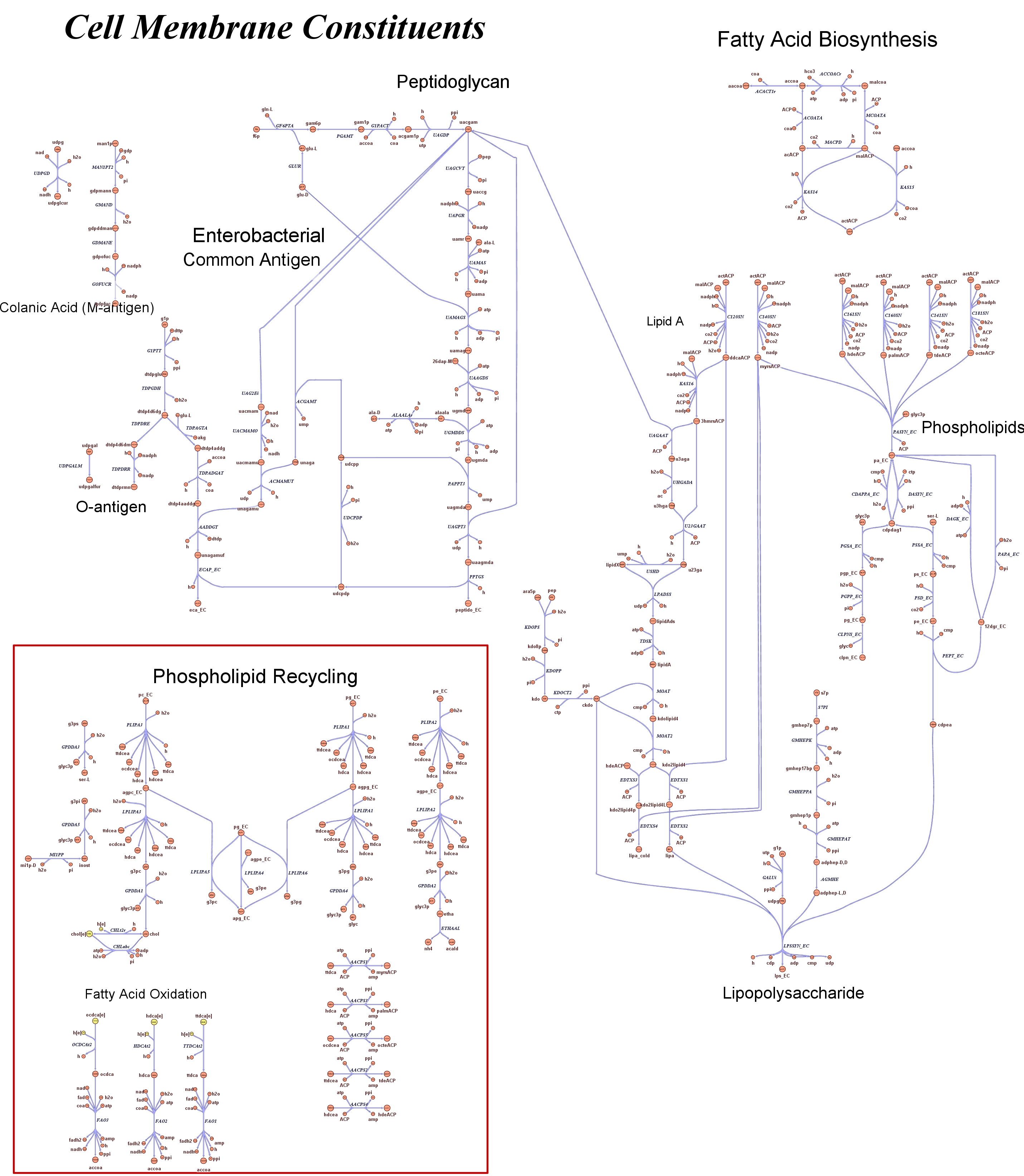
| - | |[[Image: | + | |[[Image:Cell membrane.jpg|center|200px|]]<br> |
<div style="text-align:center;">'''Cell Membrane'''</div> | <div style="text-align:center;">'''Cell Membrane'''</div> | ||
|- | |- | ||
| Line 53: | Line 53: | ||
|[[Image:ChemostatSmallIntro.jpg|center|200px|]]<br> | |[[Image:ChemostatSmallIntro.jpg|center|200px|]]<br> | ||
<div style="text-align:center;">'''Nucleotide Metabolism'''</div> | <div style="text-align:center;">'''Nucleotide Metabolism'''</div> | ||
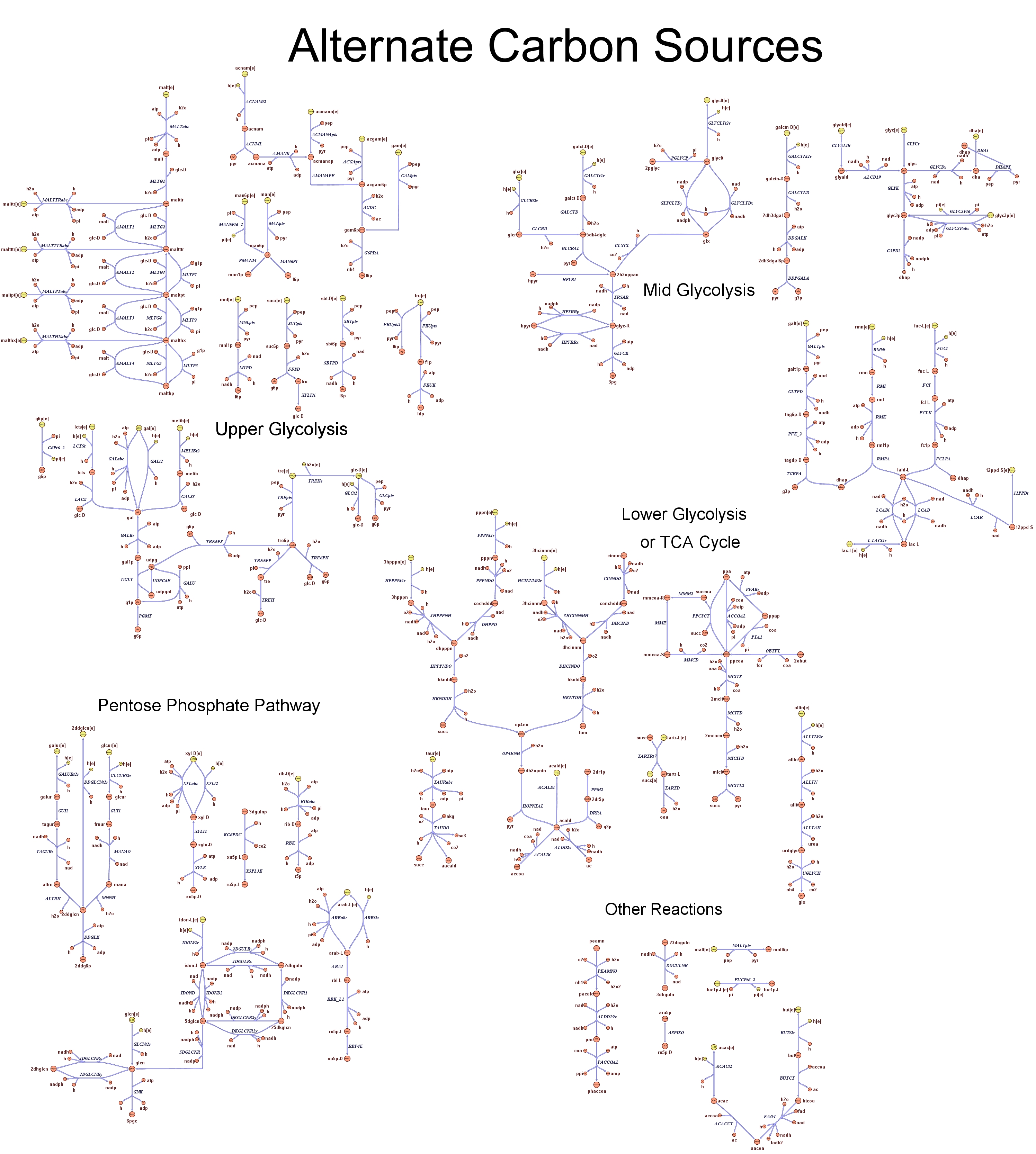
| - | |[[Image: | + | |[[Image:Alternate carbon.jpg|center|200px|]]<br> |
<div style="text-align:center;">'''Alternative Carbon Sources'''</div> | <div style="text-align:center;">'''Alternative Carbon Sources'''</div> | ||
|} | |} | ||
Revision as of 16:17, 26 October 2008
Genome Scale AnalysisIn the Restriction Enzymes Analysis modeling section we deal with the analysis of restriction enzymes effects on the genome from the simple point of view of nucleotide sequences and cutting patterns. This is not informative enough when we try to understand if the key principles of reduction and selection at the base of our minimal genome approach are valid in the context of the whole cell response. It is evident that our selection method for smaller genome size strains is based on the assumption that is possible to control growth rate as a function of its genome size. As explained in the Project Overview, we put a selective pressure on the genome size by combining two effects together: the random reduction of the genome size by restriction enzymes cutting and the feeding of a limited amount of thymidine nucleotides on the background of a thymidine auxotrophic strain. In this context, one should also consider the effects that the lost of chromosomal coding regions may have on the physiology of the cell. This scenario needs to be validate using modeling techniques that relate genome content and substrates avaiability with cell physiology, on a system level fashion. Fortunately, in the last ten year huge progress have been achieved in coding our understanding of biological networks into whole cell comprehensive stochiometric models. This model typology is called genome scale modeling and we use the most update genome scale model for our working strain (E.Coli K12 MG1655) in order to answer the following questions:
These questions are answered below, in the respective sections. As first we introduce the genome scale model concepts, the Flux Balance Analysis theory and in particular the iAF1260 E.Coli Genome Scale Model developed by [http://gcrg.ucsd.edu/|the Palsson's Group at UCSD], that we modified and used. In the following sections we show the results of simulations for the different questions to be answered. Genome Scale Models, FBA and E.Coli K12 MG1655Genome scale models are biological network reconstructions that effectively mape genome annotations (ORFs) to biochemical reactions that define the metabolic network specific to a particular organism. They are also called stoichiometric models because encode calculation of quantitative relationships of the reactants and products in the balanced biochemical reactions in the organism. When they are enough informative to cover a consistent part of the known organism functions are called in-silico organisms, bacause it is possible to use them as models to simulate whole cell system responses. Genome scale models are used in combination with Flux Balance Analysis in order to predict the physiology (growth rate, uptake rates, yields etc..) of the in-silico organism depending on variable external nutrient conditions or changes in genome composition (in-silico knockout experiments). In the last decade this modelling technique has proved to give consistent results with experimental data under various hetereogeneous conditions of testing (4). Mathematically, Flux Balance Analysis uses the stoichiometric information in order to predict the metabolic flux distribution under the assumption of maximization of a particular cell process (for example maximizing biomass production). If N is the stochiometric matrix, and V the vector of fluxes, Flux Balance Analysis assumes steady state: And then compute a flux solution according to a maximization (or the correspective minimization) function: Once the metabolic fluxes are known, is possible to calculate physiology parameters. For a complete introduction to these concepts please read this [http://www.nature.com/nbt/web_extras/supp_info/nbt0201_125/info_frame.html| Genome Scale Models introduction]. Focusing on the organism of our interest, the E. coli in silico organims we use is iAF1260 and includes the genes involved in central metabolism, amino acid metabolism, nucleotide metabolism, fatty acid and lipid metabolism, carbohydrate assimilation, vitamin and cofactor biosynthesis, energy and redox generation, and macromolecule production (i.e. peptidoglycan, glycogen, RNA, and DNA). In order to give a flavour about the pathways included in the model we post the graphical representation of reactions and metabolits that has been produced for the previous model version (4).
Thymidine limitation effects on growth ratesGenome size effects on growth ratesDifferent mediumsGrowth rates as output of whole cell system behaviourComparing different approaches to minimal genomeReferences(1) "Thirteen Years of Building Constraint-Based In Silico Models of Escherichia coli" ,Jennifer L. Reed and Bernhard Ø. Palsson, Journal of Bacteriology, May 2003, p. 2692-2699, Vol. 185, No. 9 |
 "
"