Introduction
- The key problem with a dynamic system consists in the fact that adding a new equation gives a more detailed idea of the overall process, but one looses meaning by doing so since new undefined parameters appear. Hence, it becomes hard to link those parameters with a biological meaning and reality.
- In that respect we chose to build at first a simplified model, which would enable us to help us understand the processes implied in the system. In that respect, we chose not to introduce the mRNA state between transcription and translation in our model. We presented things as if a protein would act directly upon the following. Furthermore, we assumed that describing routinely every step, would only force us into finding more parameters.
- This preliminary approach is mainly based on a bibliographical work. In fact, it is important to understand that with this approach, we did not intend to design the most accurate model possible. We found essential to choose only parameters that we could determine or control in the wet lab. The main goal was to get quickly a first idea of the way our system could behave.
- The goal here is to present the differential equations we used in the model. At each step we shall describe why we chose these precise equations, the drawbacks and possible improvements, the parameters involved and eventually a biologically coherent value.
Bibliography
Much of our inspiration comes from four articles to which we shall refer in the next subsections :
- [1] Shiraz Kalir, Uri Alon. Using quantitative blueprint to reprogram the dynamics of the flagella network. Cell, June 11, 2004, Vol.117, 713-720.
- [2]Jordi Garcia-Ojalvo, Michael B. Elowitz, Steven H. Strogratz. Modeling a synthetic multicellular clock : repressilators coupled by quorum sensing. PNAS, July 27, 2004, Vol. 101, no. 30.
- [3]Nitzan Rosenfeld, Uri Alon. Response delays and the structure of transcription networks. JMB, 2003, 329, 645-654.
- [4]Nitzan Rosenfeld, Michael B. Elowitz, Uri Alon. Negative autoregulation speeds the response times of transcription networks. JMB, 2003, 323, 785-793.
- [5]S.Kalir, J. McClure, K. Pabbaraju, C. Southward, M. Ronen, S. Leibler, M. G. Surette, U. Alon. Ordering genes in a flagella pathway by analysis of expression kinetics from living bacteria. Science, June 2001, Vol 292.
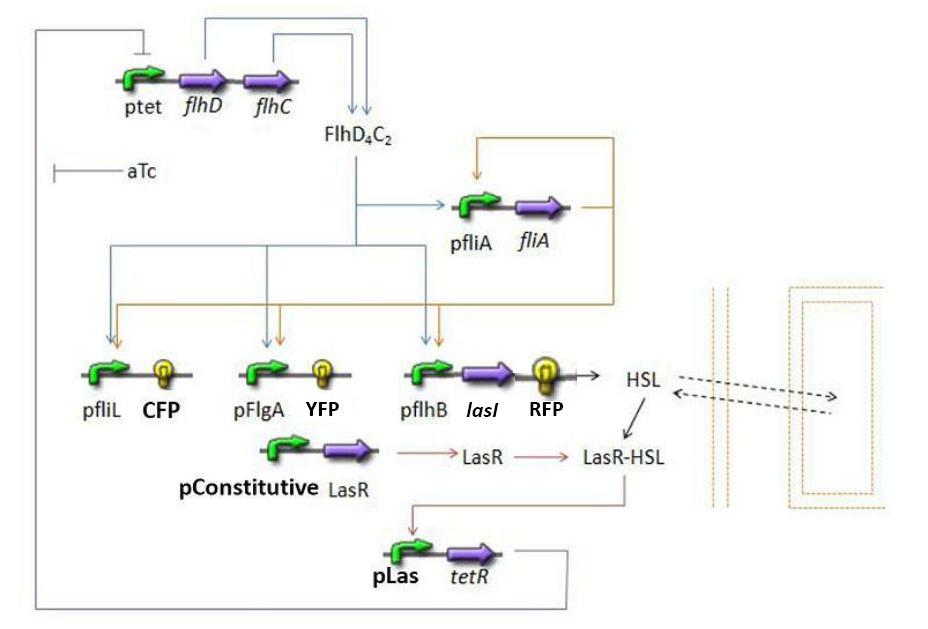
Summary of the steps modeled
Here is a quick summary of the step we decided to interpret mathematically...
- FIFO temporal order system
- FliA behind pFliA= f(FlhDC,FliA)
- CFP behind pFliL = f(FlhDC,FliA)
- YFP behind pFliL = f(FlhDC,FliA)
- RFP and LasI behind pFliL = f(FlhDC,FliA)
- Synchronisation : las system
- HSL = f(LasI)
- HSL ⇋ HSLext
- TetR = f(HSL)
- FlhDC = f(TetR)
- Synchronisation : lux system
- HSL = f(LasI)
- HSL ⇋ HSLext
- TetR = f(HSL)
- FlhDC = f(TetR)
Establishing the model
Population evolution
First of all, it seems important at this stage to present the way we interpret the evolution of the population in the chemostat. We want to impose to our model the fact that the rate of production has to be proportional to the existing population and to the amount of available resources. Hence a logistic model of the population, where c denotes the concentration of cells in the medium:
Then, we need to add the death term, and a dilution term cause by the renewal of the chemostat. Finally we get :
FIFO temporal order Module
(lien partie model)
Steps involved
Mathematical model
Discussion
Normalization
Which gene goes were?
Simulations and Results
Synchronization Module : las System
(lien partie model)
Steps involved
Mathematical Model
Dynamics of HSL
Dynamics of HSLext
TetR=f(HSL)
FlhDC=f(TetR)
Simulations and results
Parameters summary
Testing the oscillations
Testing the FIFO
Testing the Synchronization
|
 "
"