|
Model Construction
Description
- We chose to use a chemostat. We want to impose to our model the fact that the rate of production has to be proportional to the existing population and to the amount of available resources.
- We assume a logistic model for the population kinetics in the chemostat (reference).
- To archieve synchronization we use QS. Explain the principle?
Kinetics
- The concentration variation of cells in the chemostat over time can be expressed in terms of a production (positive) term and degradation (negative) terms:
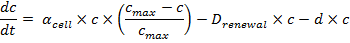 , ,
For the production term, we use a logistic equation to model cell growth, according to standard assumptions [Garcia-Ojalvor--ref]. The behaiviour obtained is the following one: at low population density, the concentration of cells in the chemostat (c) increase exponentialy with a growth rate αcell and at high population density, the population reaches a maximum concentration, cmax.
For the degradation term, it is considered that c decrease proportionaly to both a dilution phenomena cause by the renewal of the chemostat (Drenewal) and cell death (d).
- To model the quorum sensing dynamics, we consider the production of HSL as:
eqHSL 1,
the transport of HSL is given by:
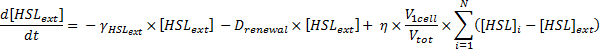 , ,
where...
when in...:
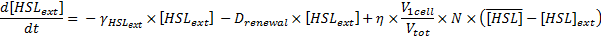 , where , where 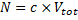 ; ;
and the activation of envZ depends of the concentration of HSL according to:
eqHSL 3.
Parameters Search
manly from literature but also from S0 analysis.
| Parameters
|
|
|
| Chemostat
| Parameter
| Meaning
| Original Value
| Normalized Value
| Unit
| Source
|
| figure / equations of Chemostat
| αcell
| Growth rate
| 0.0198
| 1
| min-1
| wet-lab
|
| cmax
| Carrying capacity for cell growth
| 0.1
| 0.1
| µm3
| [3]
|
| Drenewal
| Dilution rate
| 0.00198
| 0.1
| min-1
| wet-lab ([3])
|
| d
| Death rate
| 0.0099
| 0.5
| min-1
| wet-lab
|
|
|
| Quorum Sensing
| Parameter
| Meaning
| Original Value
| Normalized Value
| Unit
| Source
|
| figure / equations of Quorum Sensing
| γHSL
| Degradation rate
| 0.0053
| 0.2690
| min-1
| wet-lab
|
γHSLext
| Degradation rate
| 0.0106
| 0.5380
| min-1
| [6]
|
| βHSL
| Production rate
| 0.3168
| 16
| min-1
| ∅
|
| η
| Diffusion rate
| 10
| 505
| min-1
| [2]
|
| nHSL
| Hill coefficient
|
| 4
|
| [3]
|
| θHSL
| Hill characteristic concentration for the second operator
|
| 0.5
| c.u
| [3]
|
|
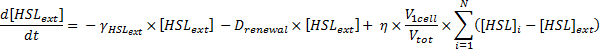 ,
, "
"
