Team:Paris/Modeling/f3bis
From 2008.igem.org
At the steady-state, we haveand
so the expression
gives
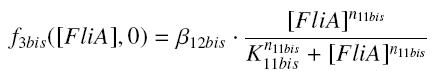
and
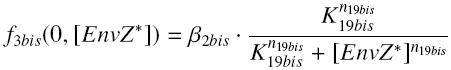
and for calculated values of the TF,
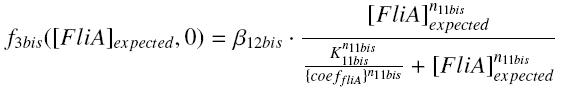
and
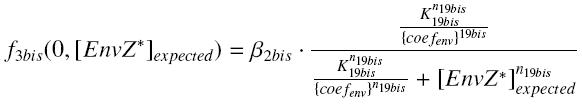
| param | signification | unit | value |
| [expr(pFlhDC)] | expression rate of pFlhDC with RBS E0032 | nM.s-1 | see "findparam" need for 20 + 20 measures and 5x5 measures for the SUM? |
| γGFP | dilution-degradation rate of GFP(mut3b) | s-1 | ln(2)/3600 |
| [GFP] | GFP concentration at steady-state | nM | need for 20 + 20 measures and 5x5 measures for the SUM? |
| (fluorescence) | value of the observed fluorescence | au | need for 20 + 20 measures and 5x5 measures for the SUM? |
| conversion | conversion ration between fluorescence and concentration | nM.au-1 | (1/79.429) |
| param | signification corresponding parameters in the equations | unit | value |
| β12 | production rate of FliA-pFlhDC with RBS E0032 β12 | nM.s-1 | |
| (K11/{coeffliA}n11) | activation constant of FliA-pFlhDC K11 | nMn11 | |
| n11 | complexation order of FliA-pFlhDC n11 | no dimension | |
| β2 | production rate of OmpR-pFlhDC with RBS E0032 β2 | nM.s-1 | |
| (K19/{coefompR}n19) | activation constant of OmpR-pFlhDC K19 | nMn19 | |
| n19 | complexation order of OmpR-pFlhDC n19 | no dimension |
Then, if we have time, we want to verify the expected relation
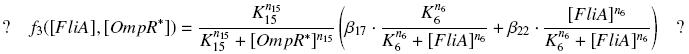
 "
"