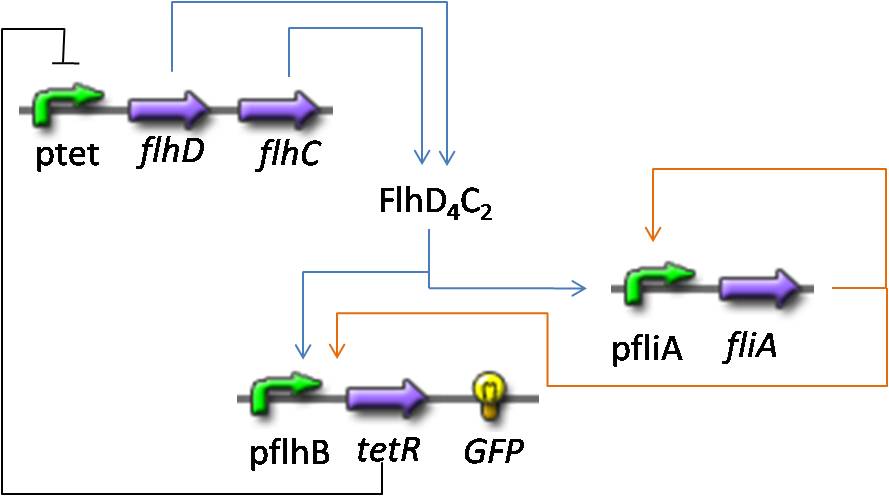
|
(Under Construction : synchronisation and whole system)
Simulations and Mathematical analysis
Oscillations
Short System
- We wanted to see if, from a mathematical point of view, it was possible for the "short" system presented above to hover.
- Here are the equations we took into account :
- The equations are normalized (thus the degradation term set to 1), as well as the parameters :
| Parameters Used
|
| Parameter
| Normalized Value
|
| βFlhDC
| 1
|
| θFlhDC
| 0.4545
|
| n
| 2
|
| βFliA
| 0.1429
|
| β'FliA
| 0.8581
|
| βLasI
| 0.2222
|
| β'LasI
| 0.7778
|
- As introcued before, the goal of this model was to give us useful bases on which to work on. Then, we shall use the values of the parameters presented below as a "starting point". Again, we shall present a double approach, composed of a theoretical and a simulation approach. Both approaches should interact so as to help us understand the way our system behaves.
Observations
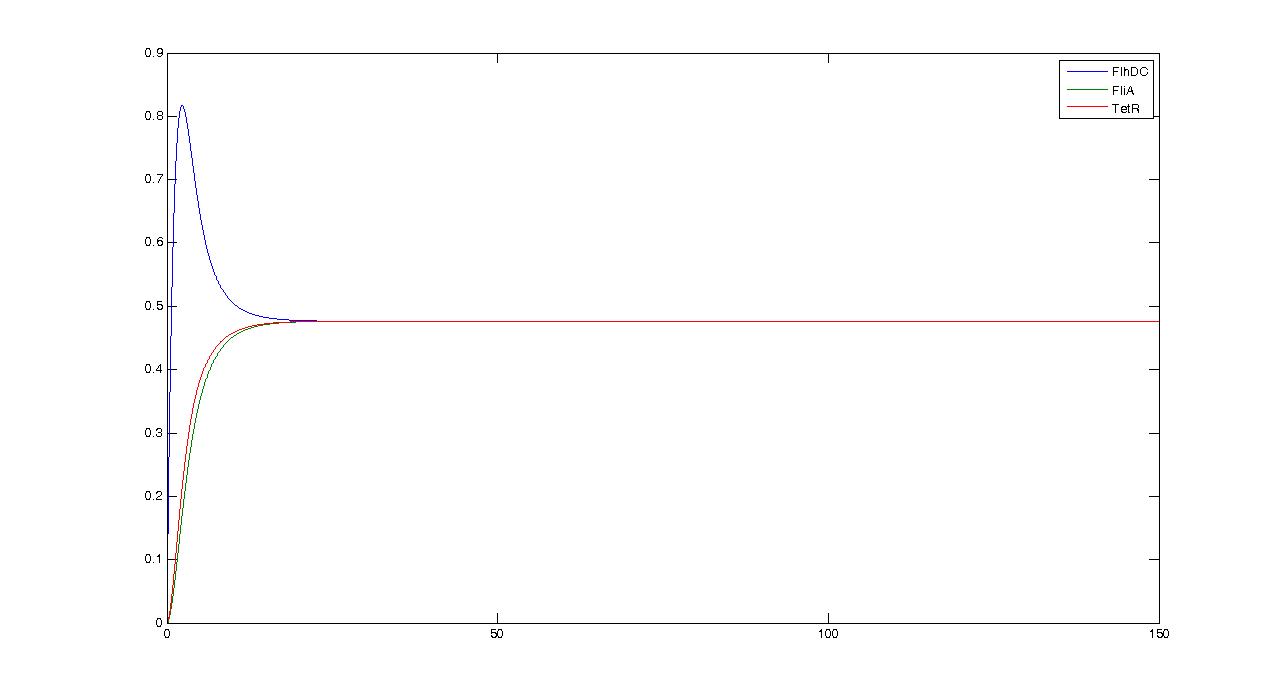
- First of all, let us see what the simulation gives, and what pieces of information we can get from it.
By looking at this simulation, we could think that it is going to be hard to get oscillations...
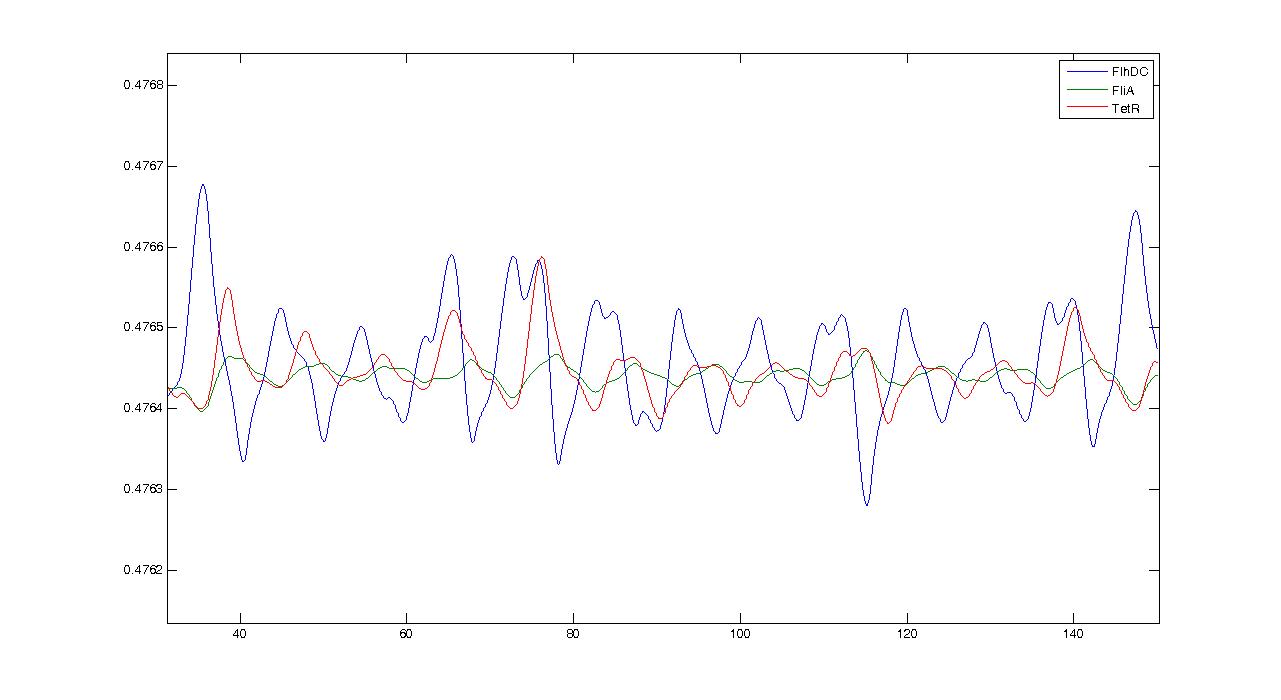
However when we zoom, we get this more reassuring view :
Understanding the dynamics
Using these elements to improve the system and give directions to the wet-lab
|
 "
"