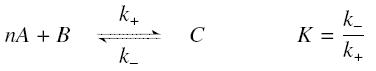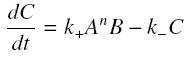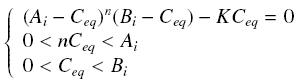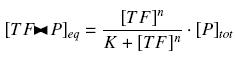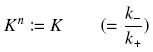Complexations Caracterisation
The first hypothesis is that a complexation reaction is fully determined by the following :
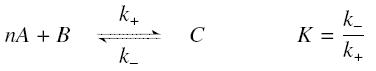
and that the rates k+ et k- stay constant under all conditions. Then, the second hypothesis is that these equations are (kinetically speaking) elementary :
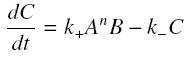 and at steady-state :
and at steady-state : 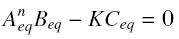
Then, since we guess that the only datas we will have are the quantities of A and B introduced (Ai and Bi), the only equations we will deal with is the following, entirely determining the concentration Ceq at steady-state (at least if we take the smallest real root of the equation, it is useless to demonstrate the unicity, or even the existence, of such a solution) :
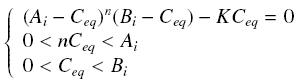
Equilibrium of a Complex
Hill Functions
The previous system of complexation applied in particular to the association of the Promoters (P) and its Transcription Factor (TF).
Because the promoters on a "low copy plasmid" exists in the cell in ten exemplaries, in contrary to a protein, which, as long as it is produced (even weakly) exists in thousands of exemplaries, we assume can the quantities of TF and P are different by several orders of magnitude. Then, with the previous notations, if A, B and C stands respectively for TF, P and the complex TF><P, we will get
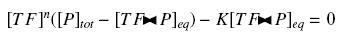
that we can easily solve with :
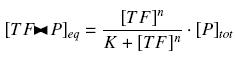
Depending to the order n (also called cooperativity, because it correponds to the possibilities of the transcription factor to binds in a group on the promoter), this function is a sigmoïd, known as the Hill function. The parameter K , called activation constant, is often replaced in the previous expression by the following notation
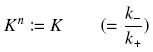
It simplifies the manipulations of the expression ; we can notice that K represents now the amount of TF needed to bind half of the total P in the cell.

Finding Parameters
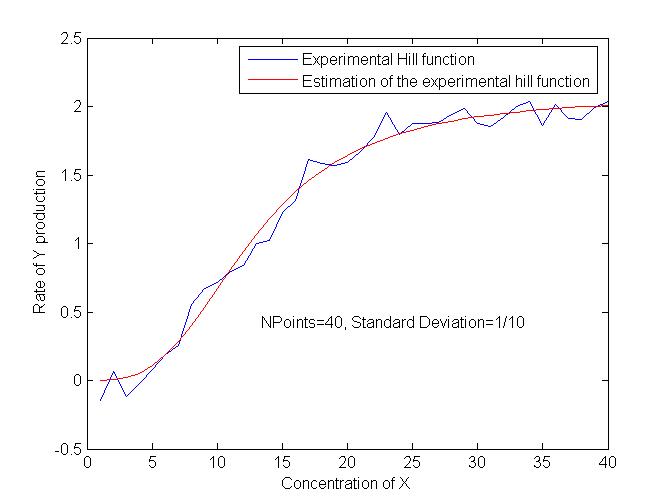
Then, by solving the complexation equation for a given set of K et n (and, in term of production of protein, the b (or β) parameter (see hypothesis)), we can have an approximation of the corresponding Ceq. The idea, in order to find the bests parameters which correspond to our measurements, is to run a basical program of quadratic optimisation. The final error would tell us if our modelisation is consistent.
((((the following is not coresponding to the new model, but we will use the same frame to expose the corresponding program)))))
(((((((This program aims at fill this data bank, from experimental data obtained by our wet lab. )))))))
(((((( After some trials, we have obtained interesting results in terms of precision. We are now trying to test the robustness of the estimations in order to quantify the influence of biological variance in the results as well as the influence of the number of points available. ))))))))
((((( )))))
(((((( The corresponding code can be found there : Estimation of the parameters )))))))
|  "
"