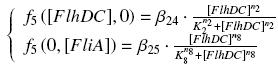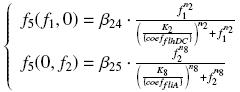Team:Paris/Modeling/More From2Ode Expl
From 2008.igem.org
|
All Biological Assumptions
Return to "from molecular reaction to Non-Linear ODEs"
Polymere of Transcription FactorAs it is explained in the introduction for the case of "FlhDC", instead of considering every polymere and complexes of proteins, we simplify those phenomenon by dealing with "abstract" proteins which represents the real transcription factors. It is the case for :
It is actually an hexamere [?]
TetR dimerizes before acting on pTet [?]
aTC dimerizes before binding on TetR [?]
OmpR acts on pFlhDC only if phosphorylated (OmpR><P). If we use ompR*, mutated version of ompR, we consider that the phosphorylation is immediate. If we use envZ, we consider the "basal" presence of OmpR in the cell as an additional parameters, and we suppose that OmpR bound to EnvZ is immediately phosphorylated [?] TranscriptionWe suppose that the transcription rate is proportional to the amount of "effecive promoter" in the cell. An effective promoter is either a induced promoter bound to its transcription factor, either a free constitutive promoter. We use the following notations : Competition Between Transcription FactorsIf several transcription factors bind to a given promoter, those several complexations are in competition. To treat this phenomenon, we must know if a reaction is predominant, or if all the steady-states are reached "at the same time", oother rules of order. We made the following hypothesis :
Dilution/Degradation γAs we want the cells to remain in "exponential phase of growth", we assume that every protein involved in the system and for the characterisation has a half-life time far superior than the time of cell division. In that way, we consider that every protein in the cell disappears only by dilution, whose value would be estimated in the wet-lab. Translation : RBS issueWe use the GFPgenerator (E0240) in association with its RBS (B0032), to caracterise the "expression of the gene behind a given promoter". However, the Ribosome Binding Site of the gene influence it's expression. By considering that the translation rate depends near linearly of the Ribosome Binding Site (as we guess ; it gives the affinity between the mRNA and the ribosome !), we introduce a constant factor between the expected value of a protein and its real value. Moreover, we observe that at the steady state, the "disappearance rate" γ has got a linear effect on the concentration of the protein at equilibrium, too. For instance, if we consider a protein prot coded by its corresponding gene, put behind one of our "characterized promoters", with its natural RBS, we will have between our construction (expected value, given by GFP) and the real expression of prot the following relation It does not invalid our will of "systematic characterization", because this error is reported once prot is considered as transcription factor for the next step in which it is involved... ↓ why it is not a problem ? ↑
|
 "
"