Team:Paris/Modeling/Synchronisation
From 2008.igem.org
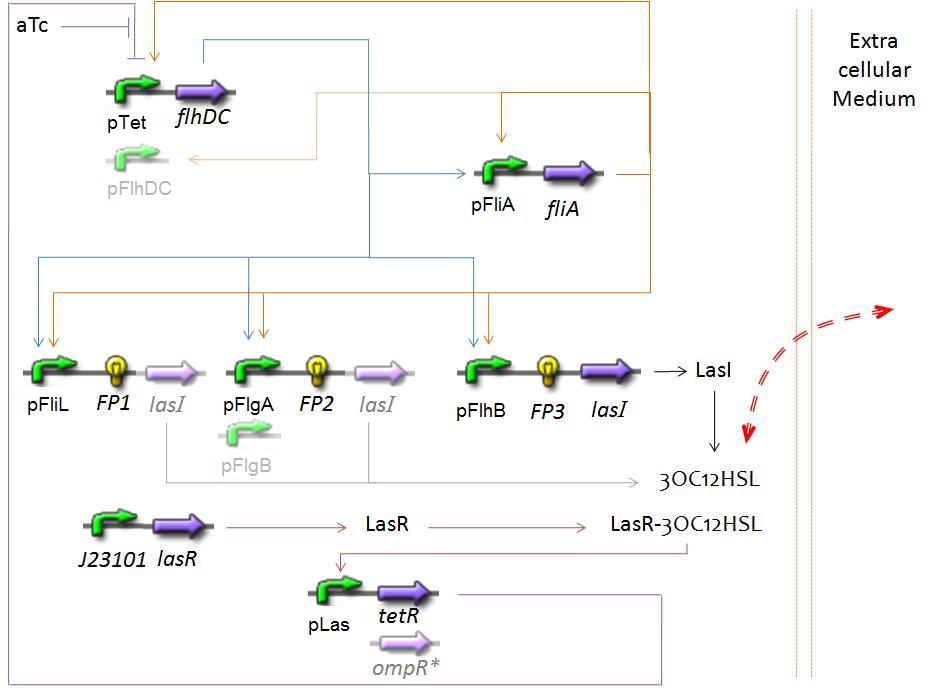
SynchronisationThe CircuitWe are know studying the following circuit, based on the one constituing the FIFO system, but with the mediation of AHL in the negative feed back loop. We will study three alternatives for the place of the lasI operon : on the first, second or third activated operon of the FIFO order. Biochemical Assumptionssee FIFO system We suppose a simple, passive diffusion through the cellular membrane, as it is described in the complexations considerations. Resulting EquationsFirst, we kept the equations of the FIFO system. We must ignore the equations specifics to the "direct" feed back loop, without using "quorum sensing" (very poorly colored in the document below). Then, we added at the end of the previous document the final equations (beginning page 14), regards to the complexations and diffusions. The red parameter (k73) is the only one we could never have by using our estimation plan, and we surely cannot find in the literature. We will then study the resulting behaviour for several ranges of this parameter, in order to deduce what is the needed of the feedback that allows to get oscillations (because this parameter gives the dynamic of a complexation, see the induction by diffusion of a small molecule in the final system.
|
Deterministic vs. Stochastic Model
First, we will simulate the resulting behaviour for only one cell. If this deterministic model leads to interesting oscillations, we will then simulate what happen for 10, 103, 106 (!), cells, to see if synchronisation is really effective. As the previous model is deterministic, we have to introduce differences between our cells. In this aim, we will use the standard deviation of our own measurements (see estimation of parameters) to give different parameters for each cell we introduce in our virtual medium...
 "
"