Team:Paris/Modeling/BOB/Simulations
From 2008.igem.org
(→Oscillations) |
(→Oscillations) |
||
| Line 46: | Line 46: | ||
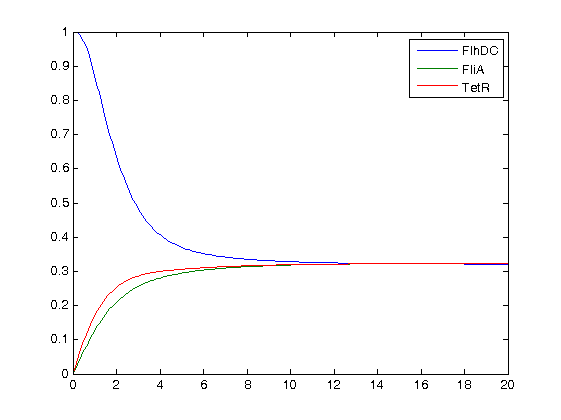
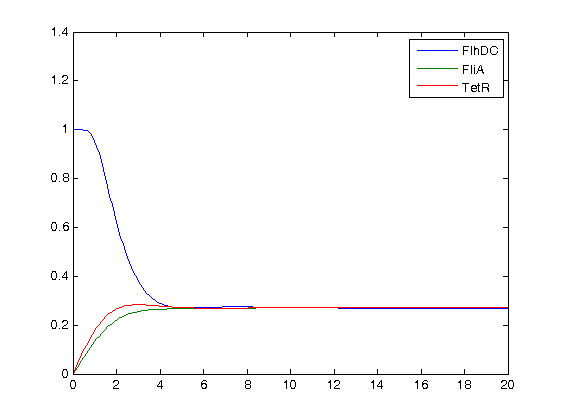
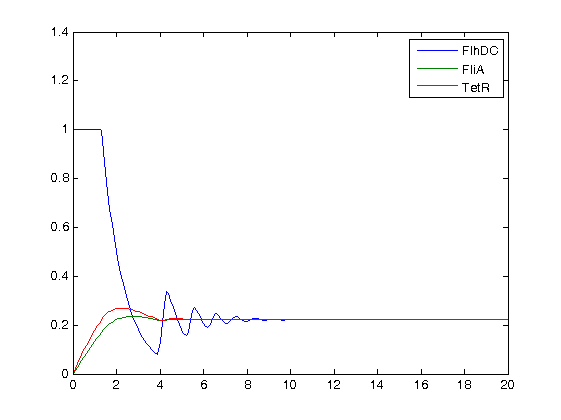
* At first, we quickly run simulations with different values of the parameters of the Hill function. Here are plot examples with pflhB at first : | * At first, we quickly run simulations with different values of the parameters of the Hill function. Here are plot examples with pflhB at first : | ||
| - | [[Image:essai_simul_2.jpg|300px|thumb|n=2 : no oscillations to be seen]] | + | [[Image:essai_simul_2.jpg|300px|center|thumb|n=2 : no oscillations to be seen]] |
| - | [[Image:essai_simul_n=5_2.jpg|300px|thumb|n=5 : some oscillations at the begining...]] | + | [[Image:essai_simul_n=5_2.jpg|300px|center|thumb|n=5 : some oscillations at the begining...]] |
| - | [[Image:essai_simul_n=5_zoom.jpg|300px|thumb| and some subdued oscillations when we zoom!]] | + | [[Image:essai_simul_n=5_zoom.jpg|300px|center|thumb| and some subdued oscillations when we zoom!]] |
| - | [[Image:essai_simul_n=300_2.jpg|300px|thumb|with a drastic (though non-biological) increase of n : n=300]] | + | [[Image:essai_simul_n=300_2.jpg|300px|center|thumb|with a drastic (though non-biological) increase of n : n=300]] |
* What consequences can we | * What consequences can we | ||
Revision as of 14:20, 2 September 2008
|
(Under Construction) Simulations and Mathematical analysis Oscillations
ccl : no oscill stable, mais un peu qd mme, donc a voir sur les constantes de temps mais intéressant: il faut choisir le premier, celui qui suit de plus pres flhDC!!! pour avoir le plus de chance d'avoir des oscillations, puisque c'est le terme de HIll qui fait osciller puis a voir avec le systeme bio perturbé, cad que c'est pas dramatique puis matrice puis biocham a introduire FIFO
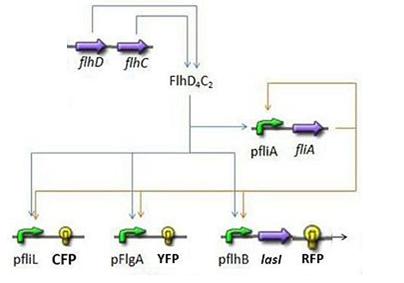
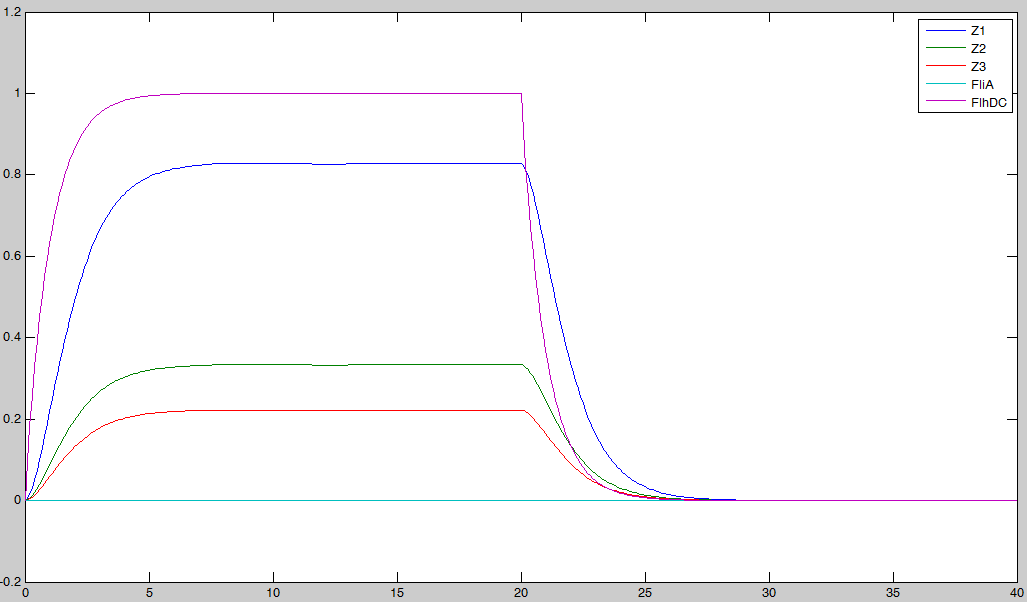
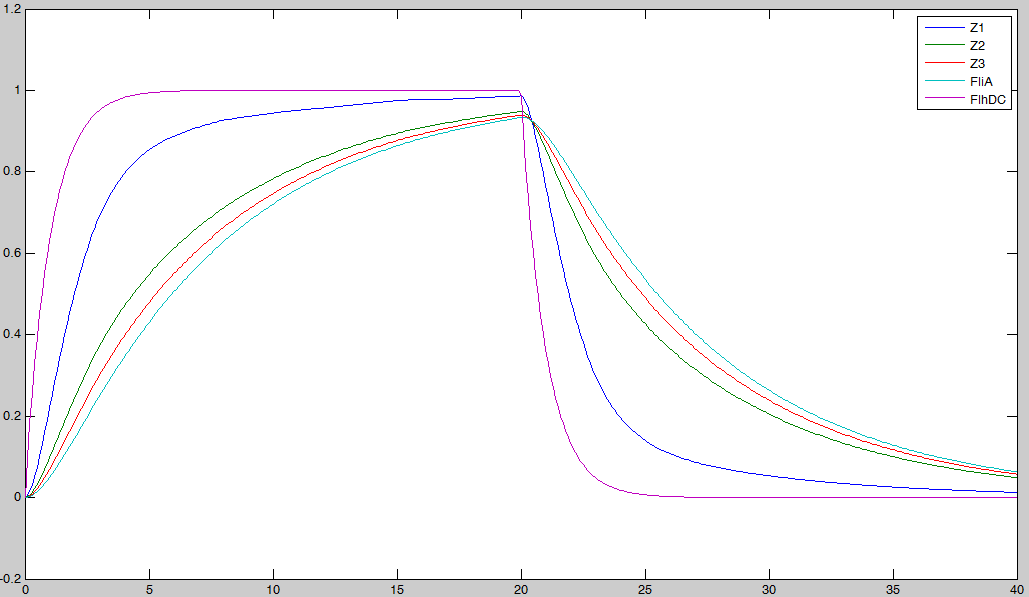
Here is the system we implementated using Matlab (see the corresponding codes) and the corresponding equations (for more detailed information see our establishment of the model). where CFP, YFP, and RFP will be denoted below as respectively Z1,Z2 and Z3.
In fact we assumed that this behavior for FlhDC was acceptable regarding its estimated behavior in the whole system.
We may see that there is a LIFO behavior rather than the FIFO we expect...
Synchronisation
|
||||||||||||||||||
 "
"