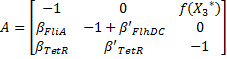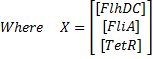Team:Paris/Modeling/BOB/Simulations page travail
From 2008.igem.org
(→Understanding the dynamics) |
(→Understanding the dynamics) |
||
| Line 65: | Line 65: | ||
Then, we evaluate the jacobian matrix, so as to put the system under its linearized form: | Then, we evaluate the jacobian matrix, so as to put the system under its linearized form: | ||
[[Image:Math3.jpg|center]] | [[Image:Math3.jpg|center]] | ||
| + | |||
[[Image:Math4.jpg|center]] | [[Image:Math4.jpg|center]] | ||
which gives : | which gives : | ||
| Line 70: | Line 71: | ||
[[Image:Math2.jpg|center]] | [[Image:Math2.jpg|center]] | ||
| - | Then, we want to find the eigenvalues of the jacobian matrix, because they make us understand the behavior of the system. For example (since it is the case for our system), let us assume that we gave one real eigenvalue, and two imaginary ones. | + | Then, we want to find the eigenvalues of the jacobian matrix, because they make us understand the behavior of the system. For example (since it is the case for our system), let us assume that we gave one real eigenvalue, and two imaginary ones. |
| + | |||
| + | expliqeur lexp de matrix puis donner le charpolu puis donner la période | ||
=== Using these elements to improve the system and give directions to the wet-lab === | === Using these elements to improve the system and give directions to the wet-lab === | ||
Revision as of 00:15, 7 October 2008
|
(Under Construction : synchronisation and whole system)
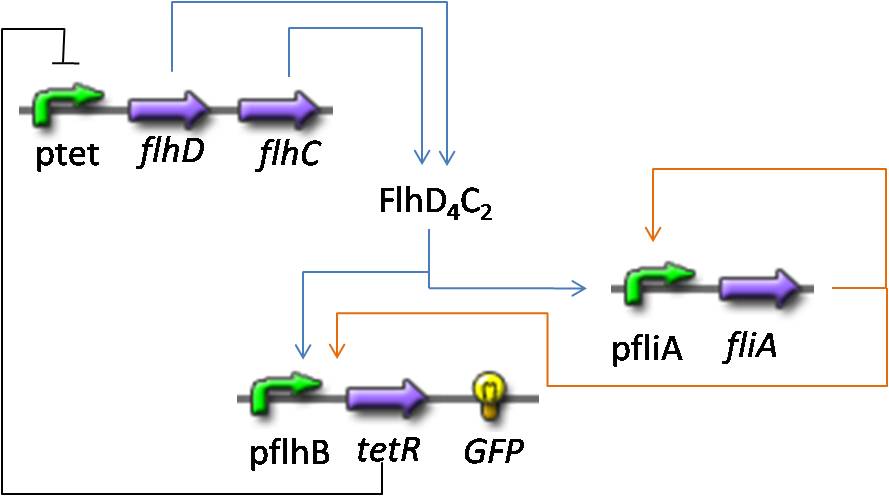
Simulations and Mathematical analysis
OscillationsShort System
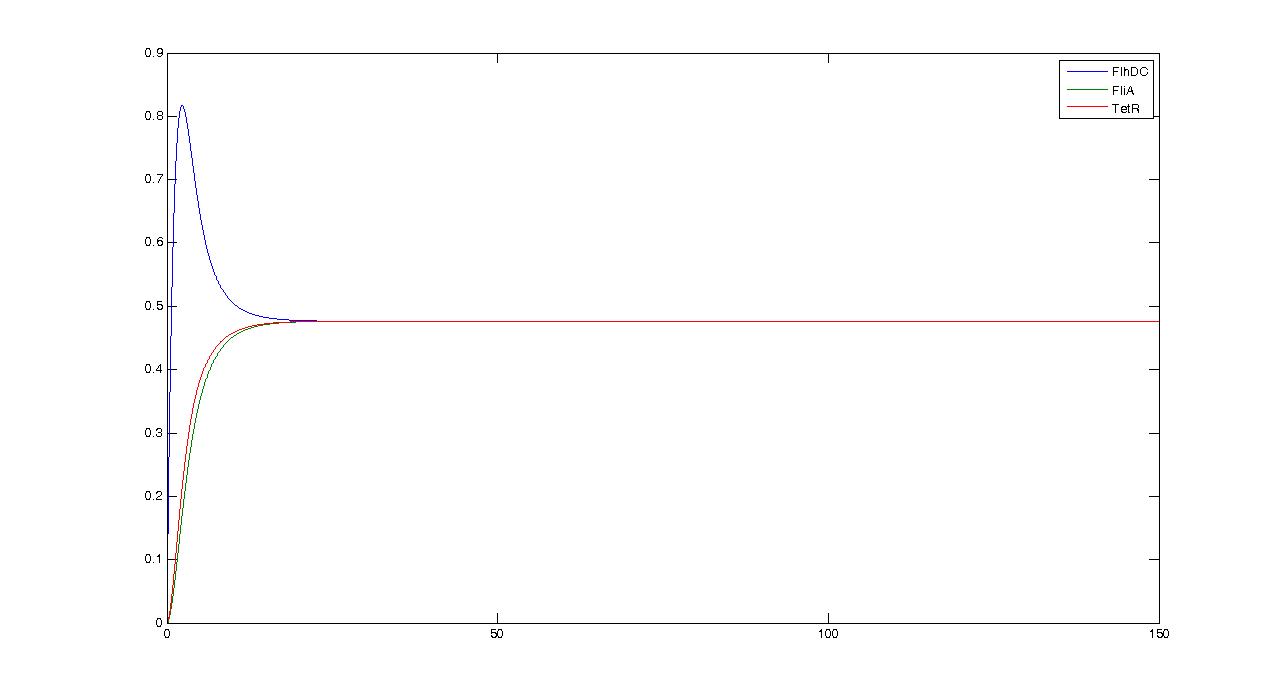
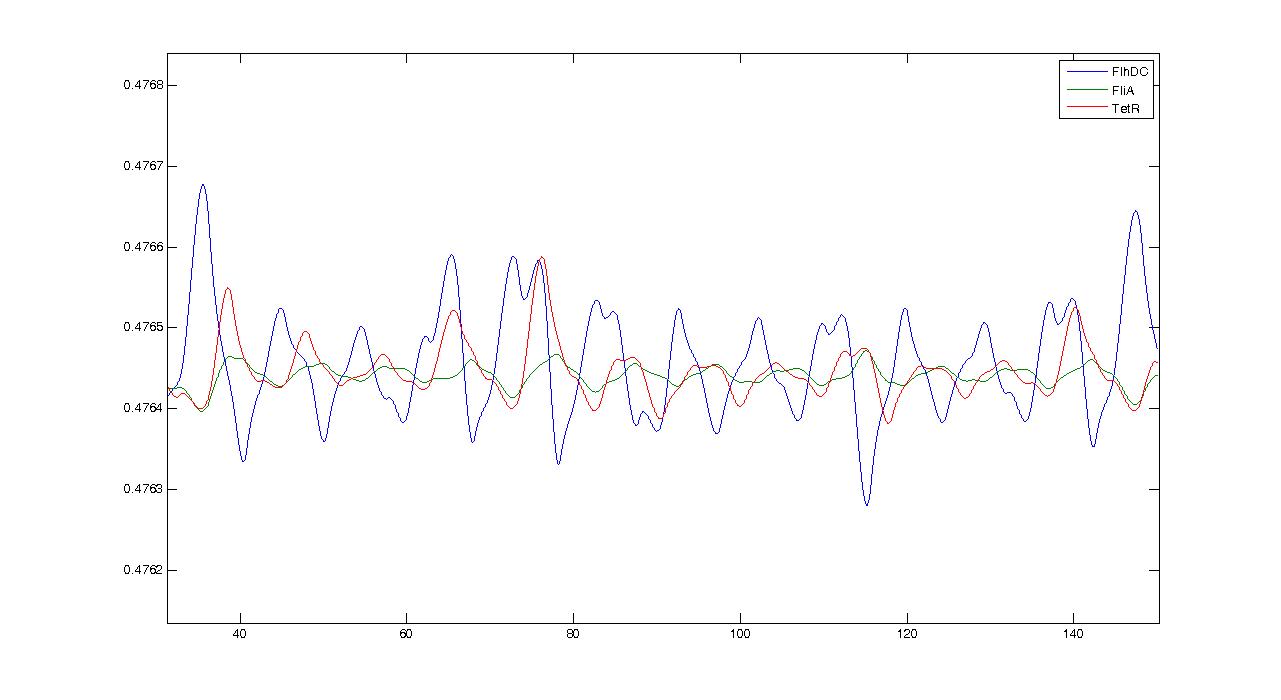
Observations---> petites oscillations + vérifier par le calcul ---> trop grande réactivité de flhDC
Understanding the dynamics
Then, we evaluate the jacobian matrix, so as to put the system under its linearized form: which gives : Then, we want to find the eigenvalues of the jacobian matrix, because they make us understand the behavior of the system. For example (since it is the case for our system), let us assume that we gave one real eigenvalue, and two imaginary ones. expliqeur lexp de matrix puis donner le charpolu puis donner la période Using these elements to improve the system and give directions to the wet-labEntire System//biocham ici//+ comparaison avec le modele hillistique FIFO
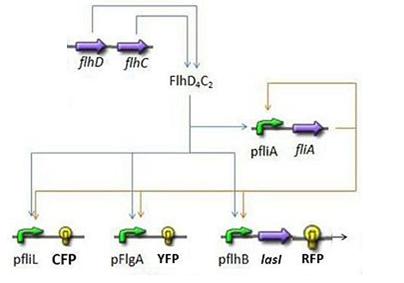
Here is the system we implementated using Matlab (see the corresponding codes) and the corresponding equations (for more detailed information see our establishment of the model). where CFP, YFP, and RFP will be denoted below as respectively Z1,Z2 and Z3.
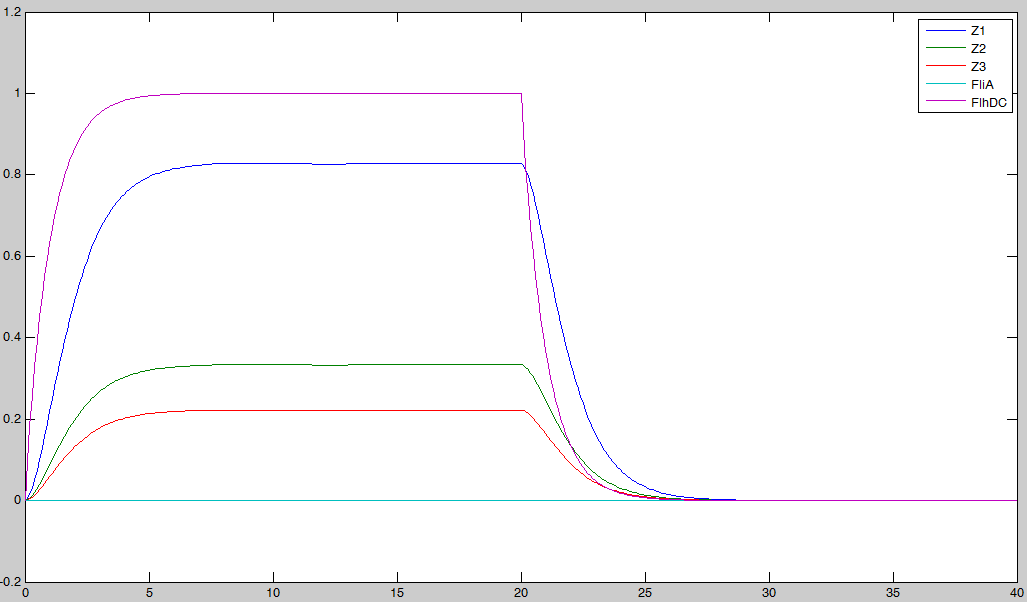
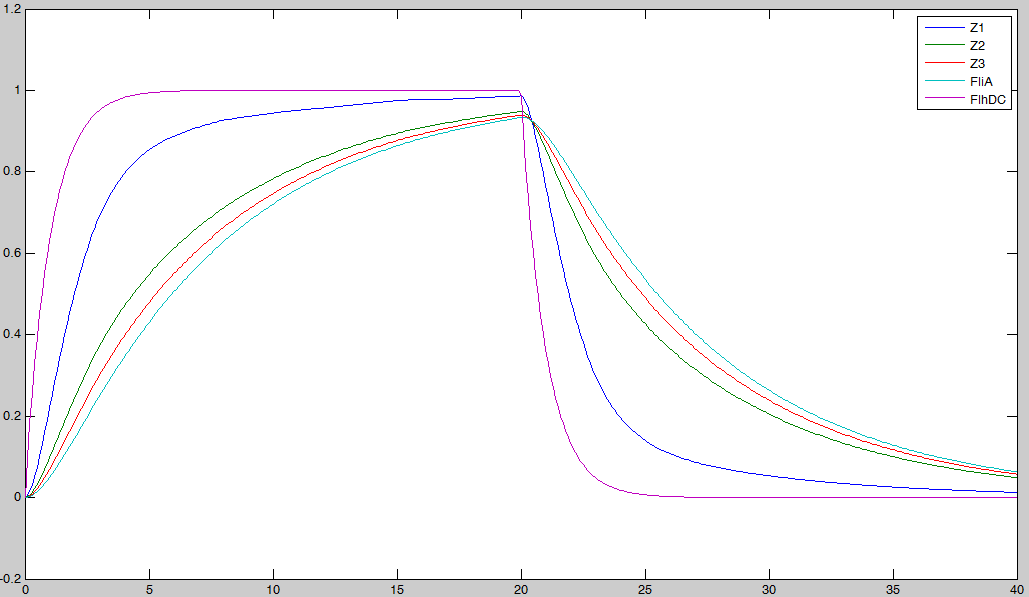
In fact we assumed that this behavior for FlhDC was acceptable regarding its estimated behavior in the whole system.
We may see that there is a LIFO behavior rather than the FIFO we expect...
SynchronizationMathematical AnalysisSimulations and verification of the hypothesis |
|||||||||||||||||||
 "
"