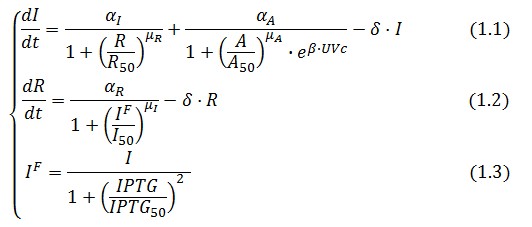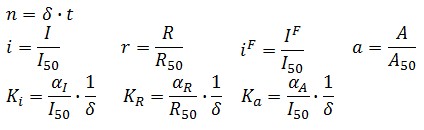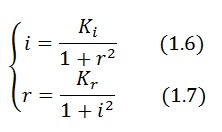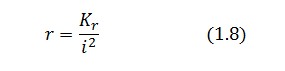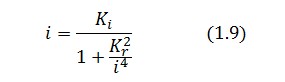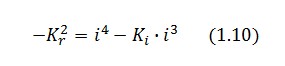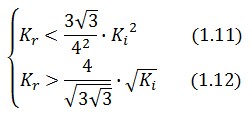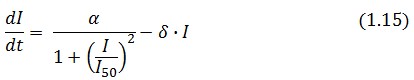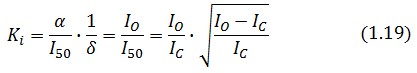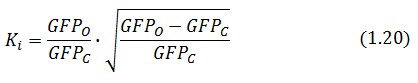Team:Bologna/Modeling
From 2008.igem.org
(→The genetic Flip-Flop) |
(→The genetic Flip-Flop) |
||
| (273 intermediate revisions not shown) | |||
| Line 1: | Line 1: | ||
<html> | <html> | ||
<style type="text/css"> | <style type="text/css"> | ||
| - | + | ||
body {background-color:#000000} | body {background-color:#000000} | ||
strong {color: #c09a6d;} | strong {color: #c09a6d;} | ||
| Line 11: | Line 11: | ||
[[Image:Logo1a.gif|220px]][[Image:Testata_dx.jpg|745px]] | [[Image:Logo1a.gif|220px]][[Image:Testata_dx.jpg|745px]] | ||
!align="center"|[[Team:Bologna|HOME]] | !align="center"|[[Team:Bologna|HOME]] | ||
| + | !align="center"|[[Team:Bologna/Project|PROJECT]] | ||
!align="center"|[[Team:Bologna/Team|TEAM]] | !align="center"|[[Team:Bologna/Team|TEAM]] | ||
| - | !align="center"|[[Team:Bologna/ | + | !align="center"|[[Team:Bologna/Software|SOFTWARE]] |
!align="center"|[[Team:Bologna/Modeling|MODELING]] | !align="center"|[[Team:Bologna/Modeling|MODELING]] | ||
| - | !align="center"|[[Team:Bologna/ | + | !align="center"|[[Team:Bologna/Wetlab|WET LAB]] |
| - | !align="center"|[[Team:Bologna/ | + | !align="center"|[[Team:Bologna/Notebook|LAB-BOOK]] |
!align="center"|[[Team:Bologna/Parts|SUBMITTED PARTS]] | !align="center"|[[Team:Bologna/Parts|SUBMITTED PARTS]] | ||
!align="center"|[[Team:Bologna/Biosafety|BIOSAFETY AND PROTOCOLS]] | !align="center"|[[Team:Bologna/Biosafety|BIOSAFETY AND PROTOCOLS]] | ||
| - | |||
|} | |} | ||
| + | |||
<br> | <br> | ||
| - | + | <div style="text-align:justify"> | |
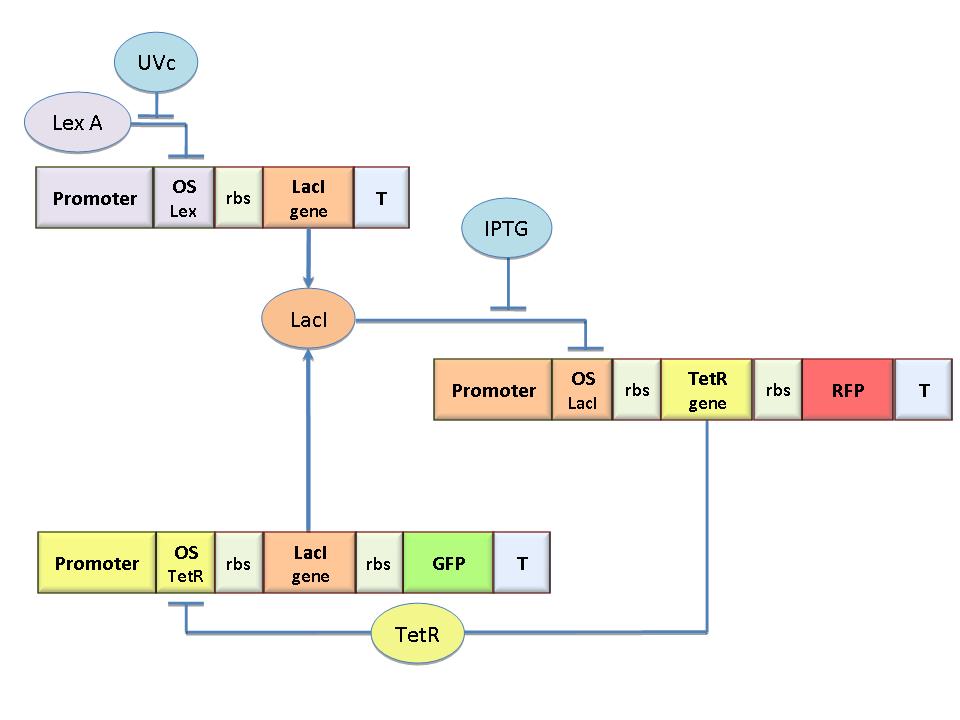
= Model-based analysis of the genetic Flip-Flop = | = Model-based analysis of the genetic Flip-Flop = | ||
| - | |||
== The genetic Flip-Flop == | == The genetic Flip-Flop == | ||
| - | <br> | + | [[Image:Circuito2.jpg|300px|thumb|right|Figure 1. Scheme of the genetic Flip-Flop]] |
| + | <div style="text-align:justify"> | ||
| + | The molecular circuit in Figure 1 can switch between two different stable states (LacI-ON and TetR-ON), driven by two external stimuli (UVc and IPTG). LacI-ON represents the stable state in which LacI gene is active and LacI protein represses the TetR gene expression, with a positive feedback. Therefore, the LacI-ON state coincides with the TetR-OFF condition. On the contrary, the TetR-ON represents the state with the TetR gene active and the LacI gene silenced (LacI-OFF). Owing to the coexistence of two stable states (bistability), this circuit is capable of serving as a binary memory [Collins et al. 2000]. We denominated it a Flip-Flop since it works as a [[Team:Bologna/Modeling#SR_Latch|SR Latch]]: LacI state is the [[Image:q.jpg]] output and TetR state is the [[Image:qneg.jpg]] output. Uvc is the set signal and IPTG is the reset signal. Indeed, IPTG stimulation inhibits LacI repressor, thus can cause the transition from the LacI-ON state to the TetR-ON. UVc radiation, inactivating LexA repressor through the [[Team:Bologna/Modeling#UV_Radiation:_SOS_system|SOS response]] [Friedberg et al. 1995] can cause the opposite transition from LacI-ON to TetR-ON.<br> | ||
| + | The core elements of the genetic program are two mutually regulated promoters. The promoter transcriptional strength and the repressor binding affinity to the promoter determinate such relevant circuit properties as the bistability and the response to inputs. To quote the promoters in terms of strength and sensitivity to repressor we resorted to the following model-based analysis and [[Team:Bologna/Modeling#Numerical_simulations|numerical simulations]]. | ||
| - | |||
| - | |||
| - | |||
| + | [https://2008.igem.org/Team:Bologna/Modeling ''Up''] | ||
| - | + | == Mathematical Model == | |
| - | + | ||
| - | |||
| - | < | + | '''<font size="3">Model equations</font>''' |
| - | |||
<br> | <br> | ||
The Flip-Flop circuit in Figure 1 can be modeled by the following equations: | The Flip-Flop circuit in Figure 1 can be modeled by the following equations: | ||
| + | |||
| + | <br> | ||
| + | |||
[[Image:Equazioni.jpg|center]] | [[Image:Equazioni.jpg|center]] | ||
| + | |||
<br> | <br> | ||
| + | |||
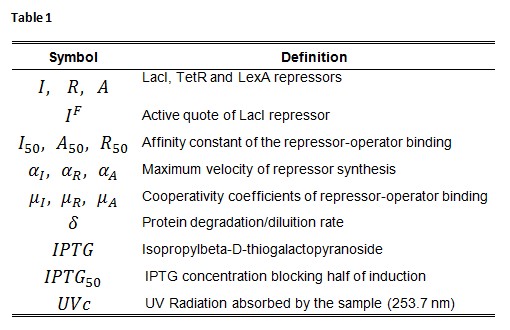
Symbol definition is listed in Table 1. | Symbol definition is listed in Table 1. | ||
| + | |||
| + | <br> | ||
[[Image:Tabella simboli.jpg|center]] | [[Image:Tabella simboli.jpg|center]] | ||
| + | |||
| + | <br> | ||
| + | |||
| + | A common motif in repressor proteins is the presence of a dimeric nucleotide-binding site with dimeric structure. In accordance to this general structure the cooperativity coefficients ([[Image:mu.jpg]]) were assumed equal to 2. The maximum velocity of repressor synthesis ([[Image:alfa.jpg]]) accounts for the strength of the unregulated promoter and RBS. The value of the affinity constant for the binding of repressor to the promoter strictly depends on the sequence of operator site (OS block). | ||
| + | |||
<br> | <br> | ||
| - | |||
| - | = | + | '''<font size="3">Adimensional equations</font>''' |
<br> | <br> | ||
| Line 62: | Line 71: | ||
Where: | Where: | ||
| - | + | ||
<br> | <br> | ||
| + | |||
| + | [[Image:accozz.jpg|center]] | ||
| + | |||
| + | |||
[https://2008.igem.org/Team:Bologna/Modeling ''Up''] | [https://2008.igem.org/Team:Bologna/Modeling ''Up''] | ||
| - | |||
== Equibrium conditions == | == Equibrium conditions == | ||
| - | |||
In the absence of stimuli, the adimensional concentrations of LacI ([[Image:i.jpg]]) and TetR ([[Image:r.jpg]]) at equilibrium are related by the equations: | In the absence of stimuli, the adimensional concentrations of LacI ([[Image:i.jpg]]) and TetR ([[Image:r.jpg]]) at equilibrium are related by the equations: | ||
| Line 75: | Line 86: | ||
<br> | <br> | ||
To obtain these relations the UVc-dependent term in equation (1.4) was ignored ([[Image:appr.jpg]] ). This is justified by the high binding constant of LexA for its operator, and the consequent negligible contribution to the LacI synthesis. | To obtain these relations the UVc-dependent term in equation (1.4) was ignored ([[Image:appr.jpg]] ). This is justified by the high binding constant of LexA for its operator, and the consequent negligible contribution to the LacI synthesis. | ||
| - | Equations (1.6) and (1.7) can have one or three solutions that represent the equilibrium conditions of the circuit. The solutions, i.e. the equilibrium conditions, can be graphically identified as the intersections between [[Image:r.jpg]] and [[Image:i.jpg]] nullclines (see Figure 2). The case of multiple equilibrium conditions (bistability case) is shown in Figure 2 panel b | + | Equations (1.6) and (1.7) can have one or three solutions that represent the equilibrium conditions of the circuit. The solutions, i.e. the equilibrium conditions, can be graphically identified as the intersections between [[Image:r.jpg]] and [[Image:i.jpg]] nullclines (see Figure 2). The case of multiple equilibrium conditions (bistability case) is shown in Figure 2 panel b. TetR-ON and LacI-ON are stable equilibria separated by the unstable one (saddle point). Due to the bistability the circuit can operate as a binary memory. |
| - | The existence of a bistability condition depends on the value of [[Image:kr.jpg]] and [[Image:ki.jpg]] parameters. If [[Image:kr.jpg]] decrease (see Figure 2 | + | The existence of a bistability condition depends on the value of [[Image:kr.jpg]] and [[Image:ki.jpg]] parameters. If [[Image:kr.jpg]] decrease (see Figure 2 panel a) a saddle-node bifurcation can occur, TetR-ON equilibrium vanishes and remain only the stable equilibrium LacI-ON. The contrary occurs when [[Image:ki.jpg]] is decreased (Figure 2 panel c). Thus bistability is guaranteed only for a limited range of [[Image:ki.jpg]] and [[Image:kr.jpg]] values. |
| - | |||
<br> | <br> | ||
| + | |||
| + | [[Image:equicondition.jpg|900px|center|thumbnail|Figure 2. Equilibrium conditions]] | ||
| + | |||
| + | |||
| + | [https://2008.igem.org/Team:Bologna/Modeling ''Up''] | ||
== Bifurcation analysis == | == Bifurcation analysis == | ||
| Line 99: | Line 114: | ||
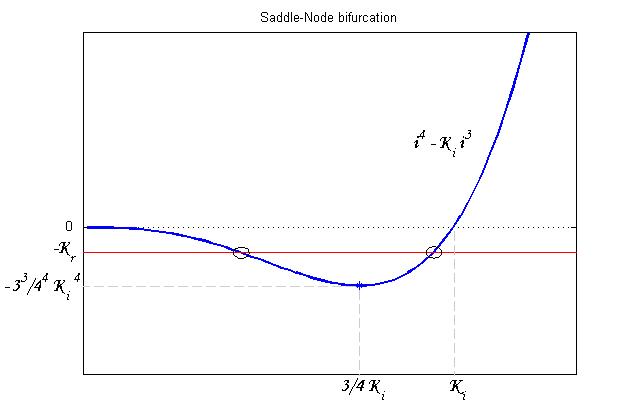
To be real the solutions of equation (1.10) it is necessary that [[Image:krdis.jpg]] (see Figure 3). Under this condition the existence of the LacI-ON state is assured. When [[Image:kreq.jpg]] the system undergoes a saddle-node bifurcation (LacI-ON and saddle point go in collision) and the two equilibrium points vanish. | To be real the solutions of equation (1.10) it is necessary that [[Image:krdis.jpg]] (see Figure 3). Under this condition the existence of the LacI-ON state is assured. When [[Image:kreq.jpg]] the system undergoes a saddle-node bifurcation (LacI-ON and saddle point go in collision) and the two equilibrium points vanish. | ||
<br> | <br> | ||
| - | [[Image: | + | [[Image:SaddleNodebifurcation1.jpg|thumbnail|center|500 px|Figure 3. Saddle-Node bifurcation]] |
<br> | <br> | ||
An analogous result can be obtained for the existence of the TetR-ON state. Thus, a sufficient condition for bistability is: | An analogous result can be obtained for the existence of the TetR-ON state. Thus, a sufficient condition for bistability is: | ||
| + | |||
| + | <br> | ||
[[Image:Equa1_11_12.jpg|center]] | [[Image:Equa1_11_12.jpg|center]] | ||
| + | |||
<br> | <br> | ||
| + | |||
Figure 4 shows the log-log plot of (1.11) and (1.12) | Figure 4 shows the log-log plot of (1.11) and (1.12) | ||
| + | |||
<br> | <br> | ||
| - | [[Image: | + | |
| + | [[Image:Rangeofbistability2.jpg|500 px|center|thumbnail|Figure 4. Range of bistability for the genetic Flip-Flop]] | ||
<br> | <br> | ||
| + | |||
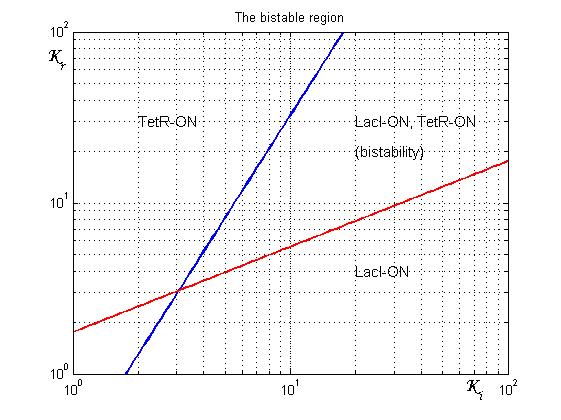
| + | As shown in Figure 4, the coexistence of two stable equilibria (LacI-ON and TerR-ON) is guaranteed for [[image:ki.jpg]]and [[image:kr.jpg]]greater than 3 in a large range of values (bistability range). Imposing a value for [[image:ki.jpg]] greater than 3 it is possible to establish a range for [[image:kr.jpg]] to have a bistable behaviour. More the ([[image:ki.jpg]],[[image:kr.jpg]]) point is near the bifurcation lines more the transition from bistability to monostability is probably. To have a good robustness we fixed [[image:ki.jpg]] and [[image:kr.jpg]] equal to 10. For this value the circuit is sufficently distant from the bifurcation lines to avoid random memory switching but it is possible to set (or to reset) the memory with proper stimulation. | ||
| + | |||
| + | |||
[https://2008.igem.org/Team:Bologna/Modeling ''Up''] | [https://2008.igem.org/Team:Bologna/Modeling ''Up''] | ||
| - | == Procedure for | + | == Procedure for Ki-index identification == |
<br> | <br> | ||
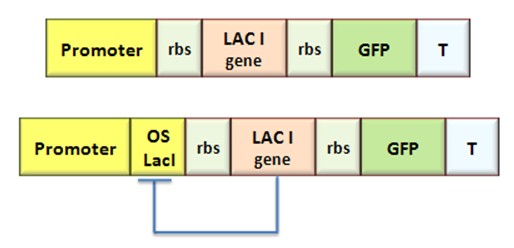
| - | The procedure will be described for LacI, analogous procedure can be applied to the TetR case. The value of [[Image:ki.jpg]] -index can be identified comparing the experimental responses of the open loop and closed loop circuits: | + | The procedure will be described for LacI, analogous procedure can be applied to the TetR case. The value of [[Image:ki.jpg]]-index can be identified comparing the experimental responses of the open loop and closed loop circuits: |
| - | + | ||
| - | + | ||
| - | + | ||
<br> | <br> | ||
| + | {| align="center" | ||
| + | | | ||
| + | <br><br> | ||
| + | * Open loop circuit | ||
| + | <br><br><br> | ||
| + | * Closed loop circuit | ||
| + | <br><br><br><br><br><br><br> | ||
| + | |[[Image:Molecularcircuitini.jpg|thumbnail|500px|Figure 5. Molecular circuits for the Ki-index experimental determination|right]] | ||
| + | |} | ||
| + | |||
| + | |||
| + | |||
The LacI concentration in the open loop circuit is given by: | The LacI concentration in the open loop circuit is given by: | ||
<br> | <br> | ||
| - | [[Image:Equa1_13.jpg]] | + | [[Image:Equa1_13.jpg|center]] |
<br> | <br> | ||
| - | |||
Thus the equilibrium condition is: | Thus the equilibrium condition is: | ||
<br> | <br> | ||
| - | [[Image:Equa1_14.jpg]] | + | [[Image:Equa1_14.jpg|center]] |
<br> | <br> | ||
The time derivative of LacI concentration in the close loop circuit follows: | The time derivative of LacI concentration in the close loop circuit follows: | ||
<br> | <br> | ||
| - | [[Image:Equa1_15.jpg]] | + | [[Image:Equa1_15.jpg|center]] |
<br> | <br> | ||
Which gives the equilibrium condition: | Which gives the equilibrium condition: | ||
<br> | <br> | ||
| - | [[Image:Equa1_16.jpg]] | + | [[Image:Equa1_16.jpg|center]] |
<br> | <br> | ||
That can be rewritten | That can be rewritten | ||
<br> | <br> | ||
| - | [[Image:Equa1_17.jpg]] | + | [[Image:Equa1_17.jpg|center]] |
<br> | <br> | ||
| - | The affinity | + | The affinity constant can consequently be derived from this expression |
<br> | <br> | ||
| - | [[Image:Equa1_18.jpg]] | + | [[Image:Equa1_18.jpg|center]] |
<br> | <br> | ||
Inserting the (1.14) and (1.18) in the [[Image:ki.jpg]]-index definition one obtain: | Inserting the (1.14) and (1.18) in the [[Image:ki.jpg]]-index definition one obtain: | ||
<br> | <br> | ||
| - | [[Image:Equa1_19b.jpg]] | + | [[Image:Equa1_19b.jpg|center]] |
<br> | <br> | ||
We assume that GFP is proportion to [[Image:imai.jpg]], then | We assume that GFP is proportion to [[Image:imai.jpg]], then | ||
<br> | <br> | ||
| - | [[Image:Equa1_20.jpg]] | + | [[Image:Equa1_20.jpg|center]] |
<br> | <br> | ||
We introduce the ratio [[Image:h.jpg]] between the fluorescence in open loop and in closed loop: | We introduce the ratio [[Image:h.jpg]] between the fluorescence in open loop and in closed loop: | ||
<br> | <br> | ||
| - | [[Image:Equa1_21.jpg]] | + | [[Image:Equa1_21.jpg|center]] |
<br> | <br> | ||
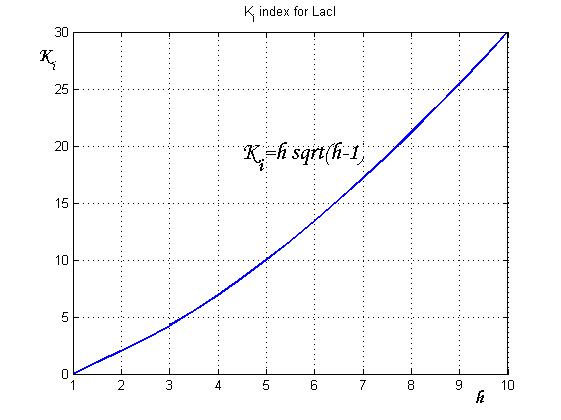
After measuring the ratio [[Image:h.jpg]] it is possible to calculate [[Image:ki.jpg]] by the curve in Figure 6 and then it is possible to establish by Figure 4 the [[Image:kr.jpg]] range that guarantees bistability. In the presence of an experimentally characterized library of regulated promoter, the procedure can be adopted to design genetic Flip-Flop with desired behaviors.<br> | After measuring the ratio [[Image:h.jpg]] it is possible to calculate [[Image:ki.jpg]] by the curve in Figure 6 and then it is possible to establish by Figure 4 the [[Image:kr.jpg]] range that guarantees bistability. In the presence of an experimentally characterized library of regulated promoter, the procedure can be adopted to design genetic Flip-Flop with desired behaviors.<br> | ||
| - | [[Image: | + | [[Image:indexforlaci1.jpg|center|thumbnail|500 px|Figure 6. Ki-index for LacI]] |
| - | == Numerical | + | |
| - | [[Image: | + | [https://2008.igem.org/Team:Bologna/Modeling ''Up''] |
| - | [[Image: | + | |
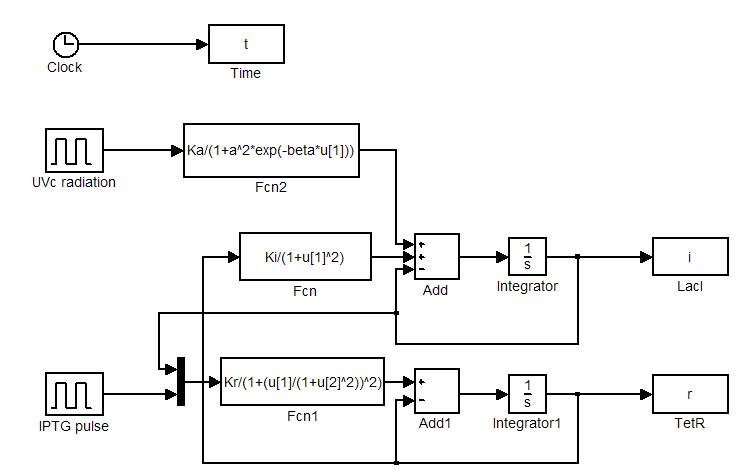
| + | == Numerical simulations== | ||
| + | |||
| + | Model equations (1.4) and (1.5) have been used to simulate: i) the sensitivity of the circuit to initial state and ii) the response to [[Image:iptgn.jpg]] and [[Team:Bologna/Wetlab#UV_Induction|UVc stimulations]]. Numerical simulations were performed in Simulink (MathWorks). Simulator scheme is shown in Figure 7. To ensure circuit bistability parameters [[Image:ki.jpg]] and [[Image:kr.jpg]] were both fixed to 10. | ||
| + | |||
| + | <br> | ||
| + | |||
| + | [[Image:blocchi1.jpg|center|500 px|thumbnail|Figure 7. Simulink simulator scheme]] | ||
| + | |||
| + | <br> | ||
| + | |||
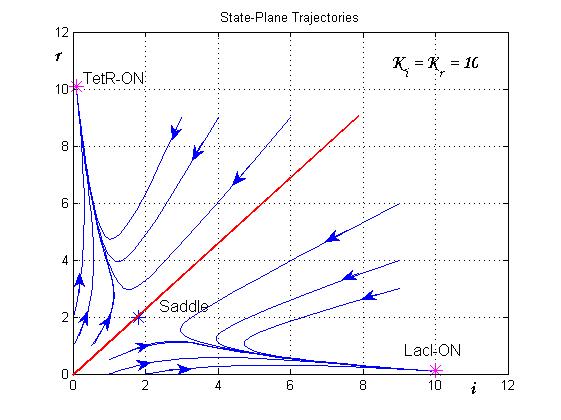
| + | The trajectories in the plane of the states (see Figure 8) clearly show the separatrix line (red line) and two attraction basins (one for the LacI-ON and the other for TetR-ON equilibrium). Depending on the initial state the memory can reach one of two stable equilibria (blu curve). The memory switches from a stable equilibrium to the other one when an external perturbation move the state over the separatrix entering it in the other attraction basin. | ||
| + | |||
| + | <br> | ||
| + | |||
| + | [[Image:sim2.jpg|center|500 px|thumbnail|Figure 8. State-Plane Trajectories]] | ||
| + | |||
| + | <br> | ||
| + | |||
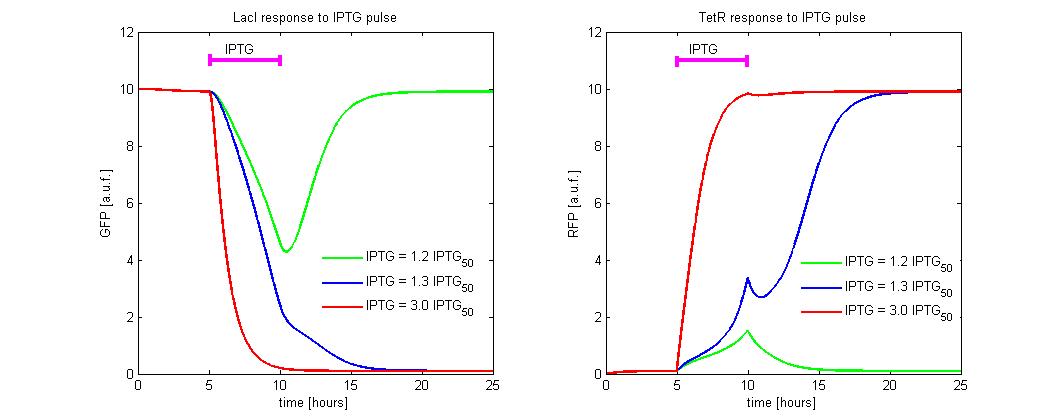
| + | To simulate the [[Image:iptgn.jpg]] reset, we fixed the initial state to the LacI-ON ([[Image:i.jpg]] = 10 and [[Image:r.jpg]] = 0.2) and we simulate the application of different levels of [[Image:iptgn.jpg]]. In the simulations we referred the [[Image:iptgn.jpg]] to the [[Image:iptg50.jpg]] concentration. An induction of maximum 5 hours was considered (see Figure 9). Until [[Image:iptgn.jpg]] level is lower than 1.2 times the [[Image:iptg50.jpg]], the memory does not reset to TetR-ON and when the induction finish, the state returns in about 5 hours to LacI-ON. To observe the memory switching is necessary to overcome the separatrix. This occurs for [[Image:iptgn.jpg]] > 1.2 times [[Image:iptg50.jpg]]. With a minimal [[Image:iptgn.jpg]] dose the switching is very slow (about 5 hour). To accelerate the transition it is sufficient to expose the circuit for 1 hour to [[Image:iptgn.jpg]] = 3 times [[Image:iptg50.jpg]]. | ||
| + | |||
| + | <br> | ||
| + | |||
| + | [[Image:iptg4.jpg|center|500 px|thumbnail|Figure 9. Circuit response to IPTG pulse]] | ||
| + | |||
| + | <br> | ||
| + | |||
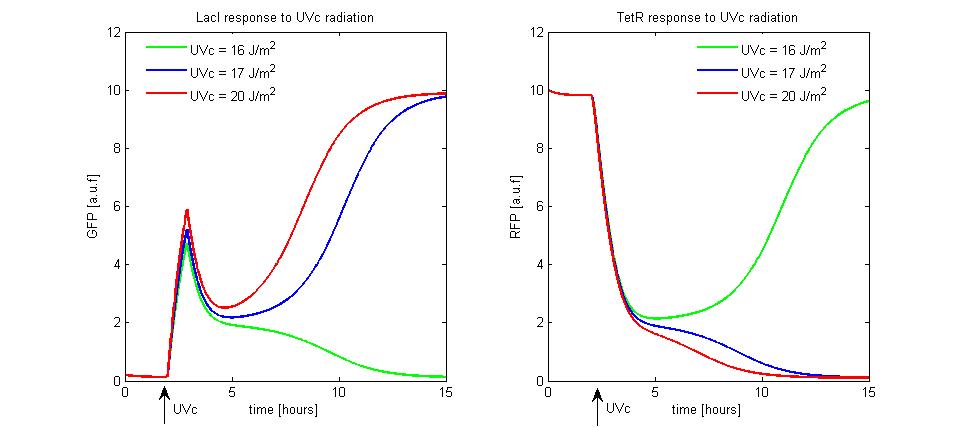
| + | To simulate the UVc set to LacI-ON of the memory, we assumed the TetR-ON as initial condition ([[Image:i.jpg]] = 0.2 and [[Image:r.jpg]] = 10), [[Image:ka.jpg]] parameter was fixed equal to 10, the rate [[Image:aa50.jpg]] was equal to 30 and [[Image:1beta.jpg]] was equal to 2. We supposed to radiate the memory for few minutes with different UVc energies. The cell radiation starts the SOS response that we simple modeled as a temporary RecA-mediated inhibition of LexA repressor. The memory set to LacI-ON does not take place until the UVc energy is lower than a threshold of 16 [[Image:udm.jpg]] (see Figure 10). When the UVc exceeds this threshold, the memory switches from TetR-ON to LacI-ON. | ||
| + | |||
| + | <br> | ||
| + | |||
| + | [[Image:UVc1.jpg|center|500 px|thumbnail|Figure 10. Circuit response to UVc radiation]] | ||
| + | |||
| + | |||
| + | [https://2008.igem.org/Team:Bologna/Modeling ''Up''] | ||
| + | |||
| + | = SR Latch = | ||
| + | |||
| + | In digital circuits, a Flip-Flop is a term referring to an electronic circuit (a bistable multivibrator) that has two stable states and thereby is capable of serving as one bit of memory. Today, the term Flip-Flop has come to mostly denote non-transparent (clocked or edge-triggered) devices, while the simpler transparent ones are often referred to as '''latches'''; however, as this distinction is quite new, the two words are sometimes used interchangeably. | ||
| + | |||
| + | A Flip-Flop is usually controlled by one or two control signals and/or a gate or clock signal. The output often includes the complement as well as the normal output. As Flip-Flops are implemented electronically, they require power and ground connections. | ||
| + | |||
| + | Flip-Flops can be either simple (transparent) or clocked. Simple Flip-Flops can be built around a pair of cross-coupled inverting elements: vacuum tubes, bipolar transistors, field effect transistors, inverters, and inverting logic gates have all been used in practical circuits — perhaps augmented by some gating mechanism (an enable/disable input). The more advanced clocked (or non-transparent) devices are specially designed for synchronous (time-discrete) systems; such devices therefore ignores its inputs except at the transition of a dedicated clock signal (known as clocking, pulsing, or strobing). This causes the Flip-Flop to either change or retain its output signal based upon the values of the input signals at the transition. Some Flip-Flops change output on the rising edge of the clock, others on the falling edge. | ||
| + | |||
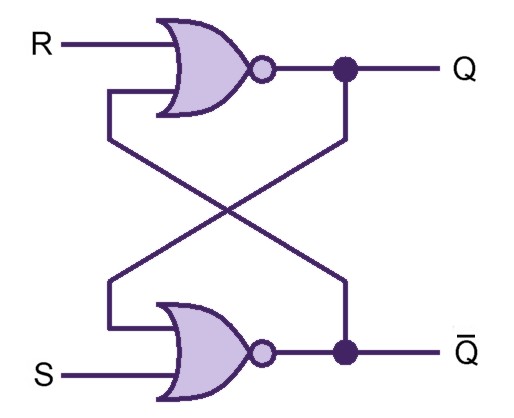
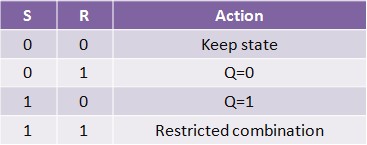
| + | Our project simulates a SR Latch (Figure 11), the most fundamental latch, where S and R stand for set and reset. It can be constructed from a pair of cross-coupled NOR logic gates. The stored bit is present on the output marked Q (or the complement <span style="text-decoration:overline">Q</span>). | ||
| + | |||
| + | |||
| + | [[Image:latchSR.jpg|thumb|350px|Figure 11. SR latch|center]] | ||
| + | |||
| + | |||
| + | Normally, in storage mode, the S and R inputs are both low, and feedback maintains the Q and <span style="text-decoration:overline">Q</span> outputs in a constant state. If S (Set) is pulsed high while R is held low, then the Q output is forced high, and stays high when S returns low; similarly, if R (Reset) is pulsed high while S is held low, then the Q output is forced low, and stays low when R returns low (Figure 12). | ||
| + | |||
| + | |||
| + | [[Image:tablatchSR.jpg|thumb|300px|Figure 12. SR latch truth table|center]] | ||
| + | |||
| + | |||
| + | The R = S = 1 combination is called a restricted combination because, as both NOR gates then output zeros, it breaks the logical equation Q = not <span style="text-decoration:overline">Q</span>. The combination is also inappropriate in circuits where both inputs may go low simultaneously (i.e. a transition from restricted to keep). The output would lock at either 1 or 0 depending on the propagation time relations between the gates (a race condition). In certain implementations, it could also lead to longer ringings (damped oscillations) before the output settles, and thereby result in undetermined values (errors) in high-frequency digital circuits. This condition is therefore sometimes avoided. | ||
| + | |||
| + | |||
| + | [https://2008.igem.org/Team:Bologna/Modeling ''Up''] | ||
| + | |||
| + | =UV Radiation: SOS system = | ||
| + | |||
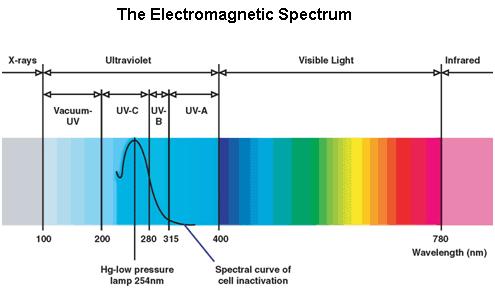
| + | Ultraviolet is that part of electromagnetic radiation bounded by the lower wavelength extreme of the visible spectrum and the upper end of the X-ray radiation band. The spectral range of ultraviolet radiation is, by definition, between 100 and 400 nm and is invisible to human eyes. The UV spectrum is subdivided into three bands: UV-A (long-wave) from 315 to 400 nm, UV-B (medium-wave) from 280 to 315 nm, UV-C (short-wave) from 100 to 280 nm. A strong germicidal effect is provided by the radiation in the short-wave UV-C band. | ||
| + | <br> | ||
| + | [[Image:spettro.jpg|center]] | ||
| + | <br> | ||
| + | [[Image:fosfoliasi.jpg|350px|thumbnail|Figure 13. After dimerization of two adjacent thymines blue light gives energy to photolyase to repair the damage |right]] | ||
| + | The maximum UV germicidal effect coincides with the peak absorbance of DNA (near 260nm) due to the dimerization of two adjacent thymines. | ||
| + | E.Coli cells have a system that recovery DNA damage when it occurs. The best studied transcriptional response to DNA damage is the SOS response [Friedberg et al 1995, Walker et al. 1996]. | ||
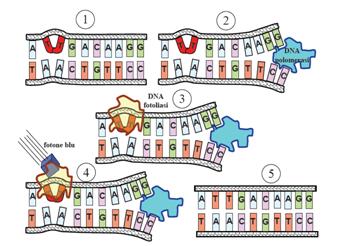
| + | This systems can be divided into two class: the SOS Photoreactivation repair and the SOS respond triggered by RecA protein. The first uses the photolyase, a poorly expressed enzyme(encoded by genes phrA and phrB) which binds the pyrimidine dimers and uses the blue light to split them apart as showed in Figure 13. | ||
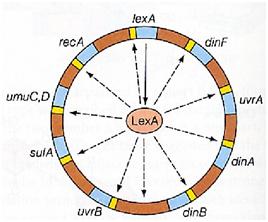
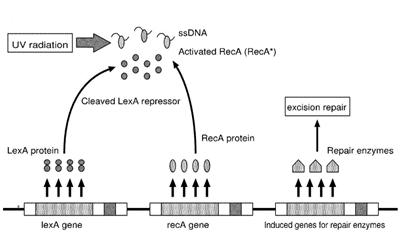
| + | Otherwise single stranded DNA produced by several DNA-damaging agents can be bound by RecA protein, resulting in conversion of this protein to its activated form. The RecA repair system doesn’t need light and Lexa protein controls the expression of 43 genes [Courcelle et al. (2001)] that cooperate together to repair the extensive genetic damage (Figure 14). RecA and LexA proteins play an important rule for the regulatory of SOS Recombination System. A LexA binding site is present in all the SOS promoters genes' and it works as a repressor of SOS system. In presence of DNA damage (DNA Single Strains) RecA becomes active and interacts with LexA protein, the repressor of the SOS genes [Wagner et al., 1999] . This interaction triggers the autocatalytic cleavage of LexA and consequent destruction of its ability to function as a repressor, which results in the derepression of SOS genes [Mustard and Little 2000; Fernandez De Henestrosa et al. 2000]. When the damage is repaired, DNA single strains are not present in the cell and the RecA protein no longer promotes the auto-cleavage of the LexA which is restored to its initial repression level (Figure 15).<br><br> | ||
| + | {| align="center" | ||
| + | |[[Image:lexa.jpg|thumbnail|350 px|Figure 14. SOS System controlled by LexA ]] | ||
| + | |width=70| | ||
| + | |[[Image:soslexa.jpg|thumbnail|350 px|Figure 15. Genes repressed by LexA]] | ||
| + | |||
| + | |} | ||
| + | |||
| + | |||
| + | [https://2008.igem.org/Team:Bologna/Modeling ''Up''] | ||
= Bibliography = | = Bibliography = | ||
| + | |||
| + | *Mads Kaern, William J.Blake, and J.J.Collins. The Engineering of Gene Regulatory Networks, Annu.Rev.Biomed.Eng.2003 5:179-206. | ||
| + | *Timothy S.Gardner, Charles R.Cantor & James J.Collins. Construction of a genetic toggle switch in Escherichia coli, Nature Vol.403 339-342. | ||
| + | *Nitzan Rosenfeld, Jonathan W.Young, Uri Alon, Peter S.Swain, Michael B.Elowitz. Gene Regulation at the Single-Cell Level. Science Vol 307 1962-1965. | ||
| + | *Sergej V.Aksenov. Dynamics of the inducing signal for the SOS regulatory system in Escherichia coli after ultraviolet irradiation. Mathematical Bioscienses 157 (1999) 269-286. | ||
| + | *Sandeep Krishna, Sergei Maslov, Kim Sneppen. UV-induced mutagenesis in Escherichia coli SOS response: A quantitative model. PLoS Comput Biol 3(3): e41. doi:10.1371/journal.pcbi.0030041. | ||
| + | *S.V.Aksenov et al. Mathematical model of SOS response regulation of an excision repair deficient mutant of Escherichia coli after ultraviolet light irradiation. J.theor.Biol (1997)186, 251-260. | ||
| + | *M.Sassanfar, J.W.Roberts. Nature of the SOS inducing signal in Escherichia coli: the involvement of DNA replication. J.Molec.Biol. 212 (1990) 79. | ||
| + | *R.Brent and M.Ptashne. Mechanism of action of the lexA gene production. Prot.Nat.Acad.Sci.USA Vol.78, No 7, 4204-4208, 1981. | ||
| + | *Friedberg, E.C., Walker, G.C., and Siede, W. DNA repair and mutagenesis. ASM Press, Washington, D.C. 1995. | ||
| + | *Walker, G.C. The SOS Response of Escherichia coli. In Escherichia coli and salmonella: Cellular and molecular biology (ed. F.C. Neidhardt, R. Curtiss III, J.L. Ingraham, E.C.C. Lin, K.B. Low, B. Magasanik, W.S. Reznikoff, M. Riley, M. Schaechter and H.E. Umbarger), pp. 1400-1416. ASM Press, Washington, D.C. 1996 | ||
| + | *Courcelle, J., A. Khodursky, B. Peter, P. O. Brown and P. C. Hanawalt, 2001 Comparative gene expression profiles following UV exposure in wild-type and SOS-deficient Escherichia coli. Genetics 158: 41–64. | ||
| + | *J. Wagner, P. Gruz, S.-R. Kim, M. Yamada, K. Matsui, R.P.P. Fuchs and T. Nohmi, The dinB gene encodes a novel Escherichia coli DNA polymerase (DNA pol IV) involved in mutagenesis. Mol. Cell 4 (1999), pp. 281–286. | ||
| + | *Mustard, J. A., Little, J. W. (2000). Analysis of Escherichia coli RecA Interactions with LexA, lambda CI, and UmuD by Site-Directed Mutagenesis of recA. J. Bacteriol. 182: 1659-1670. | ||
| + | *Fernandez De Henestrosa, A. R., Ogi, T., Aoyagi, S., Chafin, D., Hayes, J. J., Ohmori, H. & Woodgate, R. (2000). Identification of additional genes belonging to the LexA regulon in Escherichia coli. Mol Microbiol 35, 1560–1572. | ||
[https://2008.igem.org/Team:Bologna/Modeling ''Up''] | [https://2008.igem.org/Team:Bologna/Modeling ''Up''] | ||
Latest revision as of 03:29, 30 October 2008
| HOME | PROJECT | TEAM | SOFTWARE | MODELING | WET LAB | LAB-BOOK | SUBMITTED PARTS | BIOSAFETY AND PROTOCOLS |
|---|
Contents |
Model-based analysis of the genetic Flip-Flop
The genetic Flip-Flop
The molecular circuit in Figure 1 can switch between two different stable states (LacI-ON and TetR-ON), driven by two external stimuli (UVc and IPTG). LacI-ON represents the stable state in which LacI gene is active and LacI protein represses the TetR gene expression, with a positive feedback. Therefore, the LacI-ON state coincides with the TetR-OFF condition. On the contrary, the TetR-ON represents the state with the TetR gene active and the LacI gene silenced (LacI-OFF). Owing to the coexistence of two stable states (bistability), this circuit is capable of serving as a binary memory [Collins et al. 2000]. We denominated it a Flip-Flop since it works as a SR Latch: LacI state is the ![]() output and TetR state is the
output and TetR state is the ![]() output. Uvc is the set signal and IPTG is the reset signal. Indeed, IPTG stimulation inhibits LacI repressor, thus can cause the transition from the LacI-ON state to the TetR-ON. UVc radiation, inactivating LexA repressor through the SOS response [Friedberg et al. 1995] can cause the opposite transition from LacI-ON to TetR-ON.
output. Uvc is the set signal and IPTG is the reset signal. Indeed, IPTG stimulation inhibits LacI repressor, thus can cause the transition from the LacI-ON state to the TetR-ON. UVc radiation, inactivating LexA repressor through the SOS response [Friedberg et al. 1995] can cause the opposite transition from LacI-ON to TetR-ON.
The core elements of the genetic program are two mutually regulated promoters. The promoter transcriptional strength and the repressor binding affinity to the promoter determinate such relevant circuit properties as the bistability and the response to inputs. To quote the promoters in terms of strength and sensitivity to repressor we resorted to the following model-based analysis and numerical simulations.
Mathematical Model
Model equations
The Flip-Flop circuit in Figure 1 can be modeled by the following equations:
Symbol definition is listed in Table 1.
A common motif in repressor proteins is the presence of a dimeric nucleotide-binding site with dimeric structure. In accordance to this general structure the cooperativity coefficients (![]() ) were assumed equal to 2. The maximum velocity of repressor synthesis (
) were assumed equal to 2. The maximum velocity of repressor synthesis (![]() ) accounts for the strength of the unregulated promoter and RBS. The value of the affinity constant for the binding of repressor to the promoter strictly depends on the sequence of operator site (OS block).
) accounts for the strength of the unregulated promoter and RBS. The value of the affinity constant for the binding of repressor to the promoter strictly depends on the sequence of operator site (OS block).
Adimensional equations
The equations (1.1) and (1.2) can be written dimensionless:
Where:
Equibrium conditions
In the absence of stimuli, the adimensional concentrations of LacI (![]() ) and TetR (
) and TetR (![]() ) at equilibrium are related by the equations:
) at equilibrium are related by the equations:
To obtain these relations the UVc-dependent term in equation (1.4) was ignored (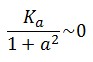 ). This is justified by the high binding constant of LexA for its operator, and the consequent negligible contribution to the LacI synthesis.
Equations (1.6) and (1.7) can have one or three solutions that represent the equilibrium conditions of the circuit. The solutions, i.e. the equilibrium conditions, can be graphically identified as the intersections between
). This is justified by the high binding constant of LexA for its operator, and the consequent negligible contribution to the LacI synthesis.
Equations (1.6) and (1.7) can have one or three solutions that represent the equilibrium conditions of the circuit. The solutions, i.e. the equilibrium conditions, can be graphically identified as the intersections between ![]() and
and ![]() nullclines (see Figure 2). The case of multiple equilibrium conditions (bistability case) is shown in Figure 2 panel b. TetR-ON and LacI-ON are stable equilibria separated by the unstable one (saddle point). Due to the bistability the circuit can operate as a binary memory.
The existence of a bistability condition depends on the value of
nullclines (see Figure 2). The case of multiple equilibrium conditions (bistability case) is shown in Figure 2 panel b. TetR-ON and LacI-ON are stable equilibria separated by the unstable one (saddle point). Due to the bistability the circuit can operate as a binary memory.
The existence of a bistability condition depends on the value of ![]() and
and ![]() parameters. If
parameters. If ![]() decrease (see Figure 2 panel a) a saddle-node bifurcation can occur, TetR-ON equilibrium vanishes and remain only the stable equilibrium LacI-ON. The contrary occurs when
decrease (see Figure 2 panel a) a saddle-node bifurcation can occur, TetR-ON equilibrium vanishes and remain only the stable equilibrium LacI-ON. The contrary occurs when ![]() is decreased (Figure 2 panel c). Thus bistability is guaranteed only for a limited range of
is decreased (Figure 2 panel c). Thus bistability is guaranteed only for a limited range of ![]() and
and ![]() values.
values.
Bifurcation analysis
Assuming that LacI-ON exists the corresponding equilibrium value of ![]() is higher than 1 (see Figure 2), then it can be assumed that
is higher than 1 (see Figure 2), then it can be assumed that ![]() and the equation (1.7) simplies to:
and the equation (1.7) simplies to:
Substituting this expression in equation (1.6) one obtain:
Then:
To be real the solutions of equation (1.10) it is necessary that 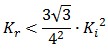 (see Figure 3). Under this condition the existence of the LacI-ON state is assured. When
(see Figure 3). Under this condition the existence of the LacI-ON state is assured. When ![]() the system undergoes a saddle-node bifurcation (LacI-ON and saddle point go in collision) and the two equilibrium points vanish.
the system undergoes a saddle-node bifurcation (LacI-ON and saddle point go in collision) and the two equilibrium points vanish.
An analogous result can be obtained for the existence of the TetR-ON state. Thus, a sufficient condition for bistability is:
Figure 4 shows the log-log plot of (1.11) and (1.12)
As shown in Figure 4, the coexistence of two stable equilibria (LacI-ON and TerR-ON) is guaranteed for ![]() and
and ![]() greater than 3 in a large range of values (bistability range). Imposing a value for
greater than 3 in a large range of values (bistability range). Imposing a value for ![]() greater than 3 it is possible to establish a range for
greater than 3 it is possible to establish a range for ![]() to have a bistable behaviour. More the (
to have a bistable behaviour. More the (![]() ,
,![]() ) point is near the bifurcation lines more the transition from bistability to monostability is probably. To have a good robustness we fixed
) point is near the bifurcation lines more the transition from bistability to monostability is probably. To have a good robustness we fixed ![]() and
and ![]() equal to 10. For this value the circuit is sufficently distant from the bifurcation lines to avoid random memory switching but it is possible to set (or to reset) the memory with proper stimulation.
equal to 10. For this value the circuit is sufficently distant from the bifurcation lines to avoid random memory switching but it is possible to set (or to reset) the memory with proper stimulation.
Procedure for Ki-index identification
The procedure will be described for LacI, analogous procedure can be applied to the TetR case. The value of ![]() -index can be identified comparing the experimental responses of the open loop and closed loop circuits:
-index can be identified comparing the experimental responses of the open loop and closed loop circuits:
|
|
The LacI concentration in the open loop circuit is given by:
Thus the equilibrium condition is:
The time derivative of LacI concentration in the close loop circuit follows:
Which gives the equilibrium condition:
That can be rewritten
The affinity constant can consequently be derived from this expression
Inserting the (1.14) and (1.18) in the ![]() -index definition one obtain:
-index definition one obtain:
We assume that GFP is proportion to ![]() , then
, then
We introduce the ratio ![]() between the fluorescence in open loop and in closed loop:
between the fluorescence in open loop and in closed loop:
After measuring the ratio ![]() it is possible to calculate
it is possible to calculate ![]() by the curve in Figure 6 and then it is possible to establish by Figure 4 the
by the curve in Figure 6 and then it is possible to establish by Figure 4 the ![]() range that guarantees bistability. In the presence of an experimentally characterized library of regulated promoter, the procedure can be adopted to design genetic Flip-Flop with desired behaviors.
range that guarantees bistability. In the presence of an experimentally characterized library of regulated promoter, the procedure can be adopted to design genetic Flip-Flop with desired behaviors.
Numerical simulations
Model equations (1.4) and (1.5) have been used to simulate: i) the sensitivity of the circuit to initial state and ii) the response to ![]() and UVc stimulations. Numerical simulations were performed in Simulink (MathWorks). Simulator scheme is shown in Figure 7. To ensure circuit bistability parameters
and UVc stimulations. Numerical simulations were performed in Simulink (MathWorks). Simulator scheme is shown in Figure 7. To ensure circuit bistability parameters ![]() and
and ![]() were both fixed to 10.
were both fixed to 10.
The trajectories in the plane of the states (see Figure 8) clearly show the separatrix line (red line) and two attraction basins (one for the LacI-ON and the other for TetR-ON equilibrium). Depending on the initial state the memory can reach one of two stable equilibria (blu curve). The memory switches from a stable equilibrium to the other one when an external perturbation move the state over the separatrix entering it in the other attraction basin.
To simulate the ![]() reset, we fixed the initial state to the LacI-ON (
reset, we fixed the initial state to the LacI-ON (![]() = 10 and
= 10 and ![]() = 0.2) and we simulate the application of different levels of
= 0.2) and we simulate the application of different levels of ![]() . In the simulations we referred the
. In the simulations we referred the ![]() to the
to the ![]() concentration. An induction of maximum 5 hours was considered (see Figure 9). Until
concentration. An induction of maximum 5 hours was considered (see Figure 9). Until ![]() level is lower than 1.2 times the
level is lower than 1.2 times the ![]() , the memory does not reset to TetR-ON and when the induction finish, the state returns in about 5 hours to LacI-ON. To observe the memory switching is necessary to overcome the separatrix. This occurs for
, the memory does not reset to TetR-ON and when the induction finish, the state returns in about 5 hours to LacI-ON. To observe the memory switching is necessary to overcome the separatrix. This occurs for ![]() > 1.2 times
> 1.2 times ![]() . With a minimal
. With a minimal ![]() dose the switching is very slow (about 5 hour). To accelerate the transition it is sufficient to expose the circuit for 1 hour to
dose the switching is very slow (about 5 hour). To accelerate the transition it is sufficient to expose the circuit for 1 hour to ![]() = 3 times
= 3 times ![]() .
.
To simulate the UVc set to LacI-ON of the memory, we assumed the TetR-ON as initial condition (![]() = 0.2 and
= 0.2 and ![]() = 10),
= 10), ![]() parameter was fixed equal to 10, the rate
parameter was fixed equal to 10, the rate ![]() was equal to 30 and
was equal to 30 and ![]() was equal to 2. We supposed to radiate the memory for few minutes with different UVc energies. The cell radiation starts the SOS response that we simple modeled as a temporary RecA-mediated inhibition of LexA repressor. The memory set to LacI-ON does not take place until the UVc energy is lower than a threshold of 16
was equal to 2. We supposed to radiate the memory for few minutes with different UVc energies. The cell radiation starts the SOS response that we simple modeled as a temporary RecA-mediated inhibition of LexA repressor. The memory set to LacI-ON does not take place until the UVc energy is lower than a threshold of 16 ![]() (see Figure 10). When the UVc exceeds this threshold, the memory switches from TetR-ON to LacI-ON.
(see Figure 10). When the UVc exceeds this threshold, the memory switches from TetR-ON to LacI-ON.
SR Latch
In digital circuits, a Flip-Flop is a term referring to an electronic circuit (a bistable multivibrator) that has two stable states and thereby is capable of serving as one bit of memory. Today, the term Flip-Flop has come to mostly denote non-transparent (clocked or edge-triggered) devices, while the simpler transparent ones are often referred to as latches; however, as this distinction is quite new, the two words are sometimes used interchangeably.
A Flip-Flop is usually controlled by one or two control signals and/or a gate or clock signal. The output often includes the complement as well as the normal output. As Flip-Flops are implemented electronically, they require power and ground connections.
Flip-Flops can be either simple (transparent) or clocked. Simple Flip-Flops can be built around a pair of cross-coupled inverting elements: vacuum tubes, bipolar transistors, field effect transistors, inverters, and inverting logic gates have all been used in practical circuits — perhaps augmented by some gating mechanism (an enable/disable input). The more advanced clocked (or non-transparent) devices are specially designed for synchronous (time-discrete) systems; such devices therefore ignores its inputs except at the transition of a dedicated clock signal (known as clocking, pulsing, or strobing). This causes the Flip-Flop to either change or retain its output signal based upon the values of the input signals at the transition. Some Flip-Flops change output on the rising edge of the clock, others on the falling edge.
Our project simulates a SR Latch (Figure 11), the most fundamental latch, where S and R stand for set and reset. It can be constructed from a pair of cross-coupled NOR logic gates. The stored bit is present on the output marked Q (or the complement Q).
Normally, in storage mode, the S and R inputs are both low, and feedback maintains the Q and Q outputs in a constant state. If S (Set) is pulsed high while R is held low, then the Q output is forced high, and stays high when S returns low; similarly, if R (Reset) is pulsed high while S is held low, then the Q output is forced low, and stays low when R returns low (Figure 12).
The R = S = 1 combination is called a restricted combination because, as both NOR gates then output zeros, it breaks the logical equation Q = not Q. The combination is also inappropriate in circuits where both inputs may go low simultaneously (i.e. a transition from restricted to keep). The output would lock at either 1 or 0 depending on the propagation time relations between the gates (a race condition). In certain implementations, it could also lead to longer ringings (damped oscillations) before the output settles, and thereby result in undetermined values (errors) in high-frequency digital circuits. This condition is therefore sometimes avoided.
UV Radiation: SOS system
Ultraviolet is that part of electromagnetic radiation bounded by the lower wavelength extreme of the visible spectrum and the upper end of the X-ray radiation band. The spectral range of ultraviolet radiation is, by definition, between 100 and 400 nm and is invisible to human eyes. The UV spectrum is subdivided into three bands: UV-A (long-wave) from 315 to 400 nm, UV-B (medium-wave) from 280 to 315 nm, UV-C (short-wave) from 100 to 280 nm. A strong germicidal effect is provided by the radiation in the short-wave UV-C band.
The maximum UV germicidal effect coincides with the peak absorbance of DNA (near 260nm) due to the dimerization of two adjacent thymines.
E.Coli cells have a system that recovery DNA damage when it occurs. The best studied transcriptional response to DNA damage is the SOS response [Friedberg et al 1995, Walker et al. 1996].
This systems can be divided into two class: the SOS Photoreactivation repair and the SOS respond triggered by RecA protein. The first uses the photolyase, a poorly expressed enzyme(encoded by genes phrA and phrB) which binds the pyrimidine dimers and uses the blue light to split them apart as showed in Figure 13.
Otherwise single stranded DNA produced by several DNA-damaging agents can be bound by RecA protein, resulting in conversion of this protein to its activated form. The RecA repair system doesn’t need light and Lexa protein controls the expression of 43 genes [Courcelle et al. (2001)] that cooperate together to repair the extensive genetic damage (Figure 14). RecA and LexA proteins play an important rule for the regulatory of SOS Recombination System. A LexA binding site is present in all the SOS promoters genes' and it works as a repressor of SOS system. In presence of DNA damage (DNA Single Strains) RecA becomes active and interacts with LexA protein, the repressor of the SOS genes [Wagner et al., 1999] . This interaction triggers the autocatalytic cleavage of LexA and consequent destruction of its ability to function as a repressor, which results in the derepression of SOS genes [Mustard and Little 2000; Fernandez De Henestrosa et al. 2000]. When the damage is repaired, DNA single strains are not present in the cell and the RecA protein no longer promotes the auto-cleavage of the LexA which is restored to its initial repression level (Figure 15).
Bibliography
- Mads Kaern, William J.Blake, and J.J.Collins. The Engineering of Gene Regulatory Networks, Annu.Rev.Biomed.Eng.2003 5:179-206.
- Timothy S.Gardner, Charles R.Cantor & James J.Collins. Construction of a genetic toggle switch in Escherichia coli, Nature Vol.403 339-342.
- Nitzan Rosenfeld, Jonathan W.Young, Uri Alon, Peter S.Swain, Michael B.Elowitz. Gene Regulation at the Single-Cell Level. Science Vol 307 1962-1965.
- Sergej V.Aksenov. Dynamics of the inducing signal for the SOS regulatory system in Escherichia coli after ultraviolet irradiation. Mathematical Bioscienses 157 (1999) 269-286.
- Sandeep Krishna, Sergei Maslov, Kim Sneppen. UV-induced mutagenesis in Escherichia coli SOS response: A quantitative model. PLoS Comput Biol 3(3): e41. doi:10.1371/journal.pcbi.0030041.
- S.V.Aksenov et al. Mathematical model of SOS response regulation of an excision repair deficient mutant of Escherichia coli after ultraviolet light irradiation. J.theor.Biol (1997)186, 251-260.
- M.Sassanfar, J.W.Roberts. Nature of the SOS inducing signal in Escherichia coli: the involvement of DNA replication. J.Molec.Biol. 212 (1990) 79.
- R.Brent and M.Ptashne. Mechanism of action of the lexA gene production. Prot.Nat.Acad.Sci.USA Vol.78, No 7, 4204-4208, 1981.
- Friedberg, E.C., Walker, G.C., and Siede, W. DNA repair and mutagenesis. ASM Press, Washington, D.C. 1995.
- Walker, G.C. The SOS Response of Escherichia coli. In Escherichia coli and salmonella: Cellular and molecular biology (ed. F.C. Neidhardt, R. Curtiss III, J.L. Ingraham, E.C.C. Lin, K.B. Low, B. Magasanik, W.S. Reznikoff, M. Riley, M. Schaechter and H.E. Umbarger), pp. 1400-1416. ASM Press, Washington, D.C. 1996
- Courcelle, J., A. Khodursky, B. Peter, P. O. Brown and P. C. Hanawalt, 2001 Comparative gene expression profiles following UV exposure in wild-type and SOS-deficient Escherichia coli. Genetics 158: 41–64.
- J. Wagner, P. Gruz, S.-R. Kim, M. Yamada, K. Matsui, R.P.P. Fuchs and T. Nohmi, The dinB gene encodes a novel Escherichia coli DNA polymerase (DNA pol IV) involved in mutagenesis. Mol. Cell 4 (1999), pp. 281–286.
- Mustard, J. A., Little, J. W. (2000). Analysis of Escherichia coli RecA Interactions with LexA, lambda CI, and UmuD by Site-Directed Mutagenesis of recA. J. Bacteriol. 182: 1659-1670.
- Fernandez De Henestrosa, A. R., Ogi, T., Aoyagi, S., Chafin, D., Hayes, J. J., Ohmori, H. & Woodgate, R. (2000). Identification of additional genes belonging to the LexA regulon in Escherichia coli. Mol Microbiol 35, 1560–1572.
 "
"