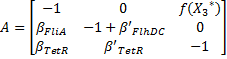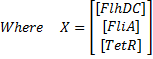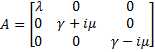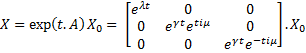Team:Paris/Modeling/BOB/Simulations page travail
From 2008.igem.org
(→Understanding the dynamics) |
(→Understanding the dynamics) |
||
| Line 83: | Line 83: | ||
[[Image:DE5.jpg|center]] | [[Image:DE5.jpg|center]] | ||
| - | + | The λ and γ coefficient make the convergence. In our case they are negative terms, which explains the fact that we have a quick convergence for the system. Ideally, it could be convenient to find which parameter influence this coefficient, so as to play with it and be able to propose a better control of the convergence. | |
| - | + | <br> | |
| + | The μ coefficient is responsible for the oscillations. In fact, in another base, with only real matrix, this would beget cosinuses and sinuses terms. Furthermore, it is strongly linked to the period of the oscillations. | ||
| + | <br> | ||
| + | We can hereby prove that the small oscillations observed before are not induced by a simulation artefact. With the parameters presented in the array before, we have evaluated the equilibrium values by solving | ||
| + | [[Image:Math0.jpg|center]] | ||
| + | We obtained three solutions : | ||
| + | <center> | ||
| + | -0.2382 - 0.6139i | ||
| + | -0.2382 + 0.6139i | ||
| + | 0.4764 | ||
| + | </center> | ||
| + | We are only interested in positive real solutions. We can note that 0.4764 corresponds well to the experimental equilibrium value. | ||
| + | Then we evaluated the eigenvalues for the jacobian : | ||
| + | <center> | ||
| + | -1.0159 + 0.5042i | ||
| + | -1.0159 - 0.5042i | ||
| + | -0.1111 | ||
| + | </center> | ||
=== Using these elements to improve the system and give directions to the wet-lab === | === Using these elements to improve the system and give directions to the wet-lab === | ||
Revision as of 10:10, 7 October 2008
|
(Under Construction : synchronisation and whole system)
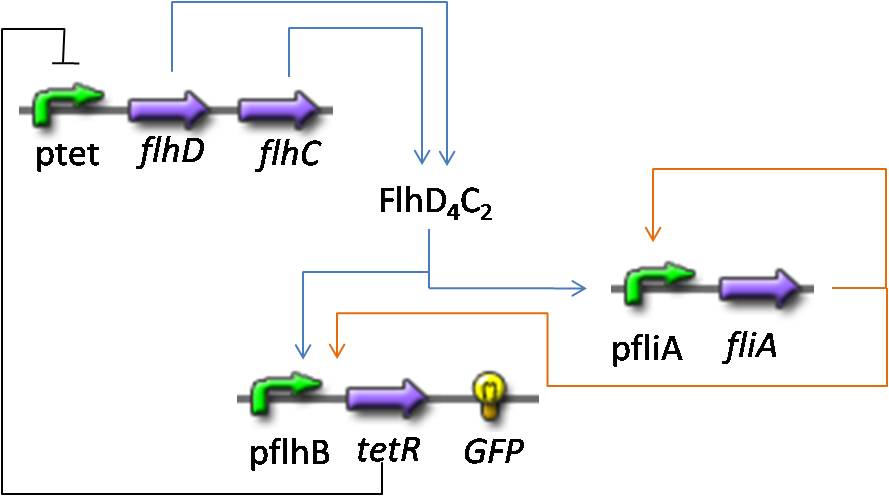
Simulations and Mathematical analysis
OscillationsShort System
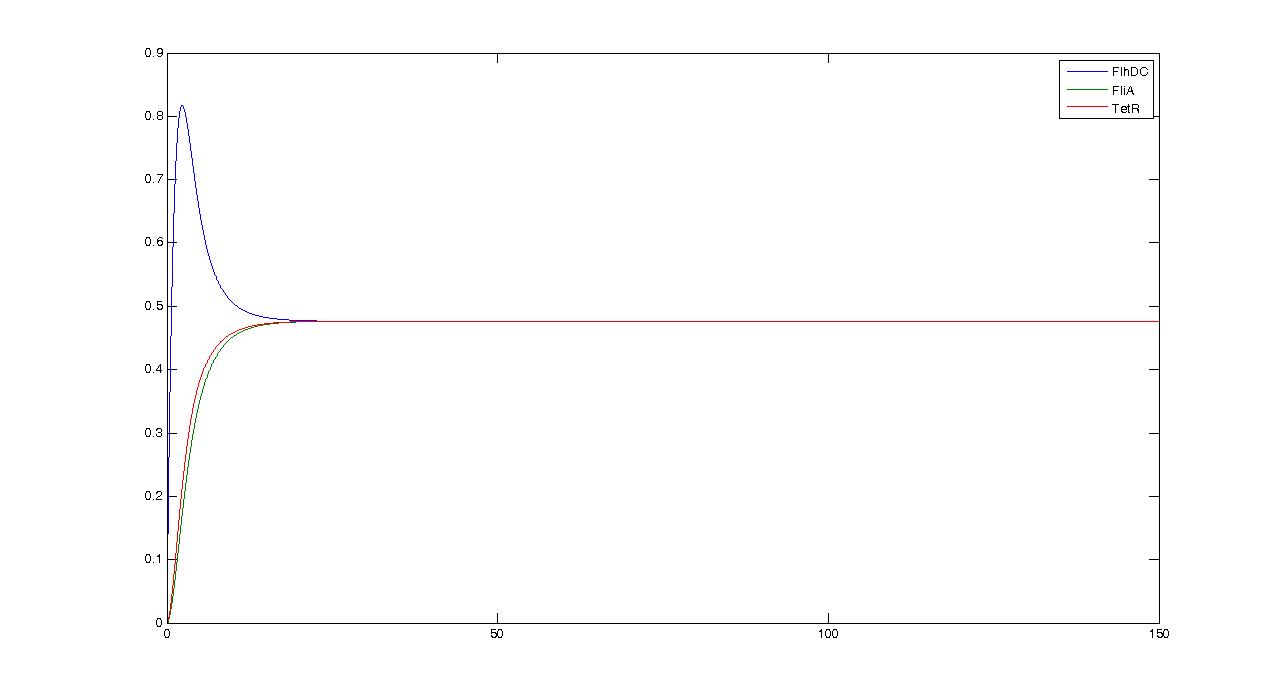
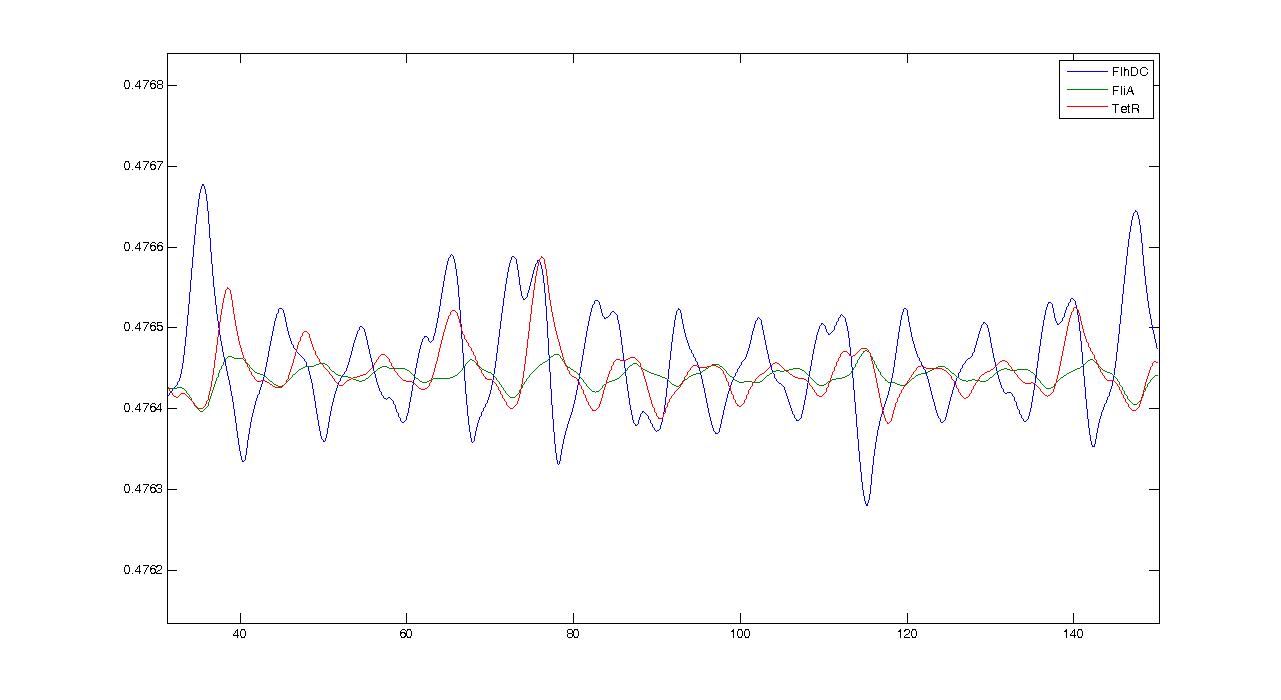
Observations---> petites oscillations + vérifier par le calcul ---> trop grande réactivité de flhDC
Understanding the dynamics
Then, we evaluate the jacobian matrix, so as to put the system under its linearized form:
which gives : Then, we want to find the eigenvalues of the jacobian matrix, because they make us understand the behavior of the system. Here is the theoretical explanation : The λ and γ coefficient make the convergence. In our case they are negative terms, which explains the fact that we have a quick convergence for the system. Ideally, it could be convenient to find which parameter influence this coefficient, so as to play with it and be able to propose a better control of the convergence.
We obtained three solutions : -0.2382 - 0.6139i -0.2382 + 0.6139i 0.4764 We are only interested in positive real solutions. We can note that 0.4764 corresponds well to the experimental equilibrium value. Then we evaluated the eigenvalues for the jacobian : -1.0159 + 0.5042i -1.0159 - 0.5042i -0.1111 Using these elements to improve the system and give directions to the wet-labdire qu'on peut tester les solutions pour obtenir une partie réelle aussi faible que possible, et qu'on peut jouer sur la période au moins dire que pb c'es que mm en dim3, ca devient cho de gérer,mm si c la dim minimale Entire System//biocham ici//+ comparaison avec le modele hillistique FIFO
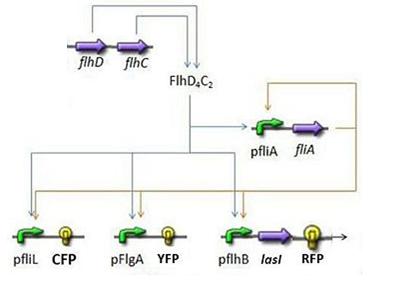
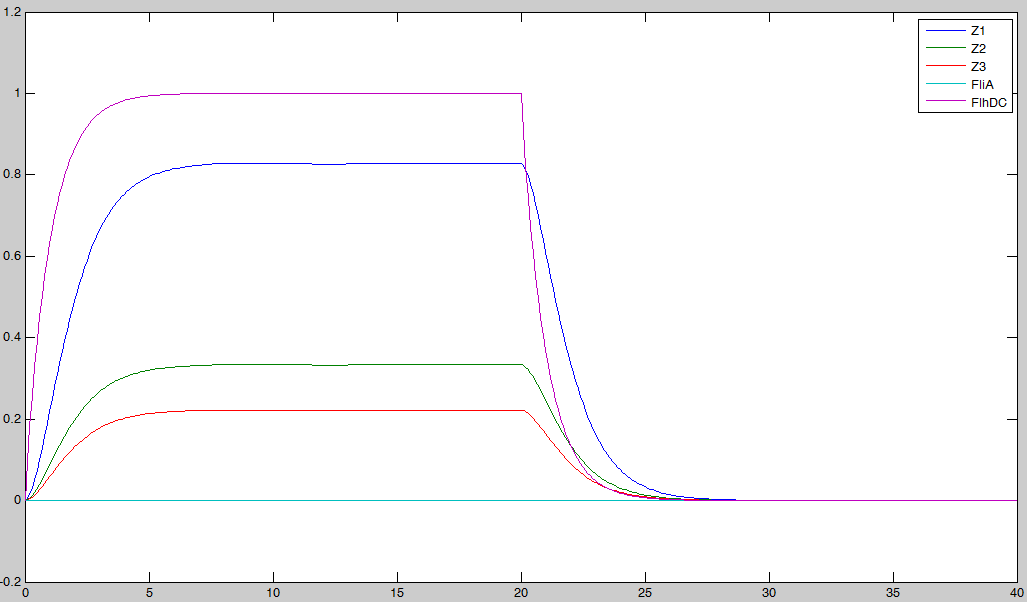
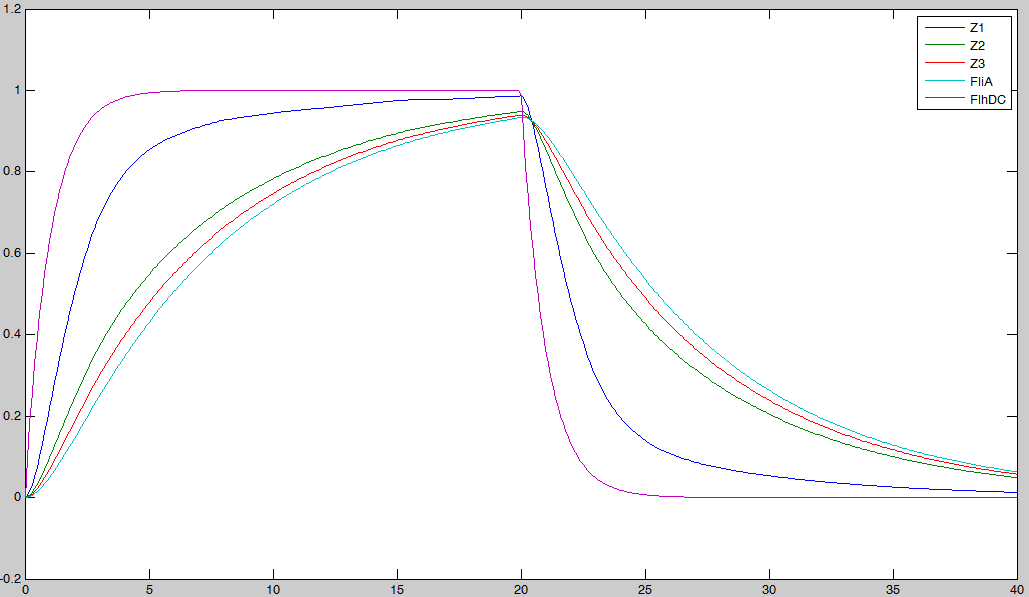
Here is the system we implementated using Matlab (see the corresponding codes) and the corresponding equations (for more detailed information see our establishment of the model). where CFP, YFP, and RFP will be denoted below as respectively Z1,Z2 and Z3.
In fact we assumed that this behavior for FlhDC was acceptable regarding its estimated behavior in the whole system.
We may see that there is a LIFO behavior rather than the FIFO we expect...
SynchronizationMathematical AnalysisSimulations and verification of the hypothesis |
|||||||||||||||||||
 "
"