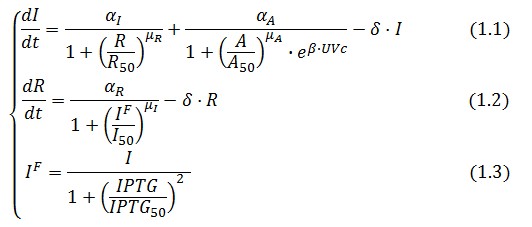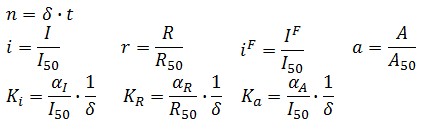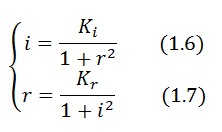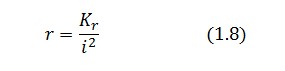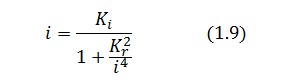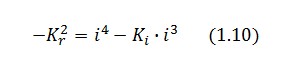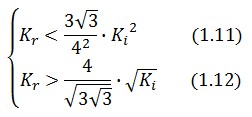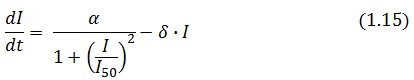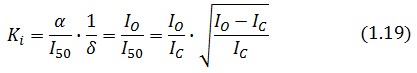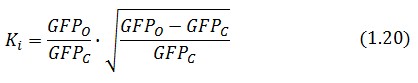Team:Bologna/Modeling
From 2008.igem.org
(→JK Flip-Flop) |
(→JK Flip-Flop) |
||
| Line 174: | Line 174: | ||
A flip-flop is usually controlled by one or two control signals and/or a gate or clock signal. The output often includes the complement as well as the normal output. As flip-flops are implemented electronically, they require power and ground connections. | A flip-flop is usually controlled by one or two control signals and/or a gate or clock signal. The output often includes the complement as well as the normal output. As flip-flops are implemented electronically, they require power and ground connections. | ||
| + | Flip-flops can be either simple (transparent) or clocked. Simple flip-flops can be built around a pair of cross-coupled inverting elements: vacuum tubes, bipolar transistors, field effect transistors, inverters, and inverting logic gates have all been used in practical circuits — perhaps augmented by some gating mechanism (an enable/disable input). The more advanced clocked (or non-transparent) devices are specially designed for synchronous (time-discrete) systems; such devices therefore ignores its inputs except at the transition of a dedicated clock signal (known as clocking, pulsing, or strobing). This causes the flip-flop to either change or retain its output signal based upon the values of the input signals at the transition. Some flip-flops change output on the rising edge of the clock, others on the falling edge. | ||
| + | |||
| + | Clocked flip-flops are typically implemented as master-slave devices[3] where two basic flip-flops (plus some additional logic) collaborate to make it insensitive to spikes and noise between the short clock transitions; they nevertheless also often include asynchronous clear or set inputs which may be used to change the current output independent of the clock. | ||
| + | |||
| + | Flip-flops can be further divided into types that have found common applicability in both asynchronous and clocked sequential systems: the SR ("set-reset"), D ("data" or "delay"[4]), T ("toggle"), and JK types are the common ones; all of which may be synthesized from (most) other types by a few logic gates. The behavior of a particular type can be described by what is termed the characteristic equation, which derives the "next" (i.e., after the next clock pulse) output, Qnext, in terms of the input signal(s) and/or the current output, Q. | ||
[https://2008.igem.org/Team:Bologna/Project ''Up''] | [https://2008.igem.org/Team:Bologna/Project ''Up''] | ||
Revision as of 09:14, 29 October 2008
| HOME | PROJECT | TEAM | SOFTWARE | MODELING | WET LAB | LAB-BOOK | SUBMITTED PARTS | BIOSAFETY AND PROTOCOLS |
|---|
Contents |
Model-based analysis of the genetic Flip-Flop
The genetic Flip-Flop
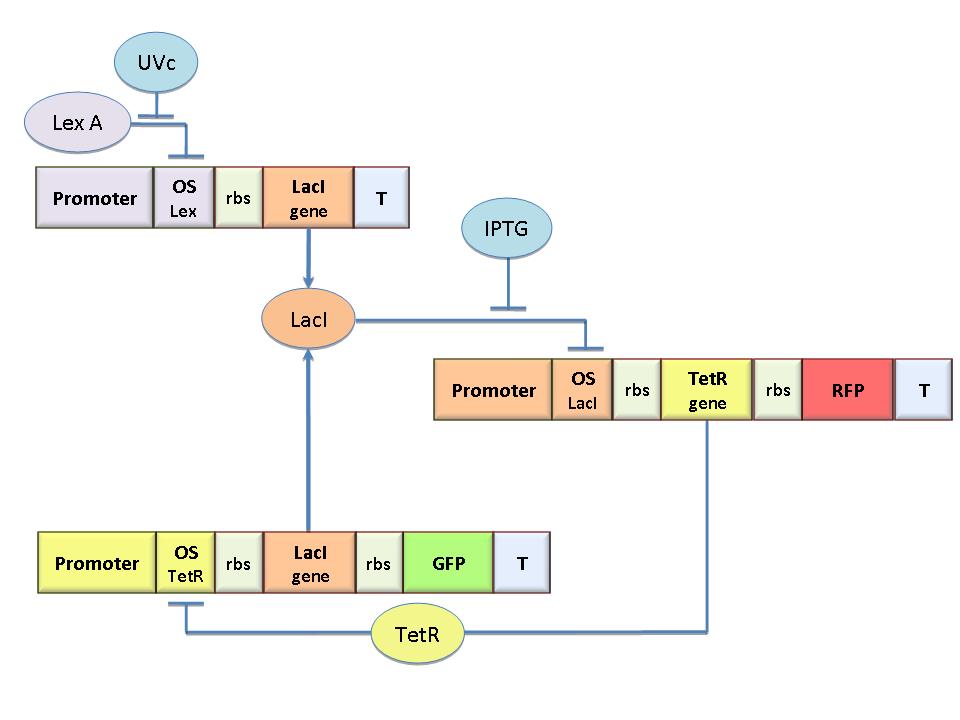
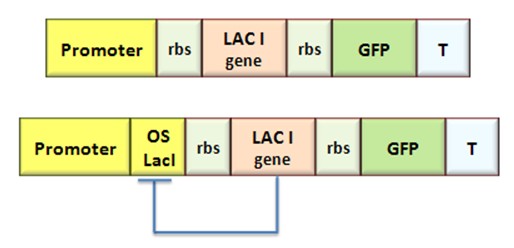
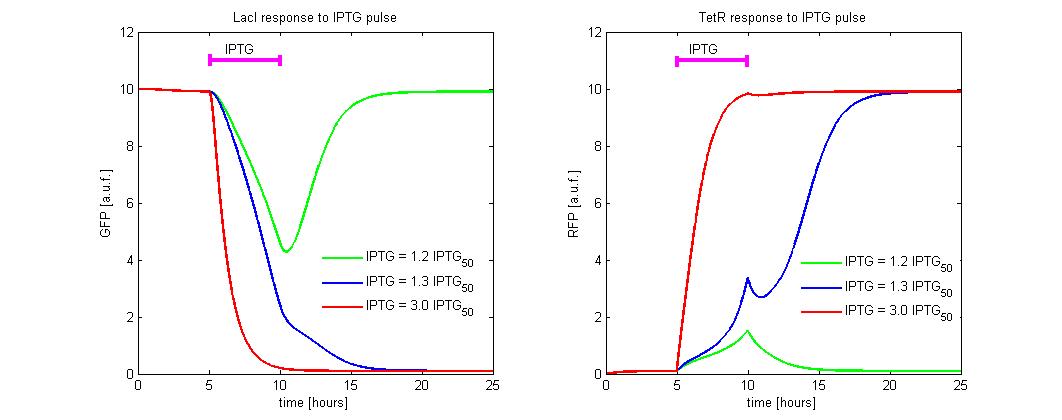
The molecular circuit in Figure 1 can switch between two different stable states (LacI-ON and TetR-ON), driven by two external stimuli (UVc and IPTG). LacI-ON represents the stable state where the LacI gene is active and LacI protein represses TetR gene expression, in a positive feedback. Therefore, the LacI-ON state coincides with the TetR-OFF condition. On the contrary, the TetR-ON represents the state with the TetR gene active and the LacI gene silenced (LacI-OFF). Owing to the coexistence of two stable states (bistability), this circuit is capable of serving as a binary of memory. We denominated it a Flip-Flop since it works as a SR Latch: LacI state is the ![]() output and TetR state is the
output and TetR state is the ![]() output. Uvc is the set signal and IPTG is the reset signal. Indeed, IPTG stimulation inhibits LacI repressor, thus can cause the transition from the LacI-ON state to the TetR-ON. UVc radiation, inactivating LexA repressor through the SOS response (Friedberg et al., 1995) can cause the opposite transition from LacI-ON to TetR-ON.
output. Uvc is the set signal and IPTG is the reset signal. Indeed, IPTG stimulation inhibits LacI repressor, thus can cause the transition from the LacI-ON state to the TetR-ON. UVc radiation, inactivating LexA repressor through the SOS response (Friedberg et al., 1995) can cause the opposite transition from LacI-ON to TetR-ON.
Mathematical Model
Model equations
The Flip-Flop circuit in Figure 1 can be modeled by the following equations:
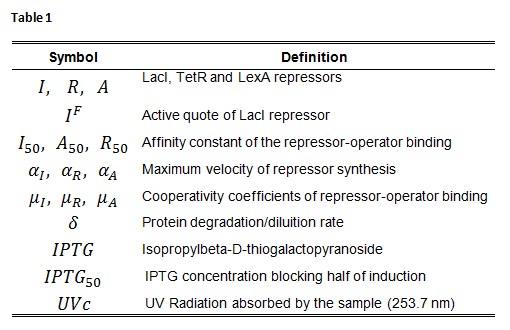
Symbol definition is listed in Table 1.
A common motif in repressor proteins is the presence of a dimeric nucleotide-binding site with dimeric structure. In accordance to this general structure the cooperativity coefficients ![]() were assumed equal to 2. The maximum velocity of repressor synthesis
were assumed equal to 2. The maximum velocity of repressor synthesis ![]() accounts for the strength of the unregulated promoter and RBS. The value of the affinity constant for the binding of repressor to the promoter strictly depends on the sequence of operator site (OS block).
accounts for the strength of the unregulated promoter and RBS. The value of the affinity constant for the binding of repressor to the promoter strictly depends on the sequence of operator site (OS block).
Adimensional equations
The equations (1.1) and (1.2) can be written dimensionless:
Where:
Equibrium conditions
In the absence of stimuli, the adimensional concentrations of LacI (![]() ) and TetR (
) and TetR (![]() ) at equilibrium are related by the equations:
) at equilibrium are related by the equations:
To obtain these relations the UVc-dependent term in equation (1.4) was ignored (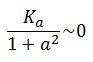 ). This is justified by the high binding constant of LexA for its operator, and the consequent negligible contribution to the LacI synthesis.
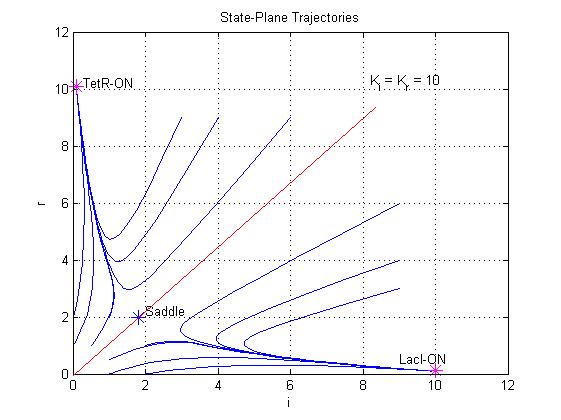
Equations (1.6) and (1.7) can have one or three solutions that represent the equilibrium conditions of the circuit. The solutions, i.e. the equilibrium conditions, can be graphically identified as the intersections between
). This is justified by the high binding constant of LexA for its operator, and the consequent negligible contribution to the LacI synthesis.
Equations (1.6) and (1.7) can have one or three solutions that represent the equilibrium conditions of the circuit. The solutions, i.e. the equilibrium conditions, can be graphically identified as the intersections between ![]() and
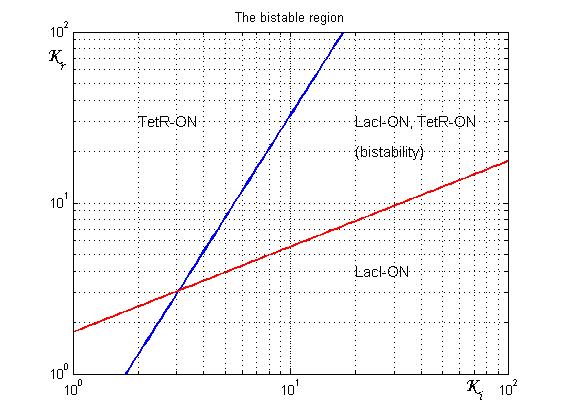
and ![]() nullclines (see Figure 2). The case of multiple equilibrium conditions (bistability case) is shown in Figure 2 panel b. TetR-ON and LacI-ON are stable equilibriums separated by the unstable one (saddle point). Due to the bistability the circuit can operate as a binary memory.
The existence of a bistability condition depends on the value of
nullclines (see Figure 2). The case of multiple equilibrium conditions (bistability case) is shown in Figure 2 panel b. TetR-ON and LacI-ON are stable equilibriums separated by the unstable one (saddle point). Due to the bistability the circuit can operate as a binary memory.
The existence of a bistability condition depends on the value of ![]() and
and ![]() parameters. If
parameters. If ![]() decrease (see Figure 2 pannel a) a saddle-node bifurcation can occur, TetR-ON equilibrium vanishes and remain only the stable equilibrium LacI-ON. The contrary occurs when
decrease (see Figure 2 pannel a) a saddle-node bifurcation can occur, TetR-ON equilibrium vanishes and remain only the stable equilibrium LacI-ON. The contrary occurs when ![]() is decreased (Figure 2 pannel c). Thus bistability is guaranteed only for a limited range of
is decreased (Figure 2 pannel c). Thus bistability is guaranteed only for a limited range of ![]() and
and ![]() values.
values.
Bifurcation analysis
Assuming that LacI-ON exists the corresponding equilibrium value of ![]() is higher than 1 (see Figure 2), then it can be assumed that
is higher than 1 (see Figure 2), then it can be assumed that ![]() and the equation (1.7) simplies to:
and the equation (1.7) simplies to:
Substituting this expression in equation (1.6) one obtain:
Then:
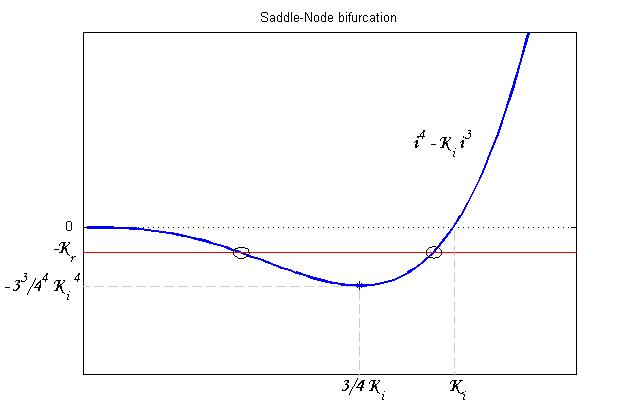
To be real the solutions of equation (1.10) it is necessary that 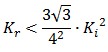 (see Figure 3). Under this condition the existence of the LacI-ON state is assured. When
(see Figure 3). Under this condition the existence of the LacI-ON state is assured. When ![]() the system undergoes a saddle-node bifurcation (LacI-ON and saddle point go in collision) and the two equilibrium points vanish.
the system undergoes a saddle-node bifurcation (LacI-ON and saddle point go in collision) and the two equilibrium points vanish.
An analogous result can be obtained for the existence of the TetR-ON state. Thus, a sufficient condition for bistability is:
Figure 4 shows the log-log plot of (1.11) and (1.12)
Procedure for Ki-index identification
The procedure will be described for LacI, analogous procedure can be applied to the TetR case. The value of ![]() -index can be identified comparing the experimental responses of the open loop and closed loop circuits:
-index can be identified comparing the experimental responses of the open loop and closed loop circuits:
- Open loop circuit
- Closed loop circuit
The LacI concentration in the open loop circuit is given by:
Thus the equilibrium condition is:
The time derivative of LacI concentration in the close loop circuit follows:
Which gives the equilibrium condition:
That can be rewritten
The affinity coefficient can consequently be derived from this expression
Inserting the (1.14) and (1.18) in the ![]() -index definition one obtain:
-index definition one obtain:
We assume that GFP is proportion to ![]() , then
, then
We introduce the ratio ![]() between the fluorescence in open loop and in closed loop:
between the fluorescence in open loop and in closed loop:
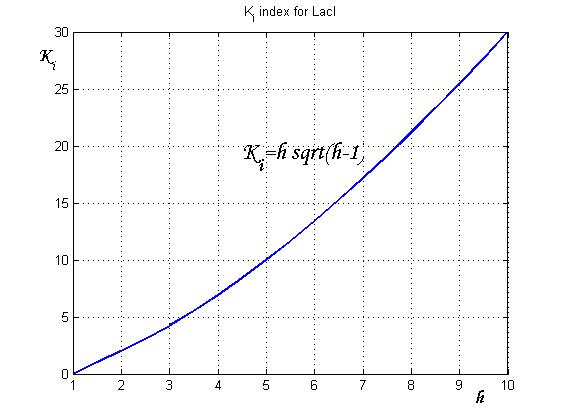
After measuring the ratio ![]() it is possible to calculate
it is possible to calculate ![]() by the curve in Figure 6 and then it is possible to establish by Figure 4 the
by the curve in Figure 6 and then it is possible to establish by Figure 4 the ![]() range that guarantees bistability. In the presence of an experimentally characterized library of regulated promoter, the procedure can be adopted to design genetic Flip-Flop with desired behaviors.
range that guarantees bistability. In the presence of an experimentally characterized library of regulated promoter, the procedure can be adopted to design genetic Flip-Flop with desired behaviors.
Numerical simulation
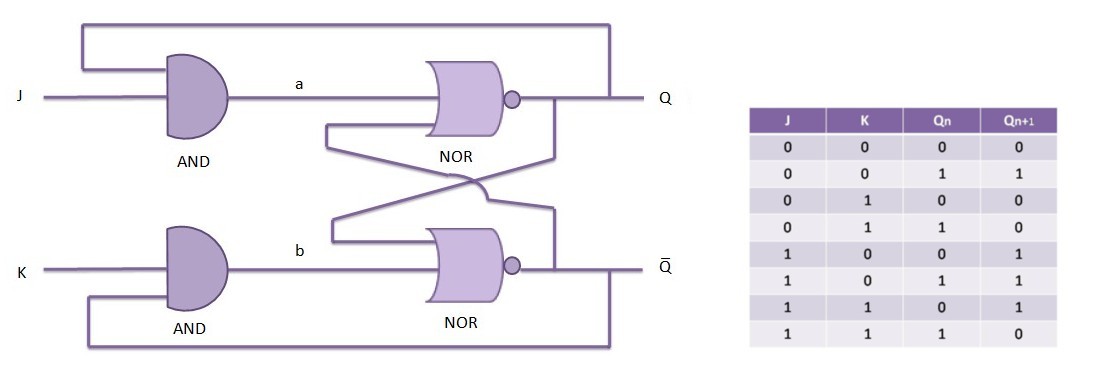
JK Flip-Flop
In digital circuits, a flip-flop is a term referring to an electronic circuit (a bistable multivibrator) that has two stable states and thereby is capable of serving as one bit of memory. Today, the term flip-flop has come to mostly denote non-transparent (clocked or edge-triggered) devices, while the simpler transparent ones are often referred to as latches; however, as this distinction is quite new, the two words are sometimes used interchangeably (see history).
A flip-flop is usually controlled by one or two control signals and/or a gate or clock signal. The output often includes the complement as well as the normal output. As flip-flops are implemented electronically, they require power and ground connections.
Flip-flops can be either simple (transparent) or clocked. Simple flip-flops can be built around a pair of cross-coupled inverting elements: vacuum tubes, bipolar transistors, field effect transistors, inverters, and inverting logic gates have all been used in practical circuits — perhaps augmented by some gating mechanism (an enable/disable input). The more advanced clocked (or non-transparent) devices are specially designed for synchronous (time-discrete) systems; such devices therefore ignores its inputs except at the transition of a dedicated clock signal (known as clocking, pulsing, or strobing). This causes the flip-flop to either change or retain its output signal based upon the values of the input signals at the transition. Some flip-flops change output on the rising edge of the clock, others on the falling edge.
Clocked flip-flops are typically implemented as master-slave devices[3] where two basic flip-flops (plus some additional logic) collaborate to make it insensitive to spikes and noise between the short clock transitions; they nevertheless also often include asynchronous clear or set inputs which may be used to change the current output independent of the clock.
Flip-flops can be further divided into types that have found common applicability in both asynchronous and clocked sequential systems: the SR ("set-reset"), D ("data" or "delay"[4]), T ("toggle"), and JK types are the common ones; all of which may be synthesized from (most) other types by a few logic gates. The behavior of a particular type can be described by what is termed the characteristic equation, which derives the "next" (i.e., after the next clock pulse) output, Qnext, in terms of the input signal(s) and/or the current output, Q.
 "
"