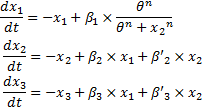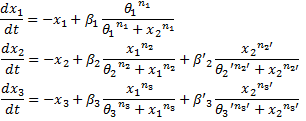Team:Paris/Modeling/BOB/Akaike
From 2008.igem.org
(Difference between revisions)
(→Experiment) |
(→Experiment) |
||
| Line 77: | Line 77: | ||
** However, since for a larger set of data System#2 minimizes the criteria, these criteria cannot decide whether a model is "better" than another one, since those criteria are arbitrary. Yet, they may help us find a better compromise between simplification and accuracy. | ** However, since for a larger set of data System#2 minimizes the criteria, these criteria cannot decide whether a model is "better" than another one, since those criteria are arbitrary. Yet, they may help us find a better compromise between simplification and accuracy. | ||
** One must be careful when building a model, since chosing the number of parameters and deciding how deep one wishes to go into detail, influences the goal and the results of a model. It is therefore important to understand that a model has to be conceived to achieve a precise aim. | ** One must be careful when building a model, since chosing the number of parameters and deciding how deep one wishes to go into detail, influences the goal and the results of a model. It is therefore important to understand that a model has to be conceived to achieve a precise aim. | ||
| - | ** Then, it is always useful to use different models, knowing that each model meets a certain demand. Here, our full model ([[Team:Paris/Modeling/ | + | ** Then, it is always useful to use different models, knowing that each model meets a certain demand. Here, our full model ([[Team:Paris/Modeling/hill_approach|APE]]) will be used to present a highly detailed overview of the processes that take place in the system. In the mean time, the [[team:Paris/Modeling/BOB|BOB]] approach is a reasonable mean to explore the system quickly and understand its ins and outs. |
Revision as of 12:39, 7 September 2008
|
What about our model?
Short introduction to the criteria
where n denotes the number of experimental values, k the number of parameters and RSS the residual sum of squares. The best fitting model is the one for which those criteria are minimized.
Experiment
System#1 : using the linear equations from our BOB approach : System#2 : using classical Hill functions :
[http://www.liebertonline.com/doi/pdf/10.1089/rej.2006.9.324 K. Kikkawa.Statistical issue of regression analysis on development of an age predictive equation. Rejuvenation research, Volume 9, n°2, 2006.]
|
||||||||||||||||||||||||||||||
 "
"