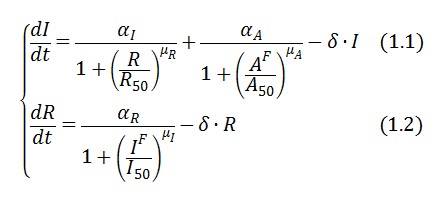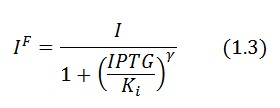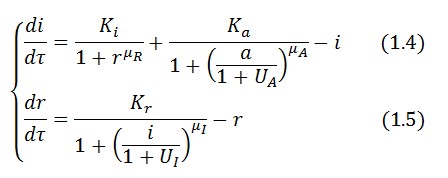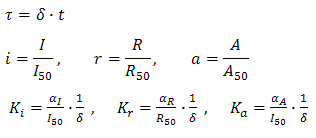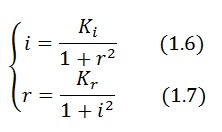Team:Bologna/Modeling
From 2008.igem.org
(→Moathematical Model based of the Flip-Flop genetic circuit) |
(→Mathematical Model based of the Flip-Flop genetic circuit) |
||
| Line 21: | Line 21: | ||
<br> | <br> | ||
| - | = Mathematical Model | + | = Mathematical Model of the Flip-Flop genetic circuit = |
<br> | <br> | ||
Revision as of 12:38, 22 October 2008
| HOME | THE PROJECT | THE TEAM | PARTS SUBMITTED TO THE REGISTRY | MODELING | NOTEBOOK | BIOSAFETY |
|---|
Contents |
Mathematical Model of the Flip-Flop genetic circuit
Model definition
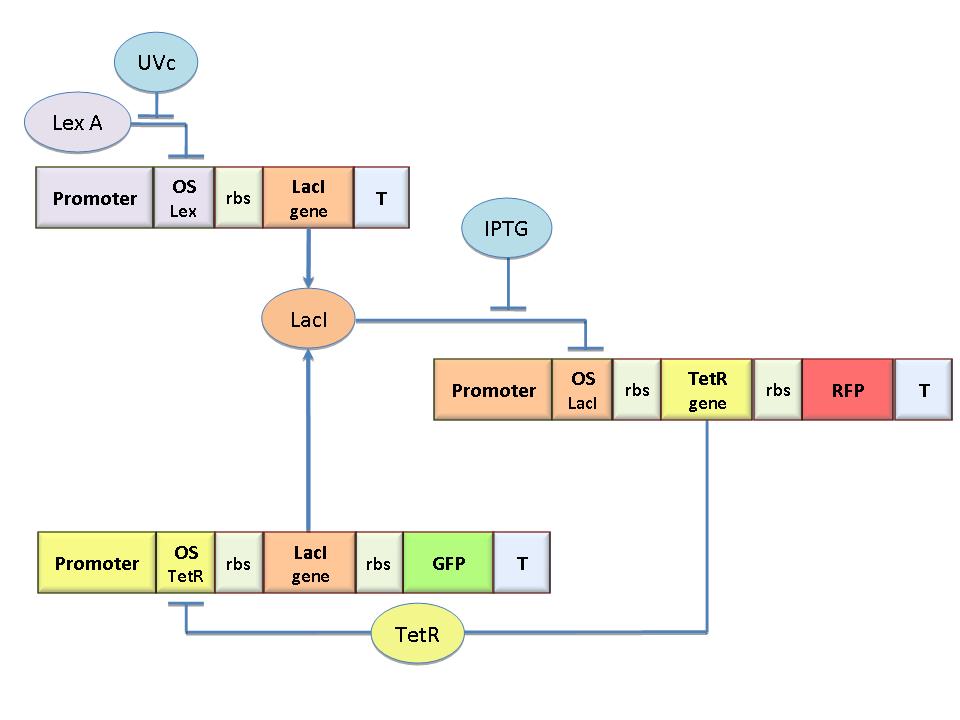
The genetic circuit in Figure 1 works as a Flip-Flop, which can switch between two different states according to the external stimuli (latch JK).
The circuit behaviour can be modeled by the following equations:
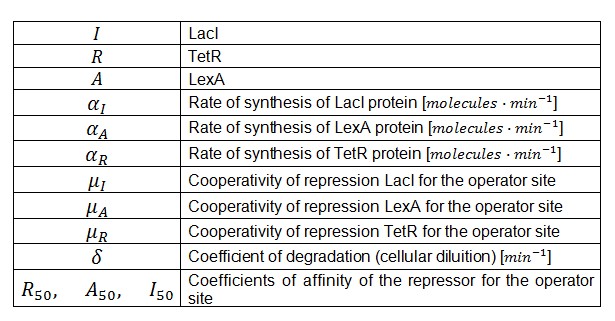
Symbols and parameters are defined in Table 1:
- A common motif in repressor proteins is the presence of a dimeric nucleotide binding site. In accordance to this general structure the cooperativity coefficients () were assumed equal to 2.
In the model we distinguish between LacI protein binded to repressor IPTG ![]() and protein free
and protein free ![]() .
.
Since ![]() and considering the law of mass action
and considering the law of mass action ![]() we can write:
we can write:
Adimensional equations
The equations (1.1) and (1.2) were modified to an adimensional form:
where:
Equibrium conditions
At equilibrium and in absence of stimuli, the adimensional concentrations of LacI (i) and TetR (r) are related by the equation:
To obtain these equations the second term in equation (1.5)was ignored (). This is justified by the high binding constant of LexA for its operator, and the consequent low production of LacI (see Figure 1).
 "
"