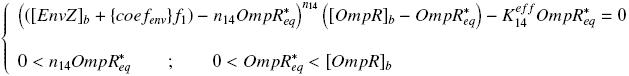Team:Paris/Modeling/f3bis
From 2008.igem.org
(Difference between revisions)
| Line 13: | Line 13: | ||
So, at steady-states, | So, at steady-states, | ||
| - | [[Image: | + | [[Image:F3b.jpg|center]] |
<br> | <br> | ||
Revision as of 14:57, 29 October 2008
|
Method & Algorithm : ƒ3bis
We have [EnvZ]real = {coefenvZ} ƒ1([aTc]i) ( and [FliA]real = {coeffliA} ƒ2([arab]i) ) but we use [aTc]i = Inv_ƒ1( [EnvZ] ) ( and [arab]i = Inv_ƒ2( [FliA] ) ) So, at steady-states,
↓ Table ↑
↓ Algorithm ↑
<Back - to "Implementation" | |
 "
"