|
(Under Construction)
Simulations and Mathematical analysis
Oscillations
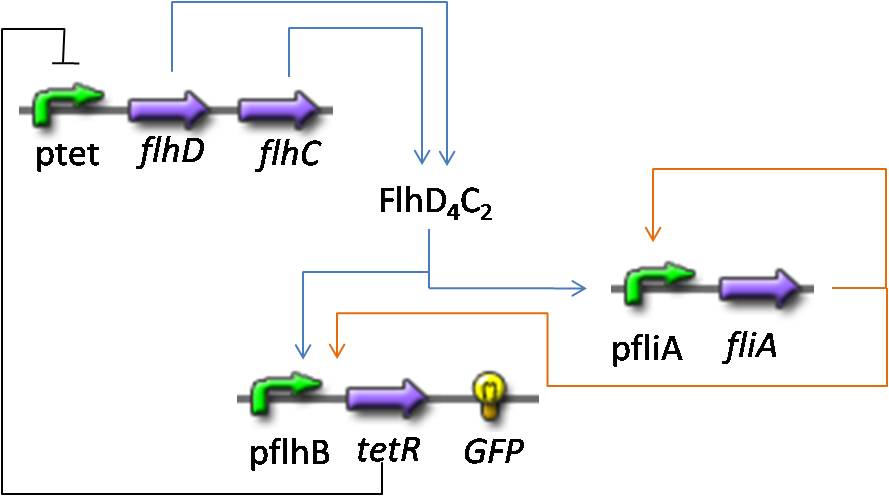
- We wanted to see if, from a mathematical point of view, it was possible for the "short" system presented above to hover.
- Here are the equations we took into account :
- The equations are normalized (thus the degradation term set to 1), as well as the parameters :
| Parameter Table
|
| Parameter
| Normalized Value
|
| βFlhDC
| 1
|
| θFlhDC
| 0.2222
|
| n
| 2
|
| βFliA
| 0.1429
|
| β'FliA
| 0.8581
|
| βLasI
| 0.2222
|
| β'LasI
| 0.7778
|
- We decided to run simulations with different values of the parameters of the Hill function. Here are plot examples with pFlhB at first :
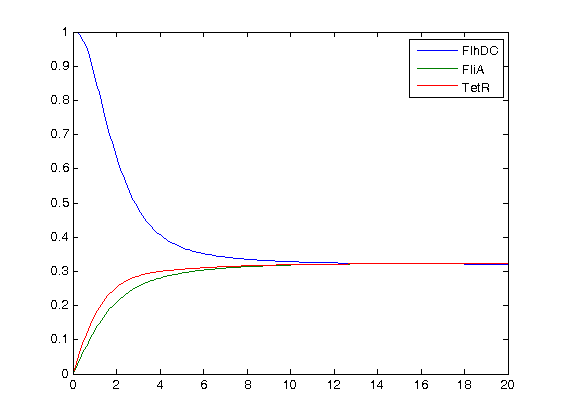 n=2 : no oscillations to be seen 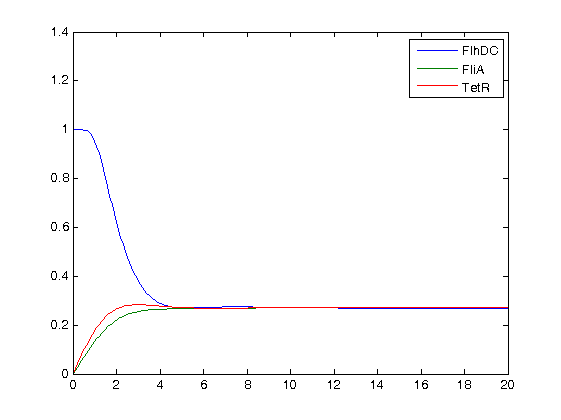 n=5 : some oscillations at the begining...  and some subdued oscillations when we zoom! 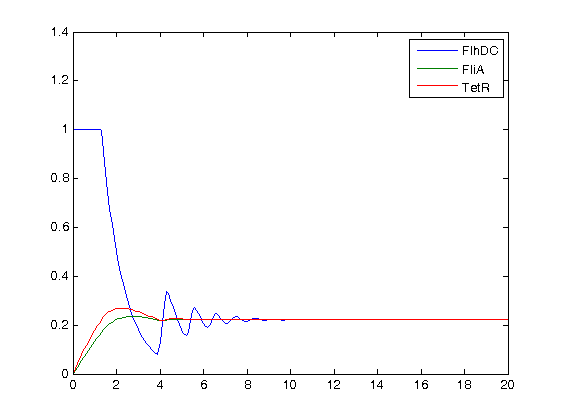 with a drastic (though non-biological) increase of n : n=300
- Then here are some plots with pFliL:
- What are the consequences of these observations?
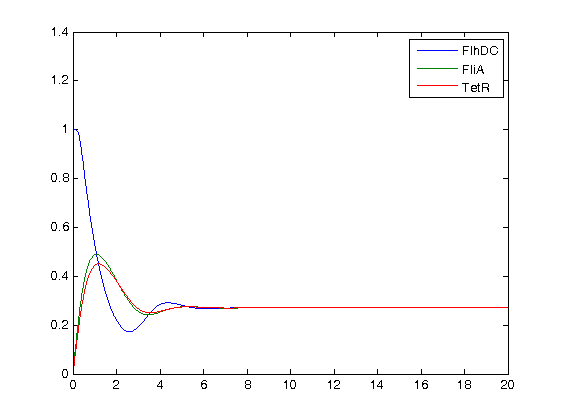
- First of all, we may see that it is hard to get stable oscillations with this short system. However, depending on the time scale, and the concentration scale (since in our models, every concentration is normalized), it is possible to sustain oscillations for some period. We may see on the zoom of the plot where we considered pFlgB and n=5 that there are non-obvious but enduring oscillations of FlhDC.
- Then, we have understood that the Hill coefficient was in that case the key parameter. In fact, while trying to change other parameters, we did not improve the results. Yet, this is a key element as far as the wet-lab is concerned.
- Furthermore, one may see that FlhDC is the source oscillator, and that the other two are following. Then, we need to put the promoter which reaction to FhlhDC is the strongest. Thus the choice of pFliL rather than pFlhB. The simulations above confirm this train of thought. Again, this is a key element to give to our wet-lab!
- To conclude, these results that are seemingly "bad news" still give us information. Indeed, we now know what gene to chose and what we can do to try to improve it.
-
- This can be confirmed by the mathematical study of the system A FAIRZE§
-
ccl :
no oscill stable, mais un peu qd mme, donc a voir sur les constantes de temps
mais intéressant: il faut choisir le premier, celui qui suit de plus pres flhDC!!! pour avoir le plus de chance d'avoir des oscillations, puisque c'est le terme de HIll qui fait osciller
puis a voir avec le systeme bio perturbé, cad que c'est pas dramatique
puis matrice
puis biocham a introduire
FIFO
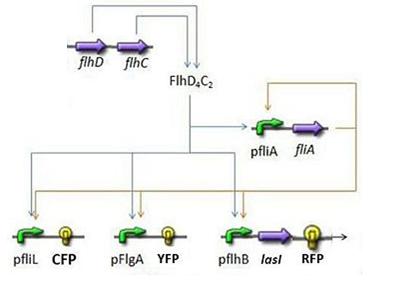
- The goal here is to present the results of the simulations we made concerning the FIFO part of the system.
Here is the system we implementated using Matlab (see the corresponding codes)
and the corresponding equations (for more detailed information see our establishment of the model).
where CFP, YFP, and RFP will be denoted below as respectively Z1,Z2 and Z3.
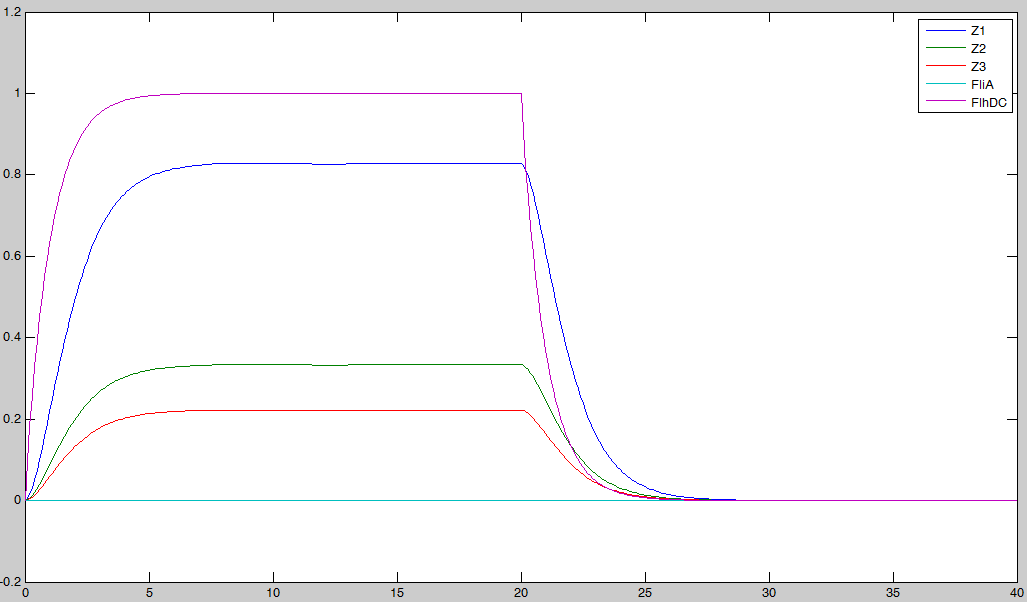
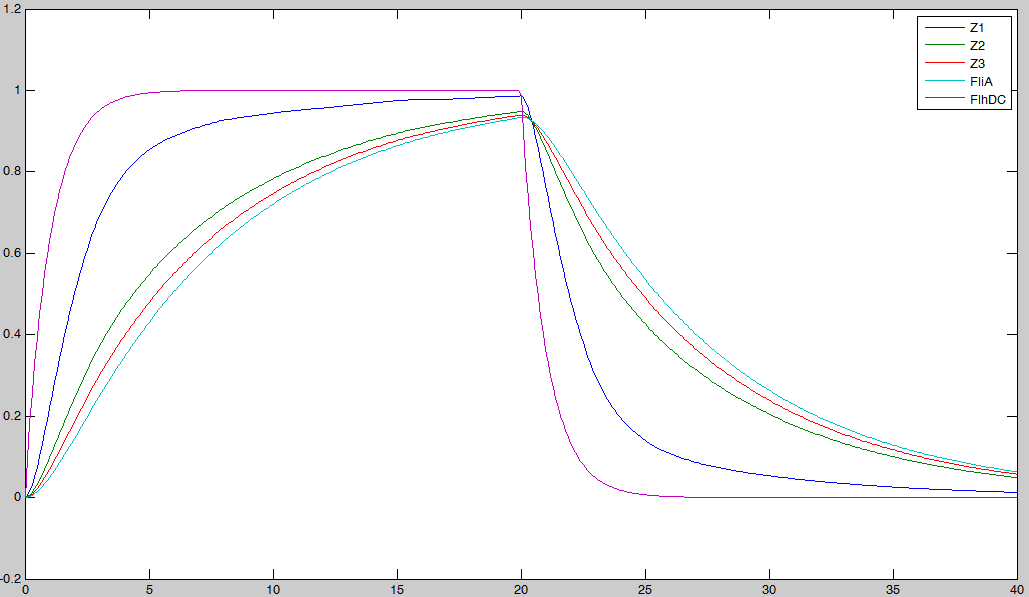
- We wanted to see if our predictions were accurate or not. We then solved the equations, forcing the behavior of FhlDC. In a first step, we imposed a constant production term of 1. Then, at a certain time, we set this production term to zero :
In fact we assumed that this behavior for FlhDC was acceptable regarding its estimated behavior in the whole system.
- We saw previously that without FliA, the FIFO would presumably not work. We then simulated a first system, where [FliA] stays to zero value.
We may see that there is a LIFO behavior rather than the FIFO we expect...
- Then, we simulated the entire system, to check if we had
- the lasting burst due to FliA (more important for Z3 than for Z2, and more important for Z2 than Z1) in the increasing phase.
- the effect of fliA which maintained the concentrations to their maximum (more important for Z3 than for Z2, and more important for Z2 than Z1) in the decreasing phase.
- We observe on these plots that the behavior is quite the one we expected, and that the FIFO is realized. FliA enables the curves to cross, and adds a delay on the genes that are most affected, with gives a better observability of the FIFO behavior.
Synchronisation
simul plsrs cells
Etude maths
|
 "
"