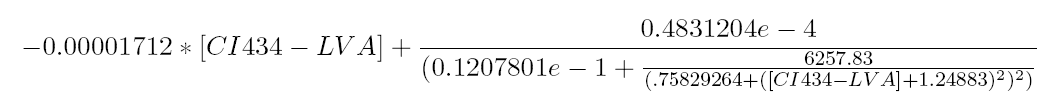Team:KULeuven/Model/Memory
From 2008.igem.org
Contents[hide] |
Memory
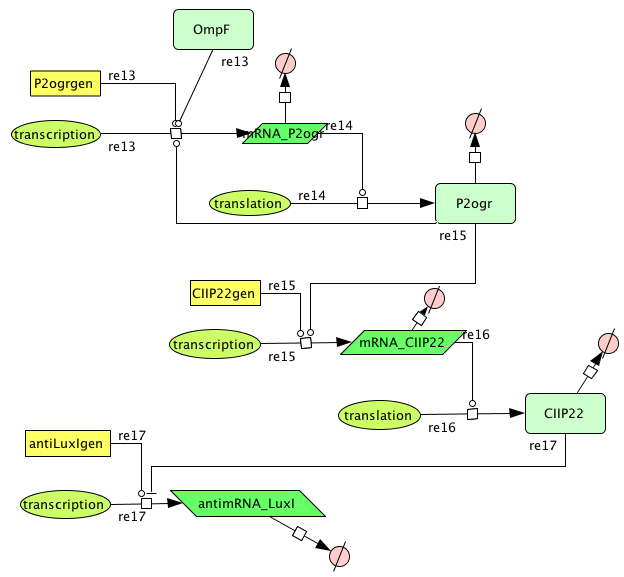
Position in the system
This system must activate the cell death system after one light pulse. As long as there is no light, there is no P2ogr, no CIIP22 and a lot of antimRNA_LuxI. The antimRNA_LuxI blocks the cell death system. When light is turned on OmpF increases. This causes P2ogr and CIIP22 to increase and antimRNA_LuxI to decrease. This activates the system. When light is turned off, the P2ogr concentration is large enough to maintain itself. This way antimRNA doesn't increase. The system stays activated.
Describing the system
ODE's
Parameters
| Name | Value | Comments | Reference |
|---|---|---|---|
| Degradation Rates | |||
| dP2ogr | 0.002265 s-1 | ||
| dRNA_P2ogr | 0.002265 s-1 | [http://www.pubmedcentral.nih.gov/picrender.fcgi?artid=124983&blobtype=pdf link] | |
| dP22CII | 0.002311 s-1 | This value is to low. The correct value is used in the final model. | [http://www.pnas.org/content/88/12/5217.abstract?sid=27806463-33af-4a78-b964-f15872433865 link] |
| dRNA_P22CII | 0,0022651 s-1 | [http://www.pubmedcentral.nih.gov/picrender.fcgi?artid=124983&blobtype=pdf link] | |
| dantimRNA_luxI | 0.0045303 s-1 | [http://www.pubmedcentral.nih.gov/picrender.fcgi?artid=124983&blobtype=pdf link] | |
| Transcription Rates | |||
| kP2ogr | 0.0125 s-1 | estimate | |
| kP22CII | 0.0125 s-1 | estimate | |
| kAntimRNA_LuxI | 0.0094 s-1 | estimate | |
| Dissociation Constants | |||
| KP2ogr | 4.2156 | Used in two reactions for activator control at the transcription of P2ogr mRNA and CIIP22 mRNA | [http://www.jbc.org/cgi/content/abstract/258/17/10536?maxtoshow=&HITS=10&hits=10&RESULTFORMAT=&fulltext=P22+c2+repressor&andorexactfulltext=and&searchid=1&FIRSTINDEX=0&sortspec=relevance&volume=258&resourcetype=HWCIT link] |
| KR0053_P22CII | 0.1099 | [http://www.jbc.org/cgi/content/abstract/258/17/10536?maxtoshow=&HITS=10&hits=10&RESULTFORMAT=&andorexactfulltext=and&searchid=1&FIRSTINDEX=0&sortspec=relevance&firstpage=10536&resourcetype=HWCIT link] | |
| Hill Cooperativity | |||
| n | 2 | Used for all reactions throughout the memory submodel using Hill kinetics | |
Models
CellDesigner (SBML file)
Matlab
Problem
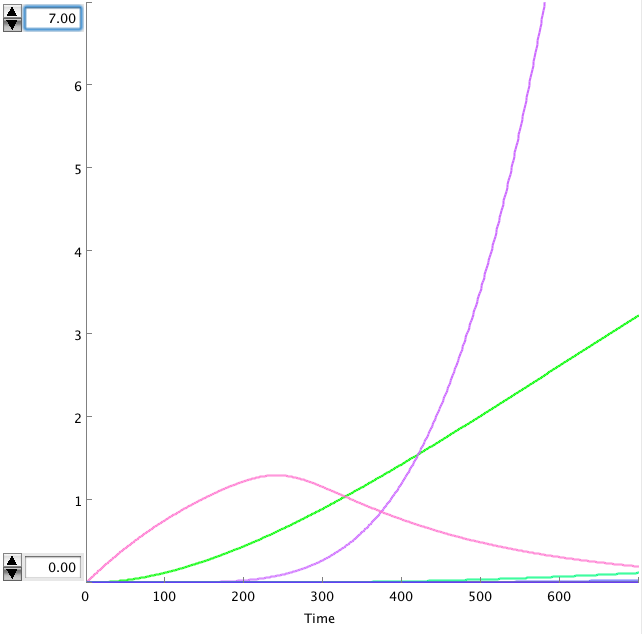
The OmpF promoter is not ideal. When there is no light the transcription rate is still 0.00005. This means that P2ogr will slowly build up, activating the system. In this case the memory is in 0-state when the stationary state isn't reached yet. The 1-state is the stationary state. So the system automatically ends up in state 1 after some time (300s). This can be seen in the figure below.
- Figure: CIIP22(purple), P2ogr(green), AntimRNA(pink).
The system can only stay in 0-state for 300 sec. This makes it completely useless.
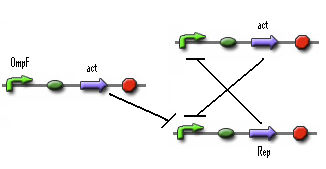
Alternative
In the previous system the 0-state isn't actively maintained. It's just 'not stationary state'. So we need to search mathematical system that has 2 stationary states. A possible solution is given below.
- Figure: Part representation of alternative system
When this system starts Rep build up because Rep represses the Act promoter better then Act represses the Rep promoter. The Rep concentration stays high and the Act stays low. This is the 0-state. When there is light, the OmpF promoter is activated and the Act concentration is increased. This represses Rep promoter. The Rep concentration decreases and the Act promoter is activated. The Act concentration keeps increasing. When the light pulse ends the Act concentration is high enough to repress the Rep promoter, Act concentration stays high and Rep concentration stays low. This is the 1-state.
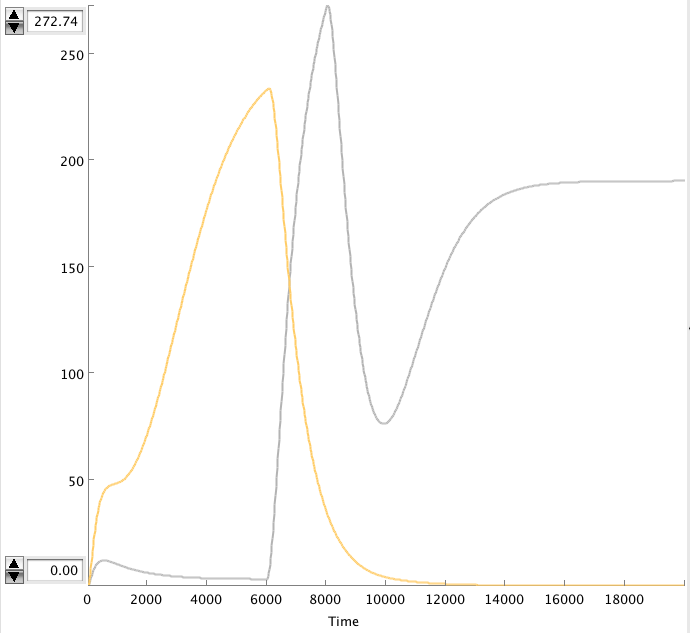
CellDesigner gives the following simulation when OmpF transcription rate changes from 0.0001 to 0.01 at t=6000 sec for 2000 sec.
- Figure: Celldesigner simulation of the alterative system. Act(grey), Rep(yellow)
The OmpF peak causes the Act concentration to rise and the Rep to decrease. The high Act concentration keeps the Rep concentration low. This causes the Act concentration to stay high.
Memory - episode 2
Position in the system
todo: this is a copy of the paragraph in the first model, it still has to be adjusted to the new model.
This system must activate the cell death system after one light pulse. As long as there is no light, there is no P2ogr, no CIIP22 and a lot of antimRNA_LuxI. The antimRNA_LuxI blocks the cell death system. When light is turned on OmpF increases. This causes P2ogr and CIIP22 to increase and antimRNA_LuxI to decrease. This activates the system. When light is turned off, the P2ogr concentration is large enough to maintain itself. This way antimRNA doesn't increase. The system stays activated.
Describing the system
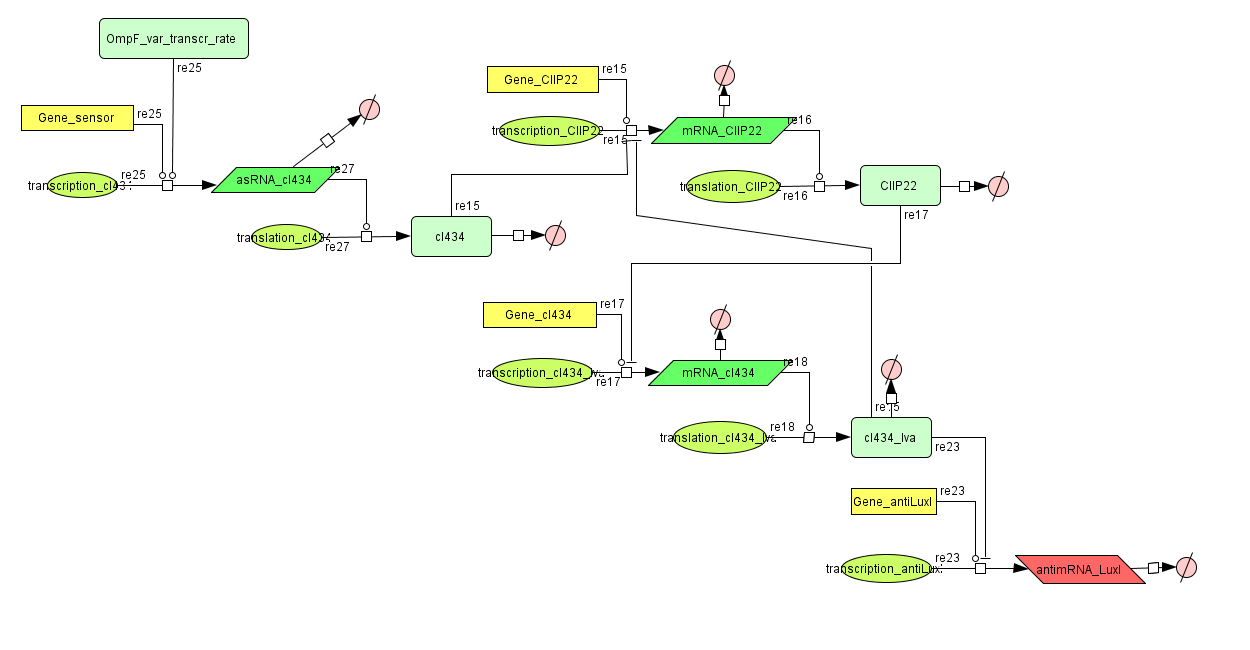
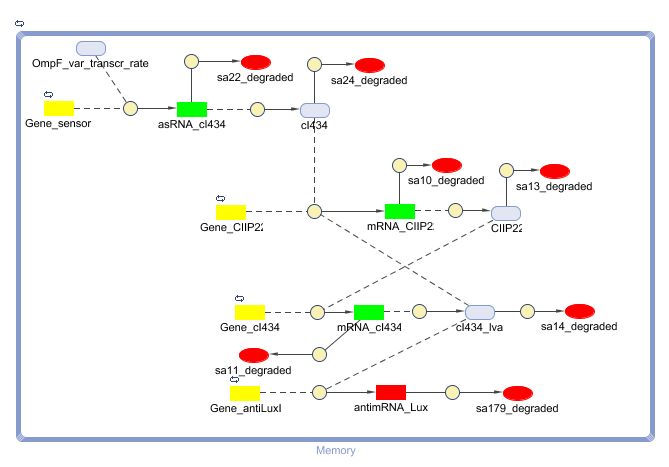
This is the same system as the alternative. The role of act is taken up by cI434 and rep by cIIP22.The output of this system is given in by RNA production that repressed the LuxI production.
ODE's
Parameters
| Name | Value | Comments | Reference |
|---|---|---|---|
| Degradation Rates | |||
| dcIIP22 | dLVA = 2.814E-4 s-1 | LVA-tag reduces lifetime to 40 minutes | [5] |
| dmRNA_cIIP22 | 0.0023104906 s-1 | [3] | |
| dcI434_LVA | dLVA = 2.814E-4 s-1 | LVA-tag reduces lifetime to 40 minutes | [5] |
| dmRNA_cI434_LVA | 0.0023104906 s-1 | [3] | |
| dcI434 | 9.627044174E-5 s-1 | no LVA tag, so longer lifetime (t1/2 = 2h) | |
| dmRNA_cI434 | 0.0023104906 s-1 | [3] | |
| dasRNA luxI | 0.00462 s-1 | estimate: because this RNA isn't translated, it degrades faster | [3] |
| dLuxI asRNA complex | 0.00462 s-1 | estimate: because this RNA isn't translated, it degrades faster | [3] |
| c2 P22 transcription (cI 434 regulated) | |||
| ktranscr | 0.0125 s-1 | estimate of maximal transcription rate, strong promoter | [10] |
| Km (cI 434) | 0.8708 | Recalculated to remove [M] dimension from Km=2E-9 [M] | [12] |
| cI 434 transcription (c2 P22 regulated) | |||
| ktranscr | 0.0040 s-1 | estimate of maximal transcription rate, weak-medium promoter | [11] |
| Km (c2 P22) | 0.1099 | Recalculated to remove [M]2 dimension from Kapp=6.8E-20[M]2 | [6] |
| TetR regulated promoter | |||
| TetR_var_transcr_rate | p(TetR) dependent | (RiboKey) between 5E-5 and 0.0125 s-1 ~ [aTc] | [4] |
| Translation rates | |||
| ktransl_cI434 | 0.0055555 s-1 | translation rate for B0033 RBS (0.01 relative efficiency) | [8] |
| ktransl_cI434_lva | 0.0388889 s-1 | translation rate for B0031 RBS (0.07 relative efficiency) | [7] |
| ktransl_cIIP22 | 0.0055555 s-1 | translation rate for B0033 RBS (0.01 relative efficiency) | [8] |
| Hill Cooperativity | |||
| n | 2 | Used for all reactions throughout the memory submodel using Hill kinetics | [2] |
| Antisense LuxI | |||
| k_complex3 | 0.00237 s-1 | rate constant for formation of asRNA - LuxI mRNA duplex | [1] |
| KmRNA_LuxI:antisense_mRNA | 4.22E-14 [M] | Dissociation constant for complex of LuxI mRNA with antisense mRNA | [1] |
Models
CellDesigner(SBML file)
Matlab (SBML file)
Simulations
Multiple simulations have been performed to see if the memory works. If we give a pulse of TetR from 5E-5 to 0.0125 for 10000 sec, we see that the memory switches from its 0-state to its 1-state (left figure): cIIP22 amount drops and the cI434 increases. The high cI434 amount will repress the RNA production. If the pulse lasts for only 1000 sec, the memory remains in its 0-state (middle figure). Simulations show the minimum time span needed to switch the memory is approximately 1300 sec. The right figure shows us that a sequence of two pulses of only 1000 sec can also make the memory switch.



Mathematical Analysis (Maple file)
The existence of the two stable states of the memory (cI434_LVA high and cIIP22 low / cI434_LVA low and cIIP22 high) can be mathematically proven.
First we define the equilibrium points of the following differential equation system:
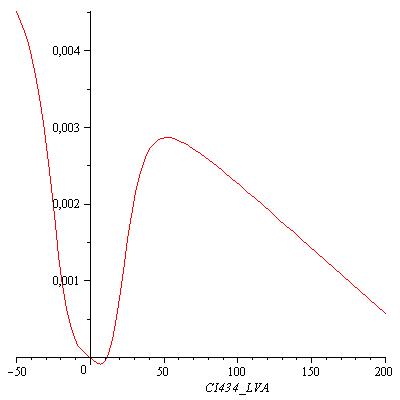
The equilibrium points are defined as the points for which all the derivatives are zero. Solving this non-linear system for [OmpF] equal to 0.00005 results in finding the roots of the equation
This equation has three real zeros ([CI434_LVA = 0.002435815407], [CI434_LVA = 11.52604711], [CI434_LVA = 233.6410112]) and two conjugated imaginary zeros ([CI434_LVA = -8.242012862+11.11131953*I], [CI434_LVA = -8.242012862-11.11131953*I]) as can be seen in the following figure:
The real roots of the system for all the variables are:
| Zero 1 | Zero 2 | Zero 3 | |
|---|---|---|---|
| [CI434] | 1.248827120 | 1.248827120 | 1.248827120 |
| [CI434-LVA] | 0.002435815407 | 11.52604711 | 233.6410112 |
| [mRNACI434-LVA] | 0.00001804584283 | 0.08539121399 | 1.730939445 |
| [CIIP22] | 34.03962262 | 0.4824866257 | 0.001433763049 |
| [mRNACIIP22] | 1.765288021 | 0.02502165991 | 0.00007435466497 |
| [asRNACI434] | 0.02164042563 | 0.02164042563 | 0.02164042563 |
The stability of the three real zeros is defined by the eigenvalues of the Jacobian of the differential equation system. This Jacobian equals
The eigenvalues for Zero 1 are all negative (-0.2334056227e-2, -0.2286362516e-2, -0.3122380843e-3, -0.2645443732e-3, -0.9627000000e-4, -0.2310490600e-2). This is also the case for Zero 3 (-0.2319019326e-2, -0.2301889325e-2, -0.2795812737e-3, -0.2967112750e-3, -0.9627000000e-4, -0.2310490600e-2). These two zero's represent the two stable states of the memory system. Zero 2 has one positive eigenvalue (0.0002015903724) and is therefore unstable.
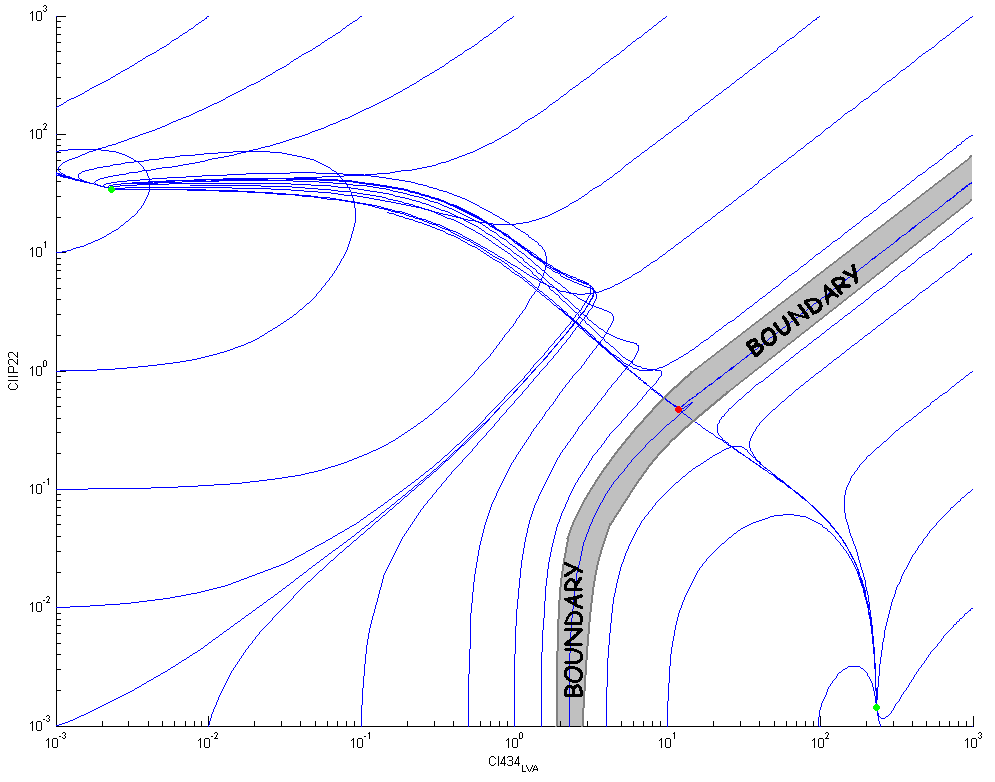
The following figure shows some trajectories in the phase plane ([CIIP22],[CI434-LVA]): there is a clear boundary between the two stable equilibrium points (the green dots) that goes through the unstable equilibrium point (the red dot). This boundary divides the two dimensional phase plane in two separate basins of attraction.
 "
"